[Toán 9-HTL] &01. Hệ thức lượng trong tam giác vuông
Hướng dẫn giải.
- Hình a
Theo định lí Pitago ta có:
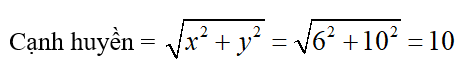
Áp dụng định lí 1 ta có:
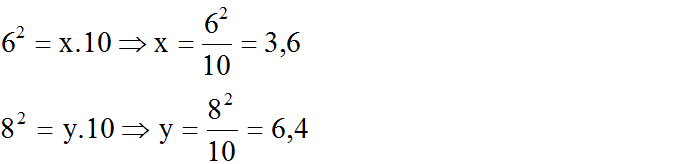
- Hình b
Áp dụng định lí 1 ta có:
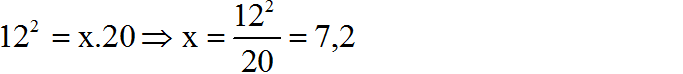
=> y = 20 - 7,2 = 12,8
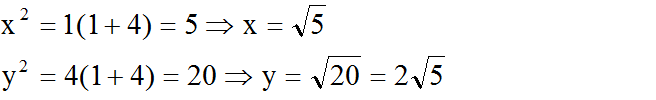
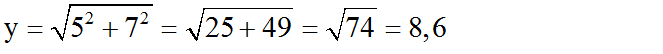
Áp dụng định lí 3 ta có:
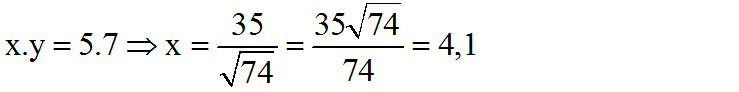
Theo định lí 1 ta có: y2 = x(1 + x) = 4(1 + 4) = 20 => y = √20 = 2√5
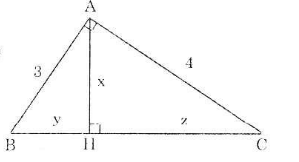
ΔABC vuông tại A có AB = 3, AC = 4 và đường cao AH như trên hình.
Theo định lí Pitago ta có:
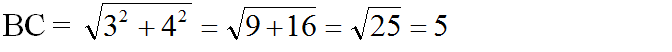
Mặt khác, AB2 = BH.BC (định lí 1)
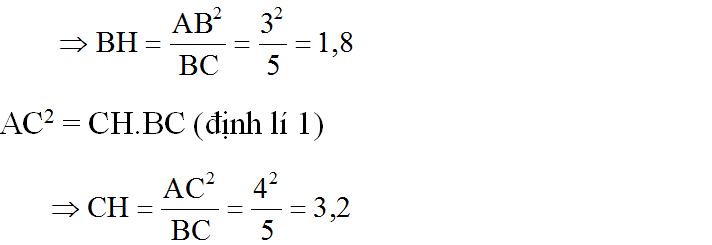
Theo định lí 3 ta có: AH.BC = AB.AC
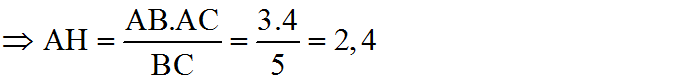
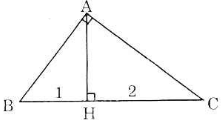
ΔABC vuông tại A và đường cao AH như trên hình.
BC = BH + HC = 1 + 2 = 3
Theo định lí 1: AB2 = BH.BC = 1.3 = 3 => AB = √3
Theo định lí 1: AC2 = HC.BC = 2.3 = 6 => AC = √6
Vậy độ dài các cạnh góc vuông của tam giác lần lượt là √3 và √6.
- Cách 1: (h.8)
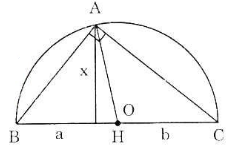
Theo cách dựng, ΔABC có đường trung tuyến AO bằng một nửa cạnh BC, do đó ΔABC vuông tại A.
Vì vậy AH2 = BH.CH hay x2 = ab
Đây chính là hệ thức (2) hay cách vẽ trên là đúng.
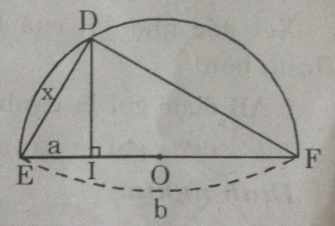
- Cách 2: (h.9)
Theo cách dựng, ΔDEF có đường trung tuyến DO bằng một nửa cạnh EF, do đó ΔDEF vuông tại D.
Vậy DE2 = EI.EF hay x2 = a.b
Đây chính là hệ thức (1) hay cách vẽ trên là đúng.
a) Theo định lí 2 ta có: x2 = 4.9 = 36 => x = 6
b) Vì đường cao chia cạnh huyền thành hai nửa bằng nhau nên nó đồng thời là đường trung tuyến. Mà trong tam giác vuông, đường tuyến bằng nửa cạnh huyền nên nên x = 2.
Theo định lí Pitago ta có:
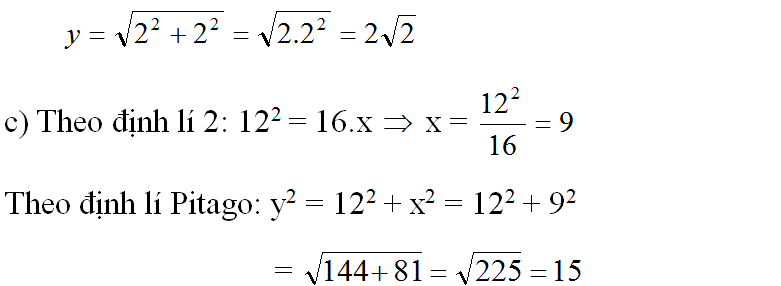

a) Xét hai tam giác vuông ADI và CDL có: AD = CD (cạnh hình vuông)
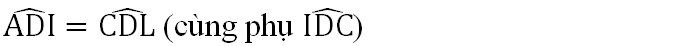
Nên ΔADI = ΔCDL (cạnh góc vuông và góc nhọn). Suy ra DI = DL hay ΔDIL cân. (đpcm)
b) Trong tam giác DKL vuông tại D với đường cao DC. Theo định lí 4, ta có:
không đổi khi I thay đổi trên cạnh AB. (đpcm)
Hướng dẫn giải.
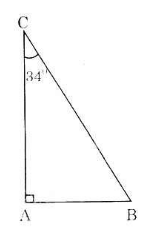
ΔABC vuông tại A có góc C = 34o. Khi đó:

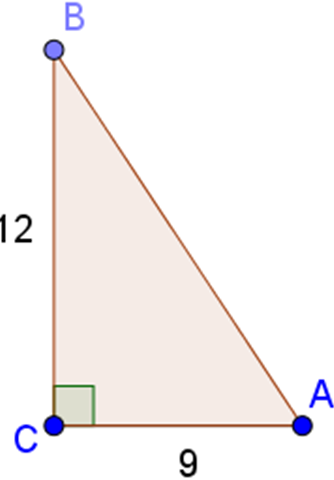
Ta có: AC = 0,9m = 9dm; BC = 1,2m = 12dm
Theo định lí Pitago, ta có:
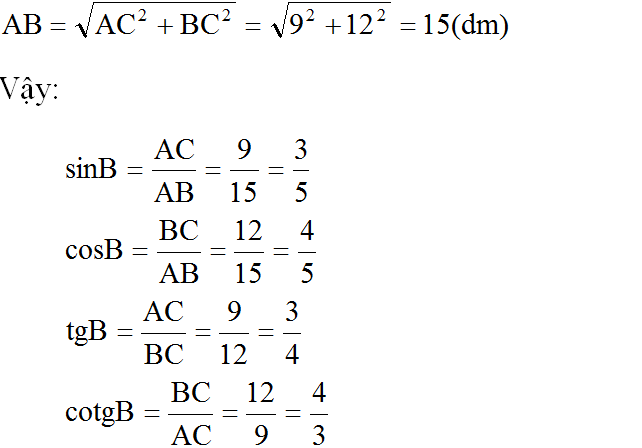
Vì ∠A và ∠B là hai góc phụ nhau nên suy ra:
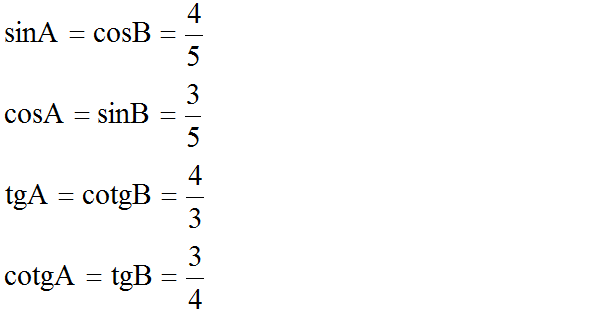
(Ghi chú: Các bạn nên đổi đơn vị như trên để việc tính toán trở nên dễ dàng hơn.)
Vì 60o + 30o = 90o nên sin60o = cos30o
Vì 75o + 15o = 90o nên cos75o = sin15o
Vì 52o30' + 37o30' = 90o nên sin 52o30'= cos37o30'
Vì 82o + 8o = 90o nên cotg82o = tg8o
Vì 80o + 10o = 90o nên tg80o = cotg10o
Hướng dẫn giải.
a)
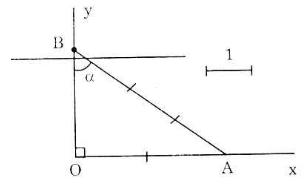
Vẽ góc vuông xOy. Trên tia Ox, lấy điểm A sao cho OA = 2cm. Lấy A làm tâm, vẽ cung tròn bán kính 3cm sao cho cung tròn này cắt tia Oy tại B. Khi đó ∠OBA = α.
Thật vậy:
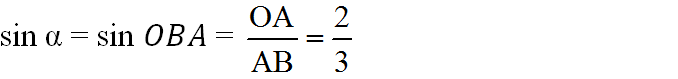
b)
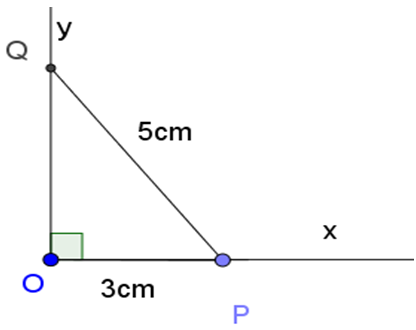
Vẽ góc vuông xOy. Trên tia Ox lấy điểm P sao cho OP = 3cm. Lấy P làm tâm, vẽ cung tròn bán kính 5cm sao cho cung này cắt tia Oy tại Q. Khi đó ∠OPQ = α.
Thật vậy:
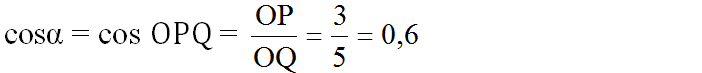
c)
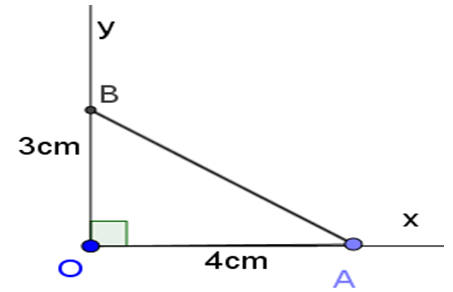
Vẽ góc vuông xOy. Trên tia Ox lấy điểm A sao cho OA = 4(cm). Trên tia Oy lấy điểm B sao cho OB = 3cm. Khi đó ∠OAB = α.
Thật vậy:

d)
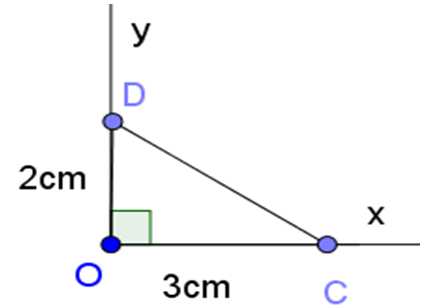
Vẽ góc vuông xOy. Trên tia Ox lấy điểm C sao cho OC = 3cm. Trên tia Oy lấy D sao cho OD = 2cm. Khi đó OCD = α.
Thật vậy:
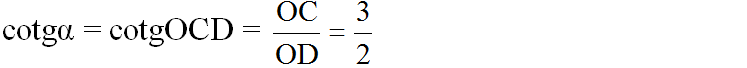
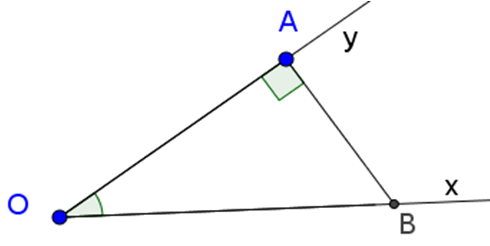
Dựng góc nhọn ∠xOy = α tùy ý.
Trên tia Ox lấy điểm B bất kì, kẻ BA ⊥ Oy (A ∈ Oy)
Theo định nghĩa tỉ số lượng giác của góc nhọn, ta có:

b) Áp dụng định lí pitago trong tam giác vuông OAB có: OB2 = OA2 + AB2
Từ đó ta có:
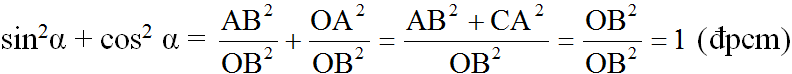

Ta có: ∠B + ∠C = 90o nên sinC = cosB = 0,8
Từ công thức sin2C + cos2C = 1 ta suy ra:
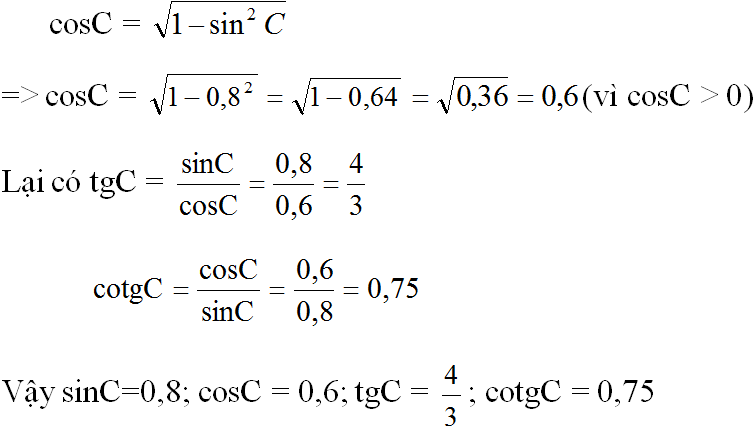
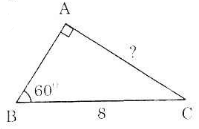
Giả sử ta có tam giác ABC như trên hình. Ta có:
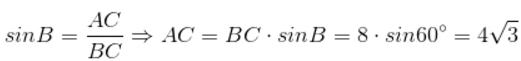
Ta có tam giác ABH là vuông cân (vì ∠B = 45o) nên AH = 20.
Áp dụng định lí Pitago trong tam giác vuông AHC có:
x2 = AH2 + HC2 = 202 + 212 = 841 => x = √841 = 29
a) Dùng bảng lượng giác: sin 40o12' ≈ 0,6455
- Cách nhấn máy tính:

b) cos52o54' ≈ 0,6032
- Cách nhấn máy tính:

c) tg63o36' ≈ 2,0145
- Cách nhấn máy tính:

d) cotg25o18' ≈ 2,1155
- Cách nhấn máy tính:

(Lưu ý: Vì trong máy tính không có nút tính cotg nên ta phải tính tg trước rồi nhấn phím nghịch đảo.)
a) Dùng bảng lượng giác sinx = 0,2368 => x ≈ 13o42'
- Cách nhấn máy tính:

b) x ≈ 51o31'
- Cách nhấn máy tính:

c) x ≈ 65o6'
- Cách nhấn máy tính:

d) x ≈ 17o6'
- Cách nhấn máy tính:

a) Dùng bảng: sin 70o13' ≈ 0,9410
- Cách nhấn máy tính:

b) cos25o32' ≈ 0,9023
- Cách nhấn máy tính:

c) tg43o10' ≈ 0,9380
- Cách nhấn máy tính:

d) cotg32o15' ≈ 1,5850
- Cách nhấn máy tính:

a) Dùng bảng sinx ≈ 0,3495 => x ≈ 20o
- Cách nhấn máy tính:

b) x ≈ 57o
- Cách nhấn máy tính:

c) x ≈ 57o
- Cách nhấn máy tính:

d) x ≈ 18o
- Cách nhấn máy tính:

a) Vì 20o < 70o nên sin 20o < sin70o (góc tăng, sin tăng)
b) Vì 25o < 63o15' nên cos25o > cos 63o15' (góc tăng, cos giảm)
c) Vì 73o20' > 45o nên tg73o20' > tg45o (góc tăng, tg tăng)
d) Vì 2o < 37o40' nên cotg 2o > cotg 37o40' (góc tăng, cotg giảm )
a)
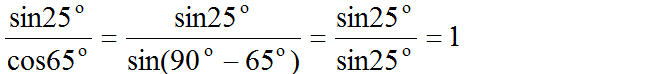
b) tg58o – cotg32o = tg58o – tg(90o – 32o) = tg58o – tg58o = 0
a) Ta có: sin 78o = cos12o; sin 47o = cos 43o
Vì 12o < 14o < 43o < 87o
nên cos 12o > cos 14o > cos 43o > cos 87o
Suy ra: cos 87o < sin47o < cos14o < sin78o
b) Ta có: cotg25o = tg65o; cotg38o = tg52o.
Vậy: cotg38o < tg62o < cotg25o < tg73o

Hướng dẫn giải.
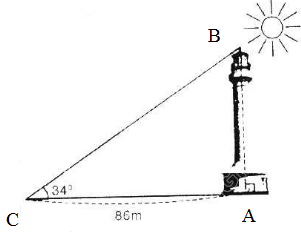
Kí hiệu đỉnh như hình vẽ. Theo hệ thức giữa các cạnh và góc của tam giác vuông, ta có:
AB = AC.tg34o = 86.tg34o ≈ 58 (m). Vậy chiều cao tòa nhà là 58m.
Giải tam giác tức là đi tìm số đo các cạnh và các góc còn lại.)
a)
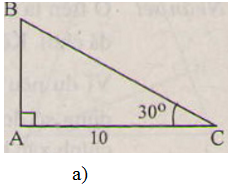
∠B = 90o - ∠C = 90o - 30o = 60o
c = b.tgC = 10.tg 30o ≈ 5,77 (cm)
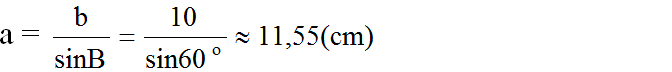
b)
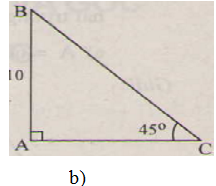
∠B = 90o - ∠C = 90o - 45o = 45o => ΔABC cân => b = c = 10 (cm)
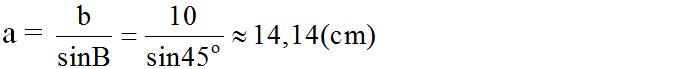
c)
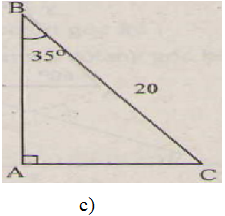
Ta có: ∠C = 90o - ∠B = 90o - 35o = 55o
b = asinB = 20.sin35o ≈ 11,47 (cm)
c = asinC = 20.sin55o ≈ 16,38 (cm)
d)

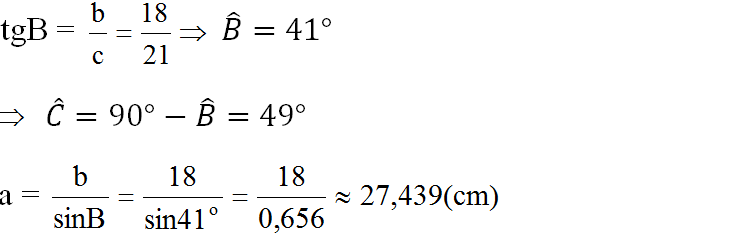
(Ghi chú: Bạn nên sử dụng các kí hiệu cạnh là a, b, c (thay vì BC, AC, AB) để đồng bộ với đề bài đã cho.
Cách để nhớ các cạnh là: cạnh nào thiếu chữ cái nào thì chữ cái đó là kí hiệu của cạnh đó. Ví dụ: cạnh AB thiếu chữ cái C nên c là kí hiệu của cạnh.
hoặc cạnh đối diện với góc nào thì đó chính là kí hiệu của cạnh. Ví dụ: cạnh đối diện với góc B là cạnh b (chính là cạnh AC))
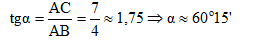
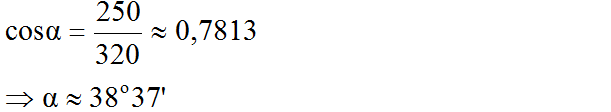

Kẻ BK ⊥ AC (K ∈ AC).
Trong tam giác vuông BKC có: ∠KBC = 90o – 30o = 60o => ∠KBA = 60o – 38o = 22o
BC = 11 (cm) => BK = 5,5 (cm) ( tính chất cạnh đối diện góc 30° trong tam giác vuông bằng nửa cạnh huyền )
Xét tam giác ABK vuông tại K:
Xét tam giác ANB vuông tại N:
=> AN = ABsinABN = 5,93.sin38° ≈ 3,65(cm)
b) Xét tam giác ANC vuông tại N:
a) AB = AC.sinC = 8.sin54o = 6,47 (cm)
b) Trong tam giác ACD, kẻ đường cao AH.
Ta có: AH = AC . sinACH = 8.sin74o = 7,69 (cm)
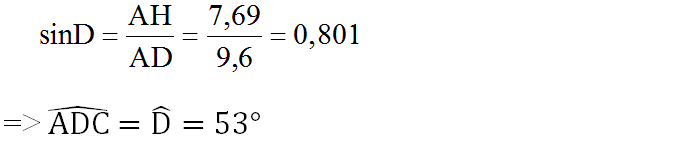
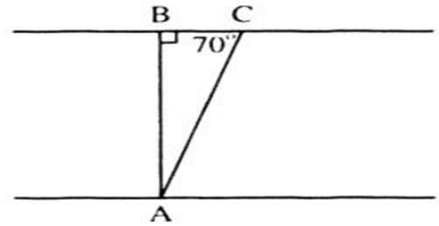
Kí hiệu như hình vẽ, trong đó:
AB là chiều rộng của khúc sông (cũng chính là đường đi của thuyền khi không có nước chảy).
AC là đoạn đường đi của chiếc thuyền (do nước chảy nên thuyền bị lệch).
Theo đề bài: v = 2km/h ; t = 5 phút = 1/12 h
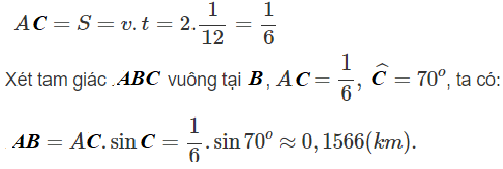
Vậy chiều rộng khúc sông là 0,1566 km = 156,6 m.
Hướng dẫn giải.
a) Chọn C
b) Chọn D
c) Chọn C vì:
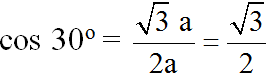
a) Chọn C
b) Chọn C sai
- Vì đẳng thức đúng phải là: cos β = sin(90o - β)

Kí hiệu góc như trên hình vẽ.
Tỉ số giữa hai cạnh góc vuông của một tam giác vuông là tg của góc nhọn này và là cotg của góc nhọn kia.
Giả sử α là góc nhọn của tam giác vuông đó.
Ta có:
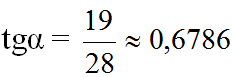
=> α ≈ 34o10' => β ≈ 90o - 34o10' = 55o50'
(Lưu ý: Bạn cũng có thể sử dụng cotg để tính, nhưng cũng sẽ cho kết quả tương tự bởi vì tính chất lượng giác của 2 góc phụ nhau.)
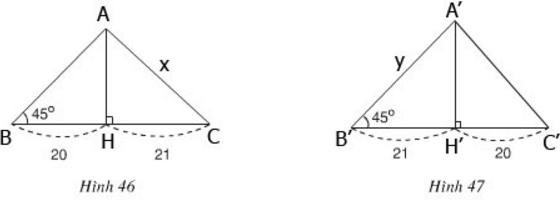
- Trường hợp hình 46: cạnh lớn trong hai cạnh còn lại được kí hiệu là x.
ΔHAB cân vì có ∠B = 45o => HA = HB = 20
Áp dụng định lí Pitago trong ΔHAC có: x2 = AC2 = HA2 + HC2 = 202 + 212 = 841
=> x = 29 hay độ dài cạnh lớn trong hai cạnh còn lại là 29.
- Trường hợp hình 47: cạnh lớn trong hai cạnh còn lại được kí hiệu là y.
ΔH'A'B' cân vì có ∠B' = 45o => H'A' = H'B' = 21
Áp dụng định lí Pitago trong ΔH'A'B' có: y2 = A'B'2 = H'A'2 + H'B'2 = 212 + 212 = 2.212
=> y = 21√2 ≈ 29,7 hay độ dài cạnh lớn trong hai cạnh còn lại là 29,7.
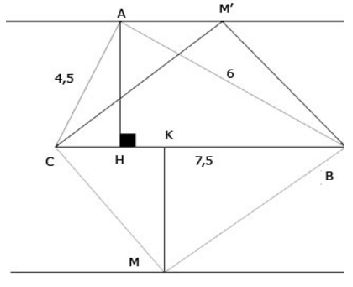
a) Ta có: AB2 + AC2 = 62 + 4,52 = 7,52 = BC2
nên tam giác ABC vuông tại A. (đpcm)
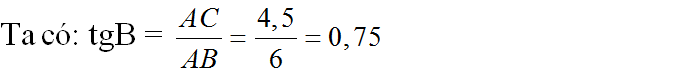
=> ∠B = 37o => ∠C = 90o - ∠B = 90o - 37o = 53o
Mặt khác trong tam giác ABC vuông tại A, ta có:

=> AH = 3,6 cm
b) Gọi khoảng cách từ M đến BC là MK. Ta có:
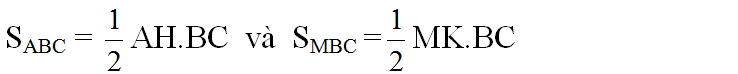
Ta thấy SMBC = SABC khi MK = AH = 3,6 cm
Do đó để SMBC = SABC thì M phải nằm trên đường thẳng song song và cách BC một khoảng là 3,6 cm (có hai đường thẳng như trên hình).
IB = IK.tg ∠IKB = IK.tg(50o + 15o) = 380.tg 65o ≈ 814 (m)
Trong tam giác vuông AIK có: IA = IK.tg ∠IKA = IK.tg 50o = 380.tg50o ≈ 452 (m)
Vậy khoảng cách giữa hai thuyền là: AB = IB – IA = 814 – 452 = 362 (m)
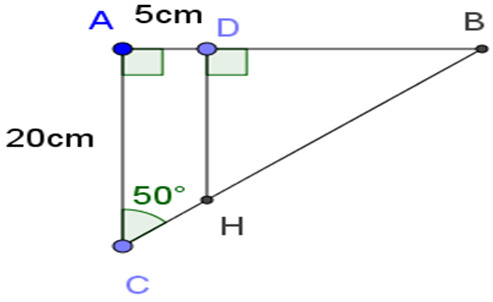
Kí hiệu như hình vẽ. Theo hệ thức giữa cạnh và góc của tam giác vuông:
Trong tam giác vuông ABC: AB = AC tan 50o = 20.tan 50o = 23,83 m
=> BD = 20tan50o - 5 = 18,83 m
Trong tam giác vuông BHD:
Vậy khoảnh cách giữa hai cọc là 24,59 m.
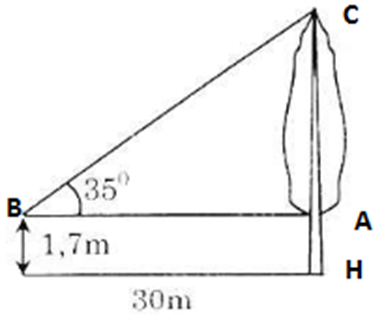
Trong tam giác vuông ABC có: AC = AB.tan35o = 30.tan35o ≈ 21 (m)
Chiều cao của cây là: CH = CA + AH ≈ 21 + 1,7 ≈ 22,7 (m)
Vậy chiều cao của cây là 22,7 (m) (hoặc = 227 dm).
(Ghi chú: Bạn cũng có thể làm tắt hơn như sau:
Chiều cao của cây là: CH = CA + AH = AC.tan35o + AH = 30.tan35o + 1,7 = 22,7 m)
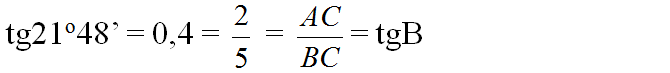
Suy ra y = 21o48' => x = 90o - y = 68o12' (x, y là hai góc phụ nhau)
Vậy x – y = 68o12' - 21o48' = 46o24'
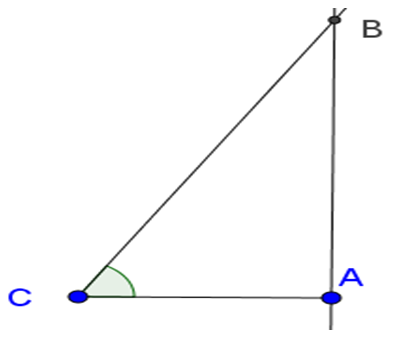
Kí hiệu như hình vẽ.
Trong tam giác vuông ABC có: AC = BC.cosC = 3.cosC
Vì phải đặt thang tạo với mặt đất một góc 60o đến 70o nên 60o ≤ ∠C ≤ 70o
=> cos 70o ≤ cosC ≤ cos 60o => 3.cos 70o ≤ 3.cosC ≤ 3.cos 60o
=> 1,03 ≤ AC ≤ 1,5
Vậy phải đặt chân thang cách tường từ 1,03 m đến 1,5 m.
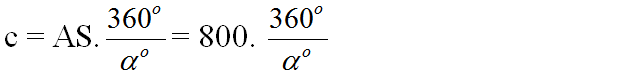
Vì các tia sáng chiếu thẳng đứng nên BC // SO do đó: ∠AOS = ∠ACB (so le trong)
Trong tam giác ABC vuông tại A có:
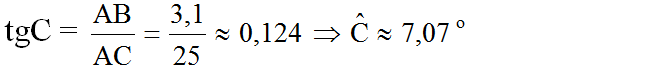
Vì ∠AOS = ∠ACB nên α = 7,07o
Vậy chu vi Trái đất là:




























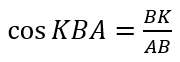
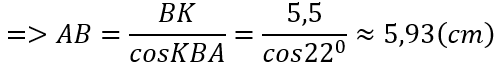
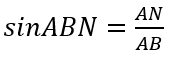
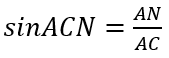
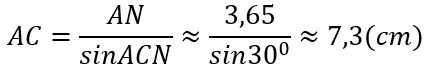







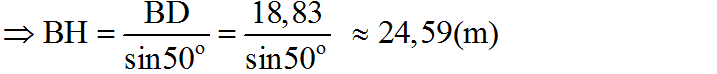


Nhận xét
Đăng nhận xét