[Toán 9-Hàm số] &01. Hàm số bậc nhất (phần 2)
Hướng dẫn giải.
a) Ta có:
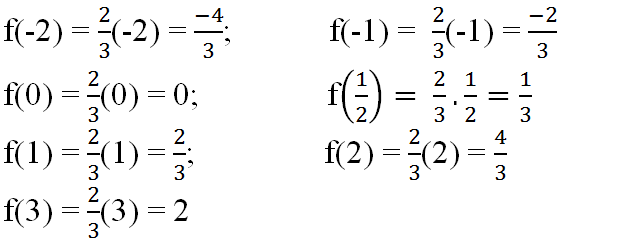
b) Ta có:
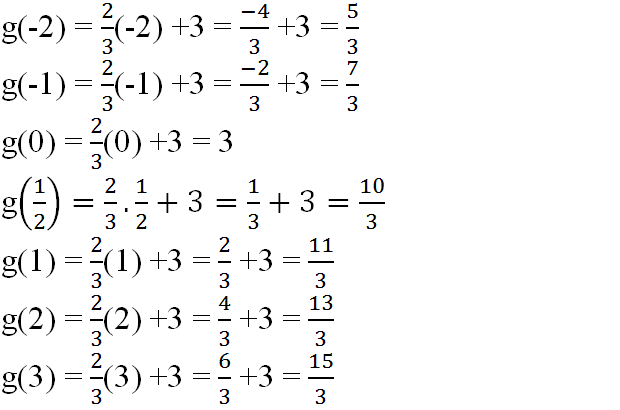
c) Từ kết quả câu a, b ta được bảng sau:
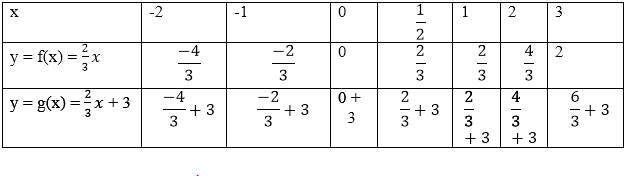
Nhận xét:
- Hai hàm số
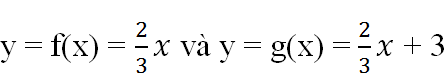
là hai hàm số đồng biến vì khi x tăng thì y cũng nhận được các giá trị tương ứng tăng lên.
- Cùng một giá trị của biến x, giá trị của hàm số y = g(x) luôn luôn lớn hơn giá trị tương ứng của hàm số y = f(x) là 3 đơn vị.
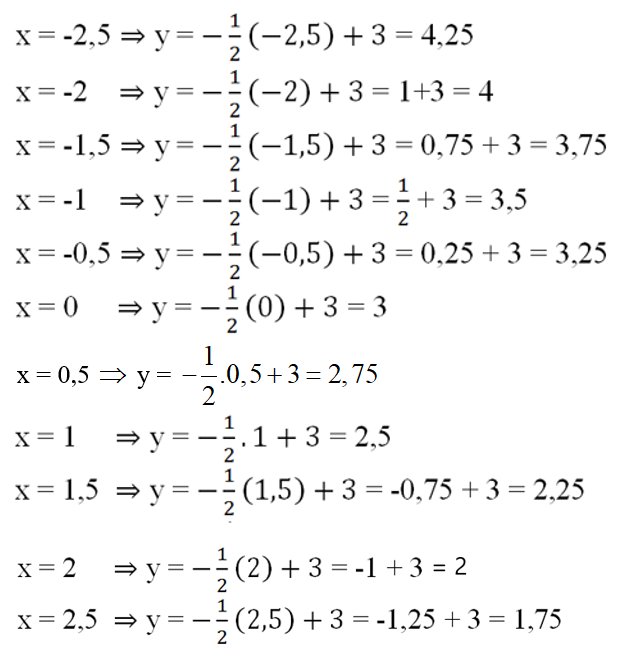
Ta được bảng sau:

b) Hàm số đã cho là hàm số nghịch biến trên R vì khi giá trị của biến x tăng lên mà giá trị tương ứng f(x) lại giảm đi.
a) - Với hàm số y = 2x
Bảng giá trị:
| x | 0 | 1 |
| y = 2x | 0 | 2 |
Đồ thị hàm số y = 2x đi qua gốc tọa độ và điểm A( 1;2)
- Với hàm số y = -2x
Bảng giá trị:
| x | 0 | 1 |
| y = -2x | 0 | -2 |
Đồ thị hàm số y = -2x đi qua gốc tọa độ và điểm B( 1; - 2)

b) - Ta có O(x1 = 0, y1 = 0) và A(x2 = 1, y2 = 2) thuộc đồ thị hàm số y = 2x, nên với x1 < x2 ta được f(x1) < f(x2). Vậy hàm số y = 2x đồng biến trên R.
- Lại có O(x1 = 0, y1 = 0) và B(x3 = 1, y3 = -2) thuộc đồ thị hàm số y = -2x, nên với x1 < x3 ta được f(x1) < f(x3). Vậy hàm số y = -2x nghịch biến trên R.
- Cách vẽ:
+ Cho x = 1 ta được y = √3.1 = √3
+ Dựng điểm A(1; √3 ). Vẽ đường thẳng qua O, A được đồ thị hàm số y = √3 x.
- Các bước vẽ đồ thị hàm số y = √3 x.
+ Dựng điểm B(1; 1). Vẽ OB ta được
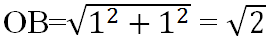
+ Dựng điểm √2 trên trục hoành Ox: vẽ cung tròn bán kính OC = √2, cắt Ox tạ điểm có hoành độ là √2.
+ Dựng điểm D(√2; 1). Vẽ OD ta được
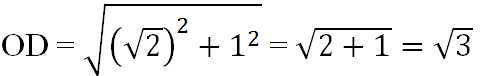
+ Dựng điểm √3 trên trục tung Ox: Vẽ cung tròn bán kính OD = √3 cắt Oy tại điểm có tung độ là √3.
+ Dựng điểm A(1; √3)
+ Vẽ đường thẳng O, A ta được đồ thị hàm số y = √3 x.
a) Vẽ đồ thị:
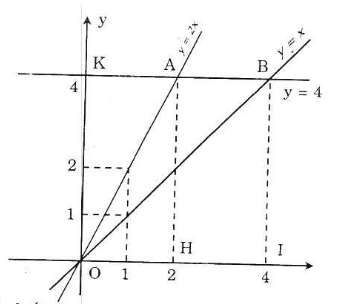
b) - Từ hình vẽ ta có: yA = yB = 4 suy ra:.
+ Hoành độ của A: 4 = 2.xA => xA = 2 (*)
+ Hoành độ của B: 4 = xB => xB = 4 => Tọa độ 2 điểm là: A(2, 4); B(4, 4)
- Tìm độ dài các cạnh của ΔOAB
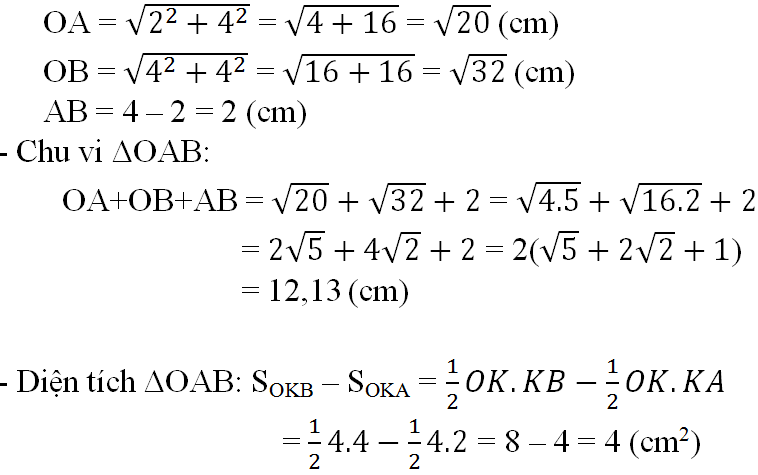
a) Sau khi tính giá trị của mỗi giá trị theo các giá trị của x đã cho ta được bảng sau:
| x | -2,5 | -2,25 | -1,5 | -1 | 0 | 1 | 1,5 | 2,25 | 2,5 |
| y = 0,5x | -1,25 | -1,125 | -0,75 | -0,5 | 0 | 0,5 | 0,75 | 1,125 | 1,25 |
| y = 0,5x + 2 | 0,75 | 0,875 | 1,25 | 1,5 | 2 | 2,5 | 2,75 | 3,125 | 3,25 |
b) Nhận xét: Cùng một giá trị của biến x, giá trị của hàm số y = 0,5x + 2 luôn luôn lớn hơn giá trị tương ứng của hàm số y = 0,5x là 2 đơn vị.
Ta có: f(x1) = 3x1 ; f( x2) = 3x2 => f(x1) - f(x2) = 3x1 - 3x2 = 3(x1 - x2) < 0 => f(x1) < f(x2)
Vậy với x1 < x2 ta được f(x1) < f(x2) nên hàm số y = 3x đồng biến trên tập hợp số thực R.
a) y = 1 – 5x là hàm số bậc nhất có a = -5, b = 1, nghịch biến vì a = -5 < 0
b) y = -0,5x là hàm số bậc nhất có a = -0,5, b = 0, nghịch biến vì a = -0,5 < 0
c) y = √2(x - 1) + √3 = √2 x + √3 - √2 là hàm số bậc nhất có a = √2, b = √3 - √2, đồng biến vì a = √2 > 0
d) y = 2x2 + 3 không phải là hàm số bậc nhất (vì số mũ của x là 2)
b) y = (m – 2)x + 3 nghịch biến khi m – 2 < 0 ⇔ m < 2. Vậy với m < 2 thì hàm số nghịch biến.
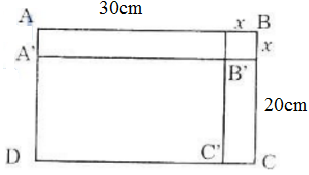
- Gọi hình chữ nhật ban đầu ABCD có kích thước AB = 30cm; BC = 20cm.
- Sau khi bớt các kích thước của hình chữ nhật đi x (cm), ta có hình chữ nhật mới là A'B'C'D' có: A'B' = 30 – x ; B'C' = 20 – x
Gọi y là chu vi của hình chữ nhật A'B'C'D', ta có:
y = 2[(30 - x) + (20 - x)] => y = 2(50 - 2x) => y = -4x + 100 (cm)
Vậy a = -0,5

a) Ta có a = 1- √5 < 0 nên hàm số đã cho nghịch biến trên R.
b) Khi x = 1 + √5 ta có: y = (1 - √5).(1 + √5) - 1 = (1 - 5) - 1 = -5
c) Khi y = √5 ta có: √5 = (1 - √5)x - 1 => √5 + 1 = (1 - √5)x
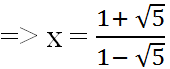
(hoặc trục căn thức ở mẫu như dưới đây:
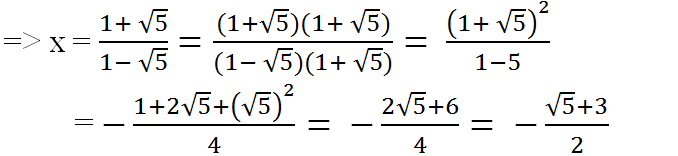
Hướng dẫn giải.
a)
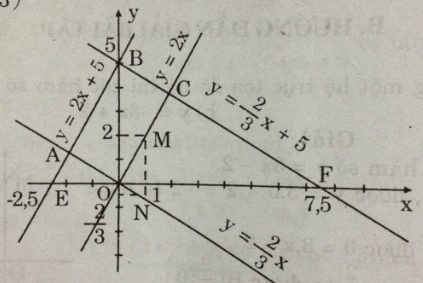
- Với hàm số y = 2x: cho x = 1 => y = 2.1 = 2 ta được M(1; 2).
- Với hàm số y = 2x + 5:
cho x = -2,5 => y = 2(-2,5) + 5 = 0 ta được E(-2,5; 0)
cho x = 0 => y = 5 ta được B(0; 5)

b) Bốn đường thẳng đã cho cắt nhau tại các điểm O, A.
Vì đường thẳng y = 2x + 5 song song với đường thẳng y = 2x,
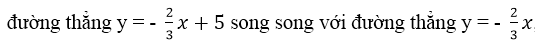
=> tứ giác OABC là hình bình hành (có hai cặp cạnh song song).
a) Vẽ đường thẳng qua O(0; 0) và điểm M(1; 1) được đồ thị hàm số y = x.
Vẽ đường thẳng qua B(0; 2) và A(-2; -2) được đồ thị hàm số y = 2x + 2.
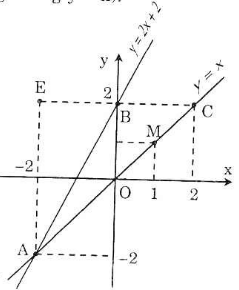
b) Hoành độ giao điểm của 2 đồ thị hàm số là nghiệm của phương trình:
2x + 2 = x => x = -2 => y = -2. Suy ra tọa độ giao điểm là A(-2; -2).
c) Qua B(0; 2) vẽ đường thẳng song song với Ox, đường thẳng này có phương trình y = 2 và cắt đường thẳng y = x tại C.
- Tọa độ điểm C:
Hoành độ giao điểm của 2 đồ thị hàm số là nghiệm của phương trình:
x = 2 => y = 2 => tọa độ C(2; 2)
- Tính diện tích tam giác ABC: (với BC là đáy, AE là chiều cao tương ứng với đáy BC)
a) - Với hàm số y = x + 1:
Cho x = 0 => y = 1 ta được M(0; 1).
Cho y = 0 => x + 1 = 0 => x = -1 ta được B(-1; 0).
Nối MB ta được đồ thị hàm số y = x + 1.
- Với hàm số y = -x + 3:
Cho x = 0 => y = 3 ta được E(0; 3).
Cho y = 0 => -x + 3 = 0 => x = 3 ta được A(3; 0).
Nối EA ta được đồ thị hàm số y = -x + 3.
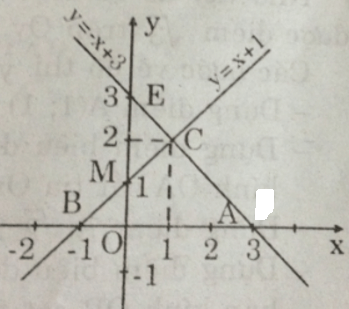
b) Từ hình vẽ ta có:
- Đường thẳng y = x + 1 cắt Ox tại B(-1; 0).
- Đường thẳng y = -x + 3 cắt Ox tại A(3; 0).
- Hoành độ giao điểm C của 2 đồ thị hàm số y = x + 1 và y = -x + 3 là nghiệm phương trình:
x + 1 = -x + 3 => x = 1 => y = 2 => Tọa độ C(1; 2)
c) Ta có: AB = 3 + 1 = 4
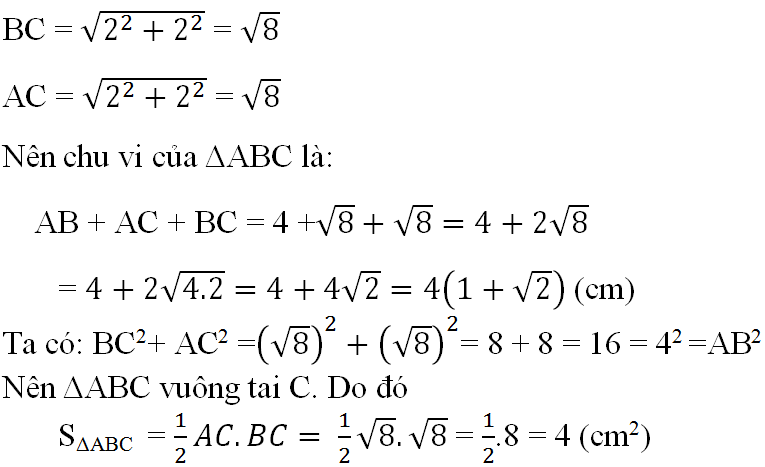
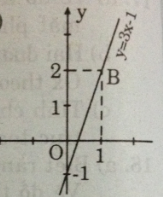
a) Thay x = 4 và y = 11 vào y = 3x + b ta được: 11 = 3.4 + b = 12 + b => b = 11 – 12 = -1
Ta được hàm số y = 3x – 1
- Cho x = 0 => y = -1 được A(0; -1)
- Cho x = 1 => y = 2 được B(1; 2).
Nối A, B ta được đồ thị hàm số y = 3x – 1.
b) Thay tọa độ điểm A(-1; 3) vào phương trình y = ax + 5 ta có:
3 = a(-1) + 5 => a = 5 – 3 = 2. Ta được hàm số y = 2x + 5.
- Cho x = -2 => y = 1 được C(-2; 1)
- Cho x = -1 => y = 3 được D(-1; 3)
Nối C, D ta được đồ thị hàm số y = 2x + 5.
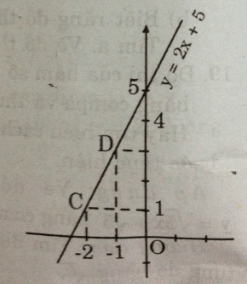
a) Cho x = 0 => y = √3 ta được (0; √3).
Cho y = 0 => √3 x + √3 = 0 => x = -1 ta được (-1; 0).
Như vậy để vẽ được đồ thị hàm số y = √3 x + √3 ta phải xác định được điểm √3 trên Oy.
Các bước vẽ đồ thị y = √3 x + √3 :
+ Dựng điểm A(1; 1) được OA = √2.
+ Dựng điểm biểu diễn √2 trên Ox: Quay một cung tâm O, bán kính OA cắt tia Ox, được điểm biểu diễn √2.
+ Dựng điểm B(√2; 1) được OB = √3.
+ Dựng điểm biểu diễn √2. Trên trục Oy: Quay một cung tâm O, bán kính OB cắt tia Oy, được điểm biểu diễn √3
+ Vẽ đường thẳng qua điểm biểu diễn √3 trên Oy và điểm biểu diễn -1 trên Ox ta được đồ thị hàm số y = √3 x + √3.
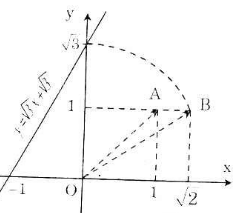
b) Áp dụng vẽ đồ thị hàm số y = √5 x + √5
- Cho x = 0 => y = √5 ta được (0; √5).
- Cho y = 0 => √5 x + √5 = 0 => x = -1 ta được (-1; 0).
Ta phải tìm điểm trên trục tung có tung độ bằng √5.
Cách vẽ:
+ Dựng điểm A(2; 1) ta được OA = √5.
+ Dựng điểm biểu diễn √5 trên trục Oy. Quay một cung tâm O, bán kính OA cắt tia Oy, được điểm biểu diễn √5. Vẽ đường thẳng qua điểm biểu diễn √5 trên Oy và điểm biểu diễn -1 trên Ox ta được đồ thị hàm số y = √5 x + √5.
- Các đường thẳng cắt nhau khi có a ≠ a'. Ta có ba cặp đường thẳng cắt nhau là:
a) y = 1,5x + 2 và b) y = x + 2 (vì có 1,5 ≠ 1)
a) y = 1,5x + 2 và c) y = 0,5x – 3 (vì có 1,5 ≠ 0,5)
a) y = 1,5x + 2 và d) y = x – 3 (vì có 1,5 ≠ 1)
...v...v......v.....v.....
- Các đường thẳng song song khi có a = a' và b ≠ b'. Ta có các cặp đường thẳng song song với nhau là:
a) y = 1,5x + 2 và e) y = 1,5x – 1 (vì có 1,5 = 1,5 và 2 ≠ -1)
b) y = x + 2 và d) y = x – 3 (vì có 1 = 1 và 2 ≠ -3)
c) y = 0,5x – 3 và g) y = 0,5x + 3 (vì có 0,5 = 0,5 và -3 ≠ 3)
Hàm số y = (2m + 1)x – 5 có các hệ số a' = 2m + 1, b' = -5
a) Vì hai hàm số là hai hàm số bậc nhất nên a và a' phải khác 0, tức là:
m ≠ 0 và 2m + 1 ≠ 0 hay
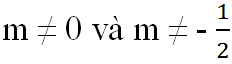
Theo đề bài ta có b ≠ b' (vì 3 ≠ -5)
Kết hợp với điều kiện trên ta thấy m = -1 là giá trị cần tìm.
b) Đồ thị của hai hàm số y = mx + 3 và y = (2m + 1)x – 5 là hai đường thẳng cắt nhau khi và chỉ khi: m ≠ 2m + 1 => m ≠ -1.
Kết hợp với điều kiện trên, ta có:

Hướng dẫn giải.
a) Theo đề bài ta có b ≠ b' (vì 3 ≠ 0)
Vậy đồ thị của hàm số y = ax + 3 song song với đường thẳng y = -2x khi và chỉ khi a = a' tức là: a = -2. Hàm số có dạng y = 2x + 3.
b) Thay x = 2, y = 7 vào hàm số y = ax + 3 ta được: 7 = a.2 + 3 => a = 2
Hàm số có dạng y = 2x + 3.
a) Đồ thị của hàm số y = 2x + b cắt trục tung tại điểm có tung độ bằng -3, nghĩa là khi x = 0 thì y = -3, do đó: -3 = 2.0 + b => b = -3
b) Đồ thị hàm số y = 2x + b đi qua điểm (1; 5), do đó ta có: 5 = 2.1 + b => b = 3
Hàm số y = (2m + 1)x + 2k – 3 có các hệ số a' = 2m + 1, b' = 2k – 3.
Hai hàm số đã cho là hàm số bậc nhất nên 2m + 1 ≠ 0
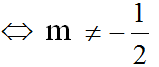
a) Hai đường thẳng cắt nhau khi a ≠ a' tức là: 2 ≠ 2m + 1 ⇔ 2m ≠ 1

b) Hai đường thẳng song song với nhau khi a = a' và b ≠ b' tức là:
2 = 2m + 1 và 3k ≠ 2k – 3

c) Hai đường thẳng trùng nhau khi a = a' và b = b' tức là:
2 = 2m + 1 và 3k = 2k – 3
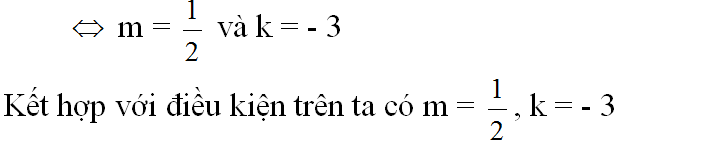
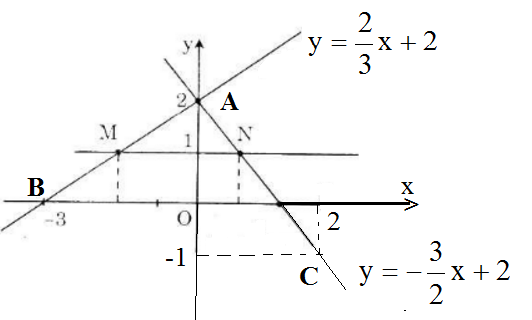

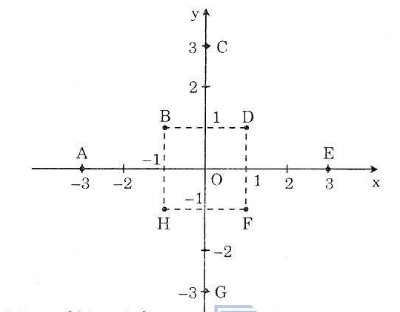
b) Điểm M có tung độ y = 1 nên hoành độ là
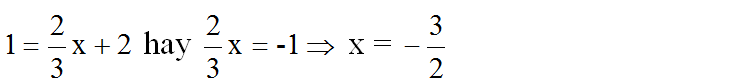
Điểm N có tung độ y = 1 nên hoành độ là
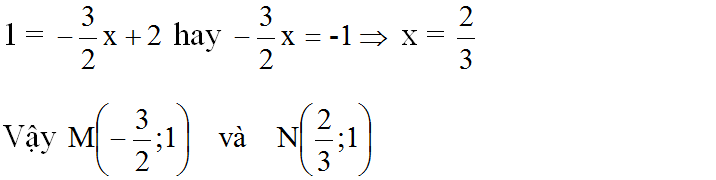
a) Đồ thị hàm số y = ax – 4 cắt đường thẳng y = 2x – 1 tại điểm có hoành độ bằng 2 nên thay x = 2 vào phương trình hoành độ giao điểm ta có: 2a – 4 = 2.2 – 1 ⇔ 2a = 7 ⇔ a = 3,5
Kết hợp với điều kiện trên ta thấy a = 3,5 là giá trị cần tìm.
b) Đồ thị hàm số y = ax – 4 cắt đường thẳng y = -3x + 2 tại điểm A có tung độ bằng 5 nên đường thẳng y = -3x + 2 đi qua điểm có tung độ bằng 5. Thay tung độ vào phương trình đường thẳng ta được hoành độ của giao điểm A là: 5 = -3x + 2 ⇔ - 3x = 3 ⇔ x = -1
Ta được A(-1; 5).
Đường thẳng y = ax – 4 cũng đi qua điểm A(-1; 5) nên ta có:
5 = a.(-1) – 4 ⇔ -a = 9 ⇔ a = -9
Kết hợp với điều kiện trên ta thấy a = -9 là giá trị cần tìm.
a) Đồ thị của hàm số đi qua điểm A(2; 6) nên:
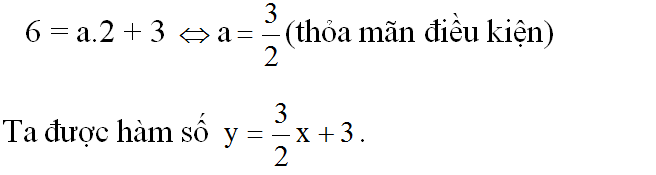
b) Vẽ đồ thị:
- Cho x = 0 thì y = 3 ta được B(0; 3).
Nối A, B ta được đồ thị hàm số
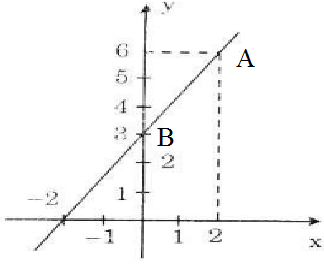
a) Vẽ đồ thị hàm số:
- Cho x = 0 thì y = 3 ta được A(0; 3)
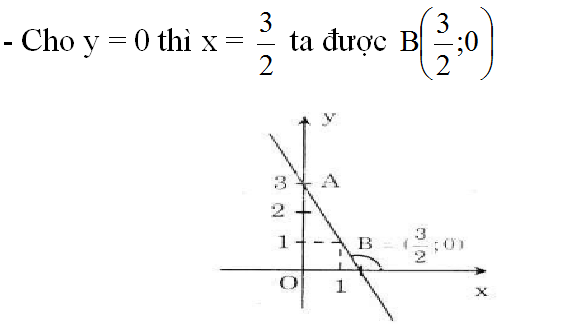
b) Gọi góc hợp bởi đường thẳng y = -2x + 3 và trục Ox là α.

Hướng dẫn giải.
a) Với a = 2 hàm số có dạng y = 2x + b.
Đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng 1,5 khi đó tung độ bằng 0 nên:
0 = 2.1,5 + b => b = -3. Vậy hàm số là y = 2x – 3
b) Với a = 3 hàm số có dạng y = 3x + b.
Đồ thị hàm số đi qua điểm (2; 2), nên ta có: 2 = 3.2 + b => b = 2 – 6 = - 4
Vậy hàm số là y = 3x – 4
c) Đường thẳng y = ax + b song song với đường thẳng y = √3 x nên a = √3 và b ≠ 0. Khi đó hàm số có dạng y = √3 x + b
Đồ thị hàm số đi qua điểm (1; √3 + 5) nên ta có: √3 + 5 = √3 . 1 + b => b = 5
Vậy hàm số là y = √3 x + 5
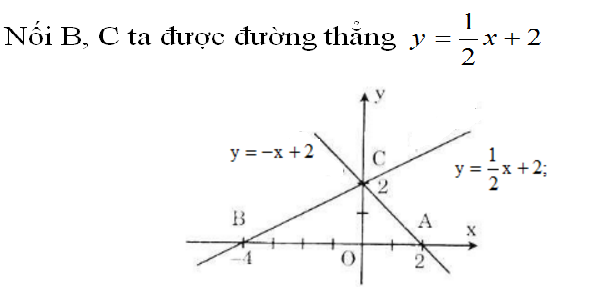
a) Vẽ đường thẳng y = -x + 2
Cho x = 0 => y = 2 được C(0; 2)
Cho y = 0 => x = 2 được A(2; 0)
Nối A, C ta được đường thẳng y = -x + 2
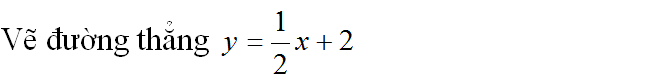
Cho x = 0 => y = 2 được C(0; 2)
Cho y = 0 => x = -4 được B(-4; 0)
c) Áp dụng định lí Pitago ta có:
a) - Với hàm số y = x + 1
Cho x = 0 y = 1 được A(0; 1)
Cho y = 0 x = -1 được B(-1; 0)
Nối A, B được đường thẳng y = x + 1
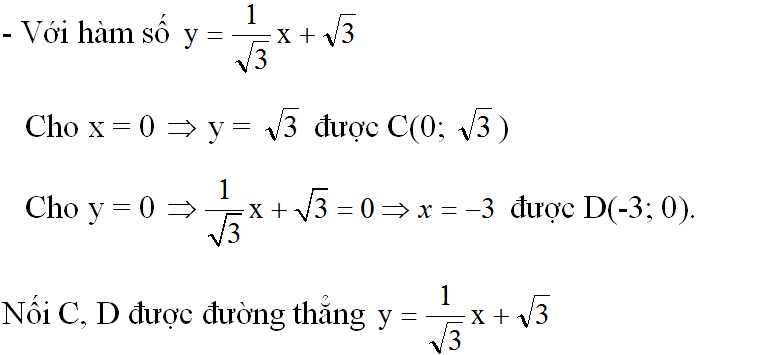
- Với hàm số y = √3 x - √3
Cho x = 0 => y = -√3 được E(0; -√3)
Cho y = 0 => x = 1 được F(1; 0).
Nối E, F được đường thẳng y = √3 x - √3
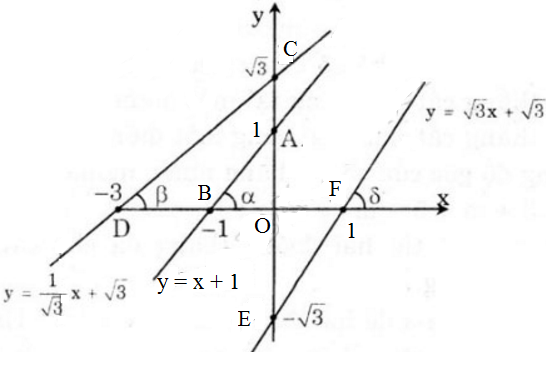
b) Ta có:
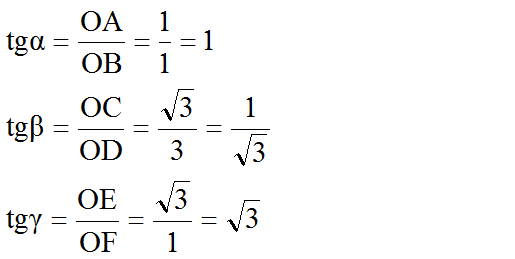
Suy ra α = 45o, β = 30o, γ = 60o
a) Hàm số y = (m – 1)x + 3 là hàm số bậc nhất đối với x khi m – 1 ≠ 0 hay m ≠ 1 (*)
Hàm số đồng biến khi m – 1 > 0 hay m > 1.
Kết hợp với điều kiện (*) ta được với m > 1 thì hàm số đồng biến.
b) Hàm số y = (5 – k)x + 1 là hàm số bậc nhất đối với x khi 5 – k ≠ 0 hay k ≠ 5 (**).
Hàm số nghịch biến khi 5 – k < 0 hay k > 5.
Kết hợp với điều kiện (**) ta được với k > 5 thì hàm số nghịch biến.
hàm số y = 2x + (3 + m) ta được tung độ: y = 3 + m
hàm số y = 3x + (5 – m) ta được tung độ: y = 5 – m
Vì cùng là tung độ của giao điểm nên: 3 + m = 5 – m => m = 1
Vậy khi m = 1 thì hai đường thẳng đã cho cắt nhau tại một điểm trên trục tung.
(Lưu ý: Điểm trên trục tung có hoành độ là 0)
Nên hai đường thẳng y = (a – 1)x + 2 và y = (3 – a)x + 1 song song với nhau khi và chỉ khi:
a – 1 = 3 – a => a = 2 (thỏa mãn a ≠ 1 và a ≠ 3)
Vậy với a = 2 thì hai đường thẳng song song với nhau.
k = 5 – k (1) và m – 2 = 4 – m (2)
Từ (1) suy ra k = 2,5 (thỏa mãn điều kiện k ≠ 0 và k ≠ 5)
Từ (2) suy ra m = 3
Vậy với k = 2,5 và m = 3 thì hai đường thẳng trùng nhau.
Hàm số y = (3 – 2k)x + 1 có các hệ số a' = 3 - 2k, b' = 1
Hai hàm số là hàm số bậc nhất nên a và a' khác 0, tức là:
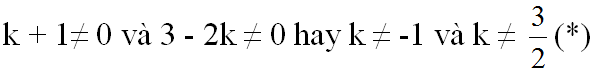
a) Theo đề bài ta có b ≠ b' (vì 3 ≠ 1)
Nên hai đường thẳng y = (k + 1)x + 3 và y = (3 – 2k)x + 1 song song với nhau khi a = a'
tức là: k + 1 = 3 – 2k
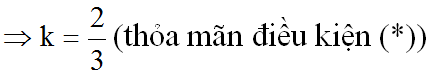
b) Hai đường thẳng y = (k + 1)x + 3 và y = (3 – 2k)x + 1 là hàm số bậc nhất nên a ≠ 0 và a' ≠ 0. Hai đường thẳng này cắt nhau khi a ≠ a' tức là:

Vậy với 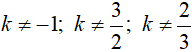
c) Do b ≠ b' (vì 3 ≠ 1) nên hai đường thẳng không thể trùng nhau với mọi giá trị k.
a) - Vẽ đồ thị hàm số y = 0,5x + 2 (1)
Cho x = 0 => y = 2 được D(0; 2)
Cho y = 0 => 0 = 0,5.x + 2 => x = -4 được A(-4; 0)
Nối A, D ta được đồ thị của (1).
- Vẽ đồ thị hàm số y = 5 – 2x (2)
Cho x = 0 => y = 5 được E(0; 5)
Cho y = 0 =>0 = 5 – 2x => x = 2,5 được B(2,5; 0)
Nối B, E ta được đồ thị của (2).
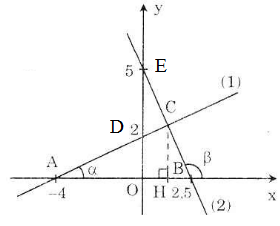
b) Ở câu a) ta tính được tọa độ của hai điểm A và B là A(-4 ; 0) và B (2,5 ; 0)
Hoành độ giao điểm C của hai đồ thị (1) và (2) là nghiệm của phương trình:
0,5 x + 2 = 5 - 2x ⇔ 0,5x + 2x = 5 – 2 ⇔ 2,5.x = 3 ⇔ x = 1,2 ⇒ y = 0,5.1,2 + 2 = 2, 6
Vậy tọa độ điểm C(1,2; 2,6).
c) AB = AO + OB = |-4| + |2,5| = 6,5 (cm)
Gọi H là hình chiếu của C trên Ox, ta có H( 1,2; 0)
Ta có: AH = AO + OH = 4 + 1,2 = 5,2
BH = BO – OH = 2,5 – 1,2 = 1,3 ; CH = 2,6
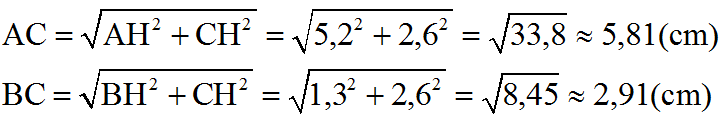
d) Gọi α là góc hợp bởi đường thẳng y = 0,5x + 2 với tia Ox.
Ta có: tgα = 0,5 => α = 26o34'
Gọi β là góc hợp bởi đường thẳng y = 5 - 2x với tia Ox
Tam giác OEB vuông tại O nên:
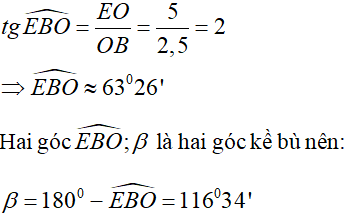
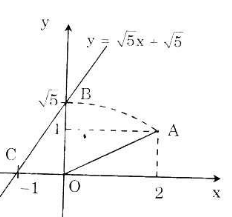
a) – Vẽ đồ thị y = 2x (1):
Cho x= 0 ⇒ y= 0 ta được O (0, 0)
Cho x= 2 ⇒ y = 4 ta được điểm (2; 4)
- Vẽ đồ thị y = 0,5x (2):
Cho x= 0 ⇒ y = 0 ta được O (0; 0)
Cho x = 4 ⇒ y = 2 ta được điểm (4; 2)
- Vẽ đồ thị y = -x + 6 (3):
Cho x = 0 ⇒ y = 6 được điểm (0; 6)
Cho y = 0 ⇒ x = 6 được điểm (6; 0)
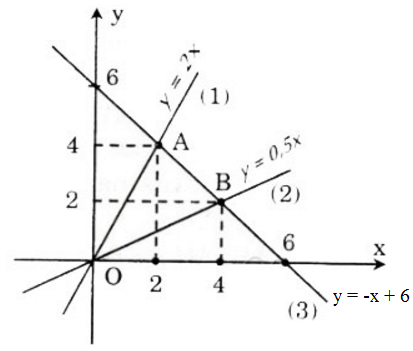
b) Theo đề bài A, B theo thứ tự là giao điểm của đường thẳng (3) với các đường thẳng (1) và (2), nên ta có:
Hoành độ giao điểm của A là nghiệm của phương trình: - x + 6 = 2x ⇒ x = 2 => y = 4
=> A(2; 4)
Hoành độ giao điểm của B là nghiệm của phương trình: - x + 6 = 0,5x ⇒ x = 4 ⇒ y = 2
⇒ B(4; 2)
c) Ta có:

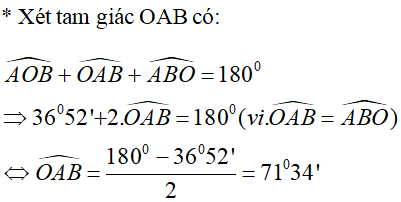













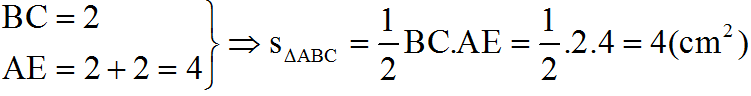












Nhận xét
Đăng nhận xét