[Toán 9-Căn bậc hai] &01. Các phép toán trên căn bậc hai
HƯỚNG DẪN GIẢI
Căn bậc hai số học của 121 là 11. Căn bậc hai của 121 là 11 và – 11.
Tương tự:
Căn bậc hai số học của 144 là 12. Căn bậc hai của 144 là 12 và -12.
Căn bậc hai số học của 169 là 13. Căn bậc hai của 169 là 13 và -13.
Căn bậc hai số học của 225 là 15. Căn bậc hai của 225 là 15 và -15.
Căn bậc hai số học của 256 là 16. Căn bậc hai của 256 là 16 và -16.
Căn bậc hai số học của 324 là 18. Căn bậc hai của 324 là 18 và -18.
Căn bậc hai số học của 361 là 19. Căn bậc hai của 361 là 19 và -19.
Căn bậc hai số học của 400 là 20. Căn bậc hai của 400 là 20 và -20.
Vì 4 > 3 nên √4 > √3 (định lí). Vậy 2 > √3
b) 6 = √36. Vì 36 < 41 nên √36 < √41. Vậy 6 < √41
c) 7 = √49. Vì 49 > 47 nên √49 > √47. Vậy 7 > √47
a) x2 = 2 => x1 = √2 và x2 = -√2
Dùng máy tính bỏ túi ta tính được: √2 ≈ 1,414213562
Kết quả làm tròn đến chữ số thập phân thứ ba là: x1 = 1,414; x2 = - 1,414
b) x2 = 3 => x1 = √3 và x2 = -√3
Dùng máy tính ta được: √3 ≈ 1,732050907
Vậy x1 = 1,732; x2 = - 1,732
c) x2 = 3,5 => x1 = √3,5 và x2 = -√3,5
Dùng máy tính ta được: √3,5 ≈ 1,870828693
Vậy x1 = 1,871; x2 = - 1,871
d) x2 = 4,12 => x1 = √4,12 và x2 = -√4,12
Dùng máy tính ta được: √4,12 ≈ 2,029778313
Vậy x1 = 2,030 ; x2 = - 2,030
a) √x = 15
Vì x ≥ 0 nên bình phương hai vế ta được: x = 152 ⇔ x = 225. Vậy x = 225
b) 2√x = 14 ⇔ √x = 7
Vì x ≥ 0 nên bình phương hai vế ta được: x = 72 ⇔ x = 49. Vậy x = 49
c) √x < √2
Vì x ≥ 0 nên bình phương hai vế ta được: x < 2. Vậy 0 ≤ x < 2
d)
Vì x ≥ 0 nên bình phương hai vế ta được: 2x < 16 ⇔ x < 8. Vậy 0 ≤ x < 8
Gọi a (m) (a > 0) là độ dài của cạnh hình vuông. Suy ra diện tích hình vuông là
SHV = a2 = 49 (m2) => a = 7 (m)
Vậy cạnh hình vuông có độ dài là 7m.
HƯỚNG DẪN GIẢI
a)
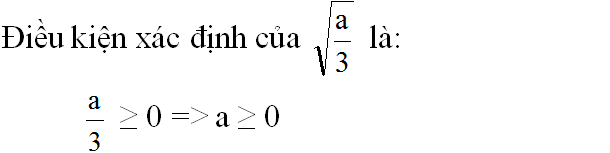
b) Điều kiện -5a ≥ 0 => a ≤ 0
c) Điều kiện 4 – a ≥ 0 => -a ≥ -4 = > a ≤ 4
d) Điều kiện 3a + 7 ≥ 0 => 3a ≥ -7

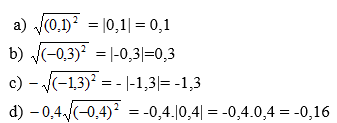
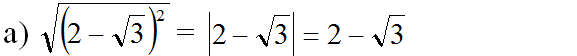
(vì 2 - √3 > 0 do 2 = √4 mà √4 > √3)
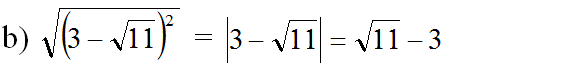
(vì √11 - 3 > 0 do 3 = √9 mà √11 > √9)
c) 2√a2 = 2|a| = 2a với a ≥ 0
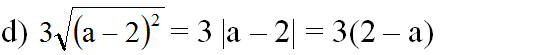
(vì a < 2 nên 2 – a > 0)
a) √x2 = 7 ⇔ |x| = 7 ⇔ x1 = 7 và x2 = -7
b) √x2 = |-8| ⇔ √x2 = 8 ⇔ |x| = 8 ⇔ x1 = 8 và x2 = -8
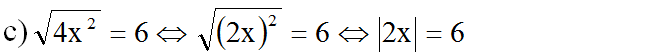
⇔ |x| = 3 ⇔ x1 = 3 và x2 = -3
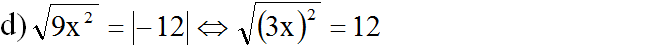
⇔ |3x| = 12 ⇔ |x| = 4 ⇔ x1 = 4 và x2 = -4
a) Ta có: VT = (√3 - 1)2 = (√3)2 - 2√3 + 1 = 3 - 2√3 + 1 = 4 - 2√3 = VP
Vậy (√3 - 1)2 = 4 - 2√3 (đpcm)
b) Theo câu a) ta có:
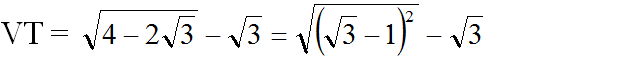
= |√3 - 1| - √3 = √3 - 1 - √3 = -1 = VP (vì √3 - 1 > 0) (đpcm)
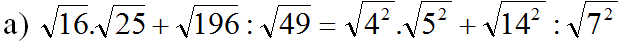
= 4.5 + 14:7 = 20 + 2 = 22
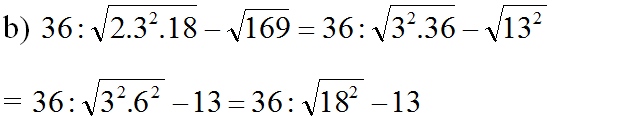
= 36 : 18 – 13 = - 11

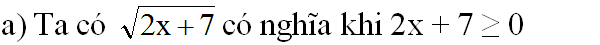
2x + 7 ≥ 0 ⇔ 2x ≥ -7
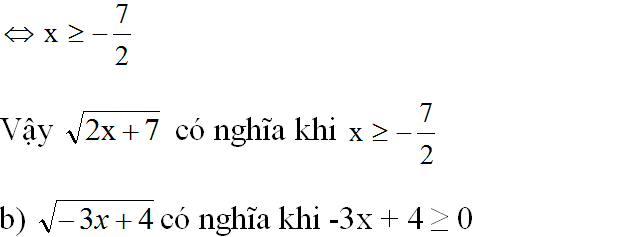
-3x + 4 ≥ 0 ⇔ -3x ≥ -4
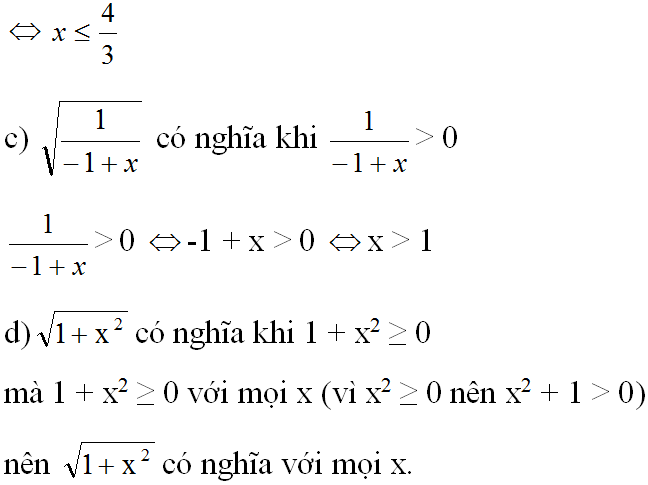
a) 2√a2 - 5a = 2|a| - 5a = -2a - 5a = -7a (do a < 0 nên |a| = -a)
b) √25a2 + 3a = 5|a| + 3a = 5a + 3a = 8a (do a ≥ 0 nên |a| = a)
c) √9a4 + 3a2 = √(3a2)2 + 3a2 = |3a2| + 3a2 = 3a2 + 3a2 = 6a2
(do a2 ≥ 0 với mọi a nên |3a2| = 3a2)
d) 5√4a6 - 3a3 = 5√(2a3)2 - 3a3 = 5|2a3| - 3a3
Với a < 0 thì |2a3| = – 2a3 nên 5|2a3| - 3a3 = -10a3 - 3a3 = -13a3
a) x2 - 3 = x2 - (√3)2 = (x - √3)(x + √3)
b) x2 - 6 = x2 - (√6)2 = (x - √6)(x + √6)
c) x2 + 2√3 x + 3 = x2 + 2√3 x + (√3)2 = (x + √3)2
d) x2 - 2√5 x + 5 = x2 - 2√5 x + (√5)2 = (x - √5)2
a) x2 – 5 = 0 ⇔ x2 = 5 ⇔ x1 = √5; x2 = -√5
Vậy phương trình có hai nghiệm x1 = √5; x2 = -√5
Cách khác: x2 – 5 = 0 ⇔ x2 – (√5)2 = 0 ⇔ (x - √5)(x + √5) = 0
hoặc x - √5 = 0 ⇔ x = √5 hoặc x + √5 = 0 ⇔ x = -√5
b) x2 – 2√11 x + 11 = 0 ⇔ x2 – 2√11 x + (√11)2 = 0 ⇔ (x - √11)2 = 0 ⇔ x - √11 = 0 ⇔ x = √11
Vậy phương trình có một nghiệm là x = √11
HƯỚNG DẪN GIẢI
Do đó, con muỗi không thể nặng bằng con voi.

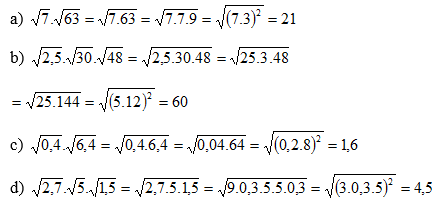

a) Ta có:

b) Ta có:
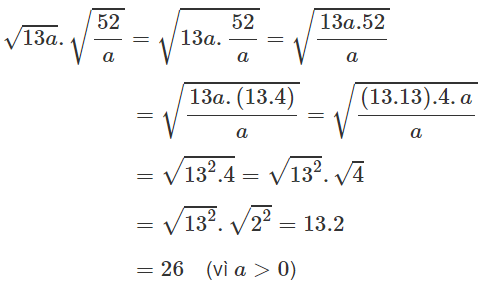
c) Do a ≥ 0 nên bài toán luôn xác định. Ta có:

(Vì a ≥ 0 nên |a| = a)
d) Ta có:
- Chọn B
- Vì ta có:
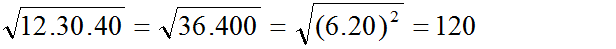
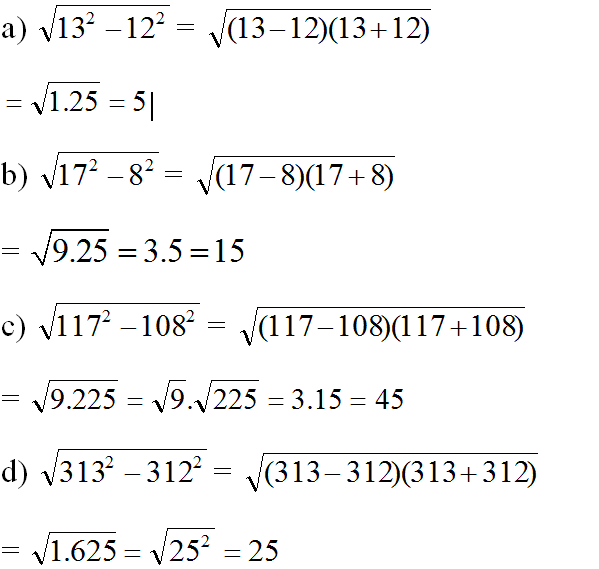

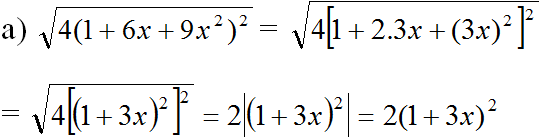
(vì (1 + 3x)2 > 0)
Thay x = √2 vào ta được: 2[1 + 3.(-√2)]2 = 2(1 - 3√2)2 = 2(1 - 6√2 + 32.2) = 2 - 12√2 + 36
= 38 - 12√2 = 38 - 12.1,414 = 38 - 16,968 = 21,032
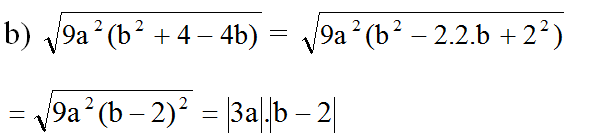
Thay a = -2, b = -√3 ta được: |3(-2)|.|-√3 - 2| = 6(√3 + 2) = 6(1,732 + 2) = 6.3,732 = 22,392
HƯỚNG DẪN GIẢI
a) √16x = 8 (điều kiện: x ≥ 0) ⇔ 16x = 82 ⇔ 16x = 64 ⇔ x = 4
(Hoặc: √16x = 8 ⇔ √16.√x = 8 ⇔ 4√x = 8 ⇔ √x = 2 ⇔ x = 4)
b) điều kiện: x ≥ 0
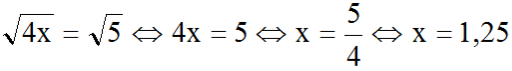
c) điều kiện: x - 1 ≥ 0 ⇔ x ≥ 1 (*)
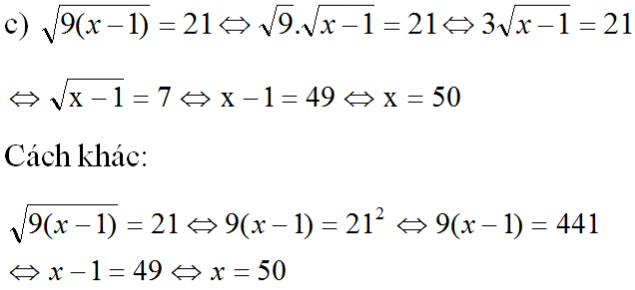
x = 50 thỏa mãn điều kiện (*) nên x = 50 là nghiệm của phương trình.
d) Vì (1 - x)2 ≥ 0 ∀x nên phương trình xác định với mọi giá trị của x.
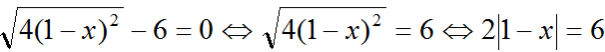
- Khi 1 – x ≥ 0 ⇔ x ≤ 1
Ta có: 2|1 – x| = 6 ⇔ 2(1 – x) = 6 ⇔ 2(1 – x) = 6 ⇔ –2x = 4 ⇔ x = –2 (nhận)
- Khi 1 – x < 0 ⇔ x > 1
Ta có: 2|1 – x| = 6 ⇔ 2[– (1 – x)] = 6 ⇔ x – 1 = 3 ⇔ x = 4 (nhận)
Vậy phương trình có hai nghiệm: x = - 2; x = 4
a) Ta có:
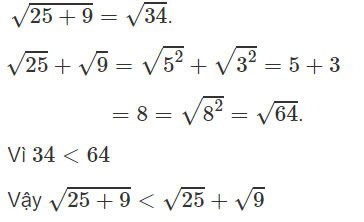
b) Ta có:
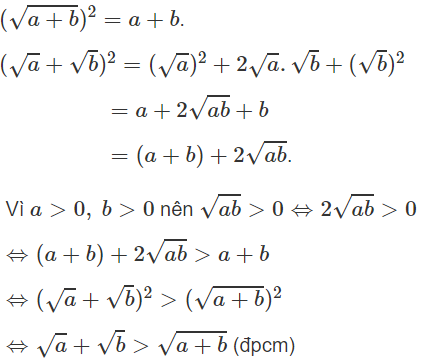
a) Ta có: 2 = √4 > √3 nên 2.2 > 2√3. Vậy √4 > 2√3
b) Ta có: √5 > √4 = 2 nên √5 > 2. Vậy -√5 < -2

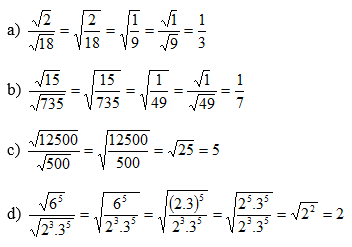
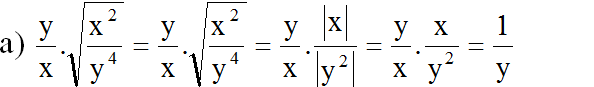
(Vì x > 0 nên |x| = x; y2 > 0 với mọi y ≠ 0)
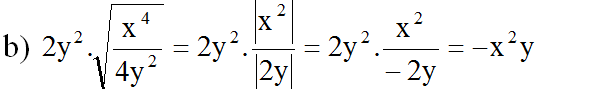
(Vì x2 ≥ 0 với mọi x; và vì y < 0 nên |2y| = – 2y)
(Vì x < 0 nên |5x| = – 5x; y > 0 nên |y3| = y3)
(Vì x2y4 = (xy2)2 > 0 với mọi x ≠ 0, y ≠ 0)
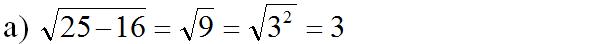
√25 - √16 = √52 - √42 = 5 - 4 = 1
Vì 3 > 1 nên


a)
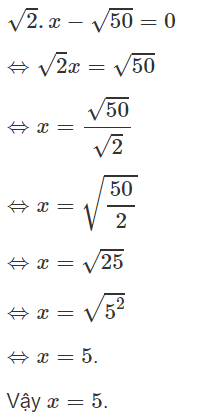
b)
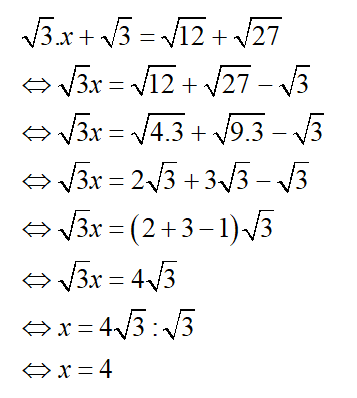
c)
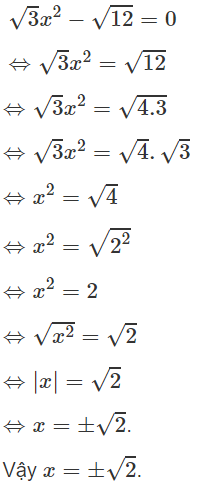
d)
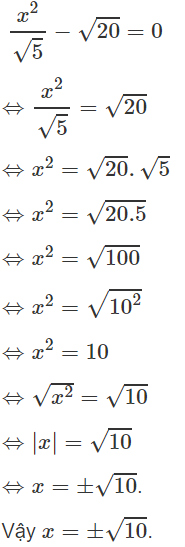
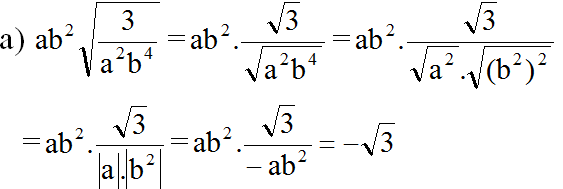
(vì a < 0 nên |a| = -a, b2 > 0 với mọi b ≠ 0 nên |b2| = b2 )
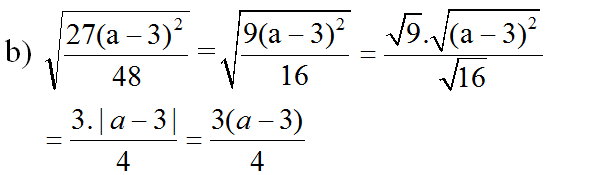
(vì a > 3 nên |a - 3| = a - 3)
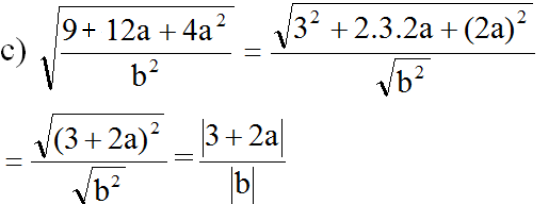
Vì b < 0 nên |b| = -b
Vì a ≥ -1,5 nên 3 + 2a ≥ 0. Do đó: |3 + 2a| = 3 + 2a
Vậy:
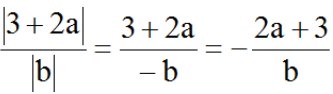

(vì a < b < 0 và b < 0 nên |a - b| = -(a - b), ab > 0)
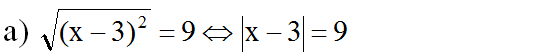
- Với x ≥ 3 thì |x - 3| = x - 3 nên ta được: x - 3 = 9 ⇔ x = 12
- Với x < 3 thì |x - 3| = 3 - x nên ta được: 3 - x = 9 ⇔ x = -6
Vậy phương trình có hai nghiệm: x = 12; x = -6
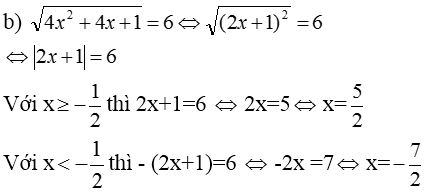
a) Đúng, vì √0,0001 = √0,012 = 0,01
b) Sai, vì vế phải không có nghĩa. (Lưu ý: √A có nghĩa khi A ≥ 0)
c) Đúng, vì 7 = √72 = √49 > √39
6 = √62 = √36 < √39
d) Đúng, vì 4 - √13 = √42 - √13 = √16 - √13 > 0
Do đó: (4 - √13).2x < √3(4 - √13) (giản ước hai vế với (4 - √13)) ⇔ 2x < √3
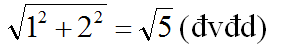
Tứ giác MNPQ là hình thoi có bốn cạnh bằng nhau.
Mỗi đường chéo của tứ giác MNPQ là đường chéo của hình chữ nhật do ba ô vuông ghép lại, nên giác NMPQ có hai đường chéo bằng nhau và bằng

Hình thoi MNPQ là hình vuông có hai đường chéo bằng nhau.
Diện tích hình vuông MNPQ: S = (√5)2 = 5 (cm2)
HƯỚNG DẪN GIẢI
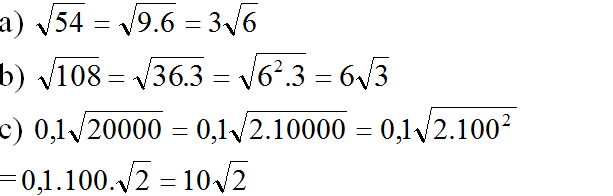
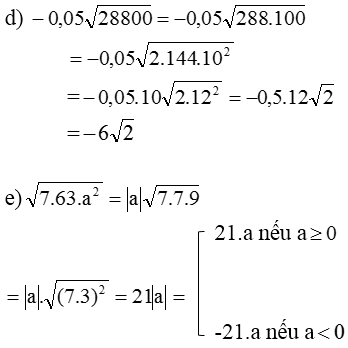
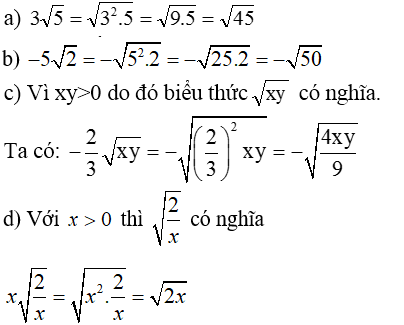
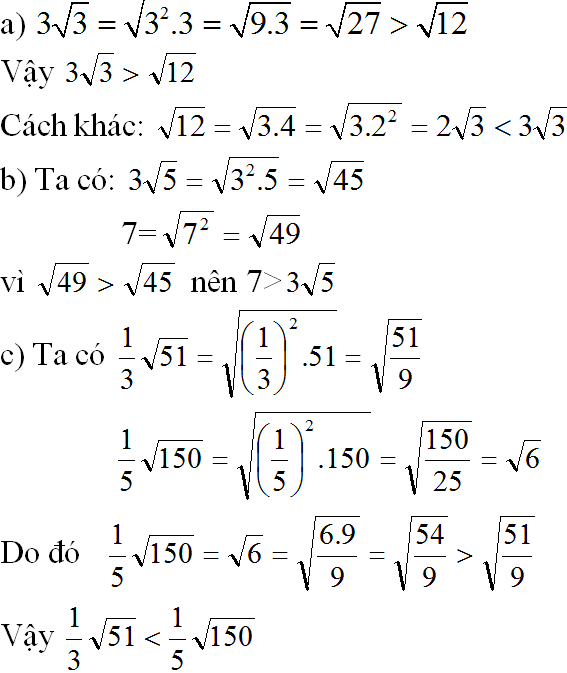

a) Với x ≥ 0 thì √3x có nghĩa. Ta có:
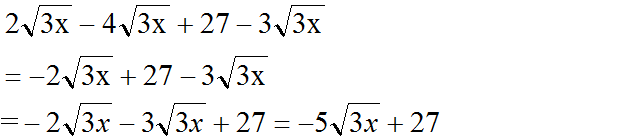
b) Với x ≥ 0 thì √2x có nghĩa. Ta có:
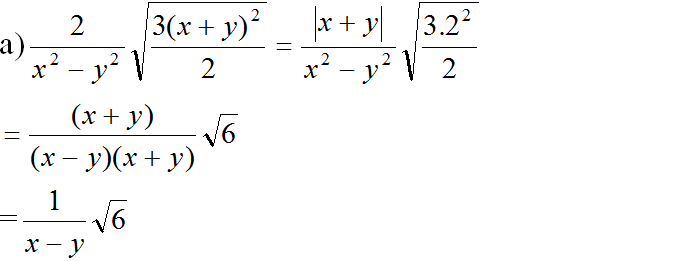
(có |x + y| = x + y do x + y > 0 vì x ≥ 0, y ≥ 0 và x ≠ y)
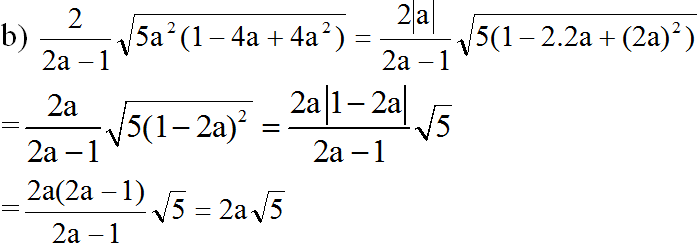
(có |a| = a do a > 0,5 và |1 - 2a| = 2a - 1 vì 2a - 1 > 0 do a > 0,5)

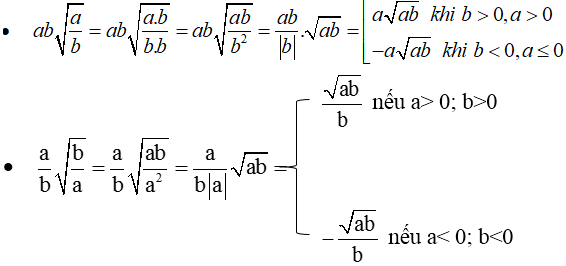

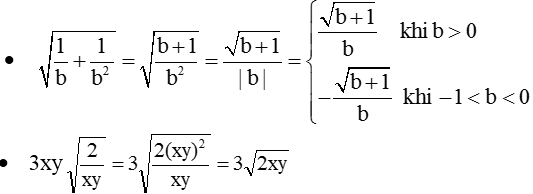
(do xy > 0 (gt) nên đưa thừa số xy vào trong căn để khử mẫu)

Cách khác:
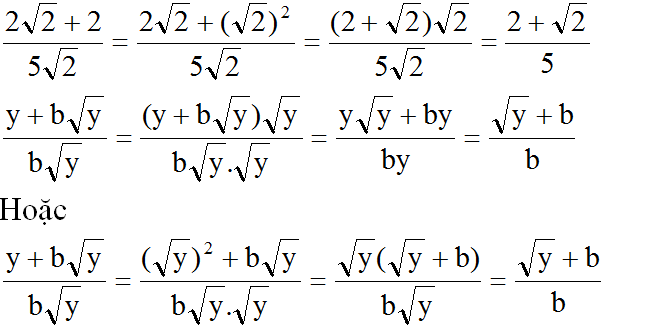
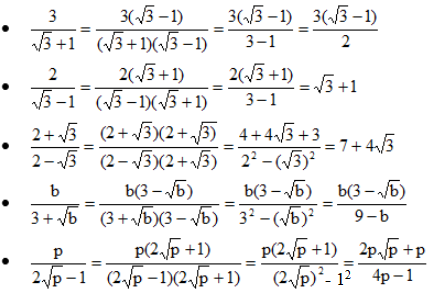
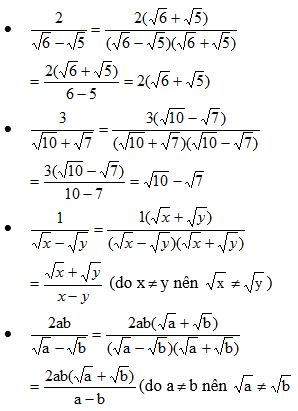

d)
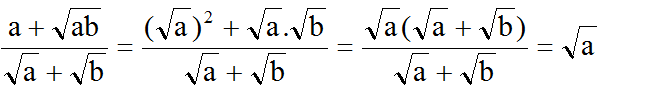
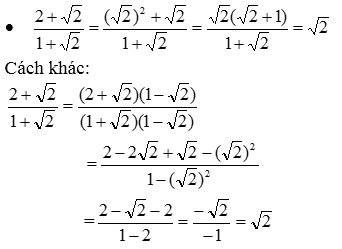
Nhận xét: Cách làm thứ nhật (nhận dạng tử có thể phân tích thành nhân tử để rút gọn nhân tử đó với mẫu thích hợp hơn cách làm thứ hai (trục căn thức ở mẫu rồi thu gọn). Vì trục căn thức ở mẫu rồi rút gọn sẽ thêm nhiều phép nhân.
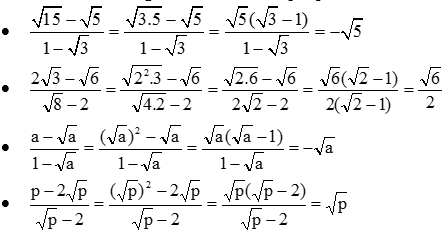
a) ab + b√a + √a + 1 = [(√a)2b + b√a] + (√a + 1) = b√a(√a + 1) + (√a + 1) = (√a + 1)(b√a + 1)

= (√x - √y)(√x + √y)2 = (√x - √y)(√x + √y)(√x + √y) = (x - y)(√x + √y)
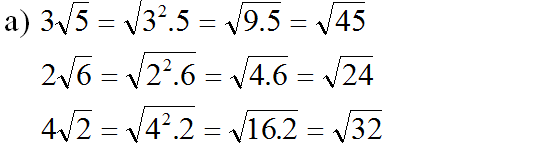
Vì √24 < √29 < √32 < √45. Nên ta sắp xếp được: 2√6 < √29 < 4√2 < 3√5

Vì √38 < √56 < √63 < √72. Nên ta sắp xếp được: √38 < 2√14 < 3√7 < 6√2
- Chọn D
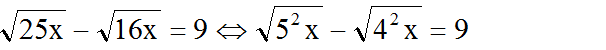
⇔ 5√x - 4√x = 9 ⇔ √x = 9 ⇔ x = 81
HƯỚNG DẪN GIẢI
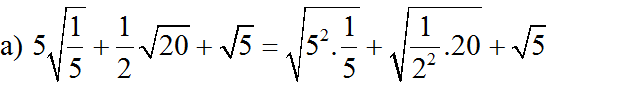
= √5 + √5 + √5 = 3√5

c) √20 - √45 + 3√18 + √72 = √4.5 - √9.5 + 3√9.2 + √36.2 = 2√5 - 3√5 + 9√2 + 6√2
= -√5 + 15√2
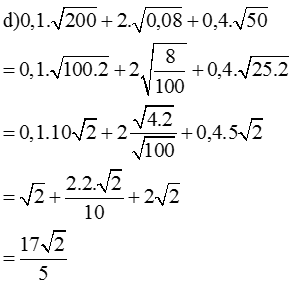
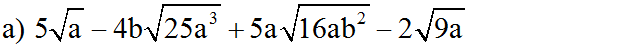
= 5√a - 4b.5a√a + 5a.4b√a - 2.3√a = 5√a - 20ab√a + 20ab√a - 6√a = -√a
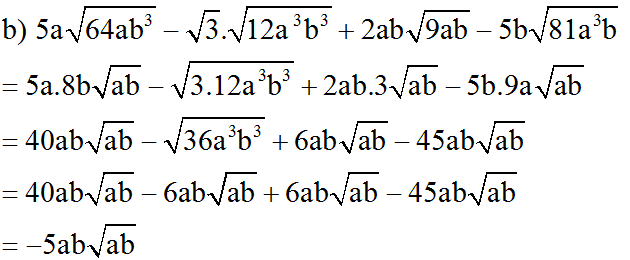
a) Rút gọn:
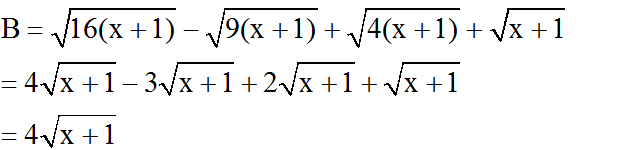
b) Để B = 16 thì:
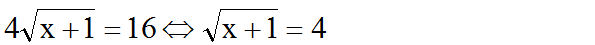
⇔ x + 1 = 16 ⇔ x = 15 (thỏa mãn x ≥ -1)
a) Biến đổi vế trái:
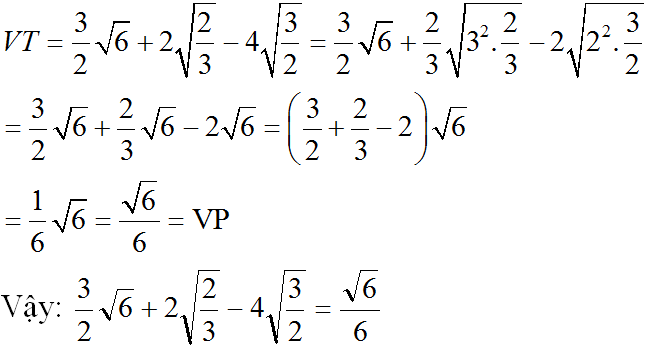
b) Biến đổi vế trái:
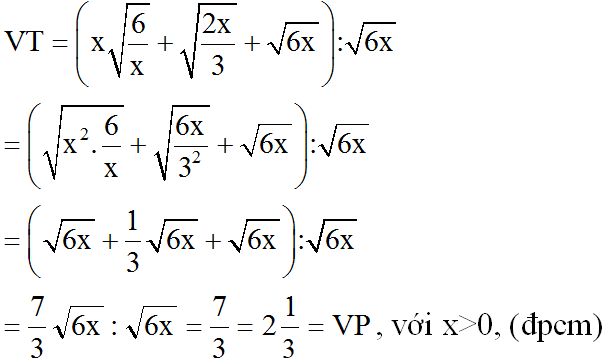
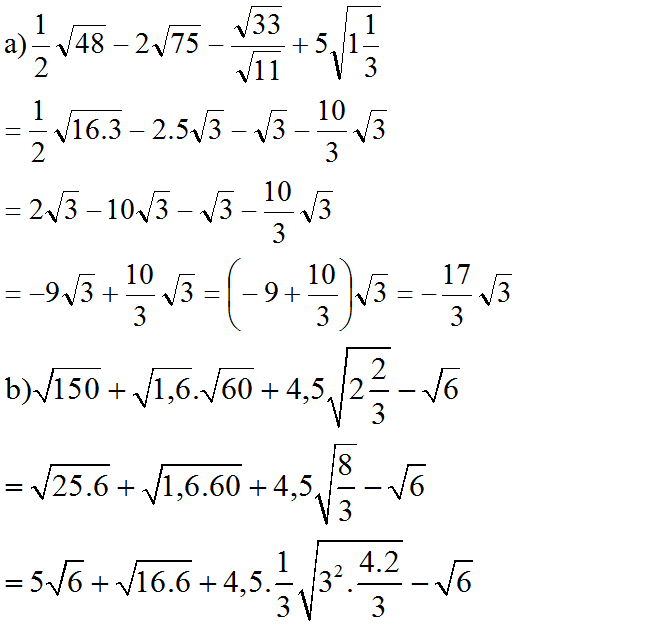
= 9√6 + 3√6 - √6 = 11√6
c) (√28 - 2√3 + √7)√7 + √84 = (√4.7 - 2√3 + √7)√7 + √4.21 = (2√7 - 2√3 + √7)√7 + 2√21
= (3√7 - 2√3)√7 + 2√21 = 3.7 - 2√21 + 2√21 = 21
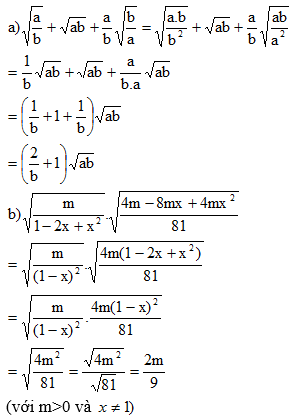
a) Biến đổi vế trái:
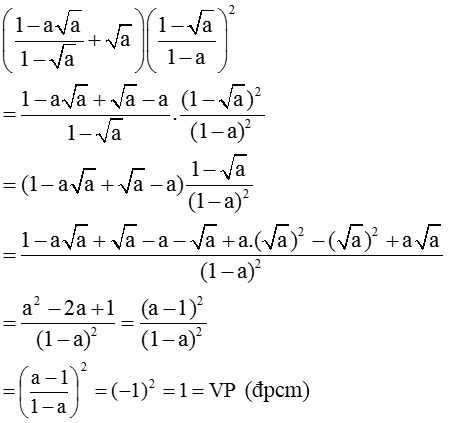
b) Biến đổi vế trái:
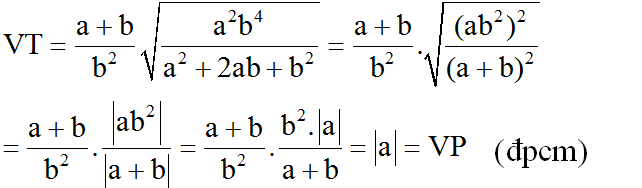
(vì a + b > 0 nên |a + b| = a + b; b2 > 0)
HƯỚNG DẪN GIẢI
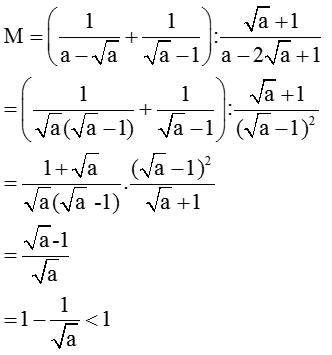
Vậy M < 1.
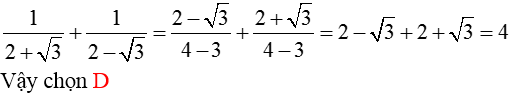
∛-729 = ∛(-9)3 = -9
∛0,064 = ∛(0,4)3 = 0,4
∛-0,216 = ∛(-0,6)3 = -0,6
∛-0,008 = ∛(-0,2)3 = -0,2
Chú ý: Bạn có thể tìm các căn bậc ba ở trên bằng máy tính bỏ túi.
(Ghi nhớ: Các bạn nên ghi nhớ một số lũy thừa bậc 3 của các số < 10:
23 = 8; 33 = 27; 43 = 64; 53 = 125;
63 = 216; 73 = 343; 83 = 512; 93 = 729)
a) ∛27 - ∛-8 - ∛125 = ∛33 - ∛(-2)3 - ∛53 = 3 - (-2) - 5 = 3 + 2 - 5 = 0
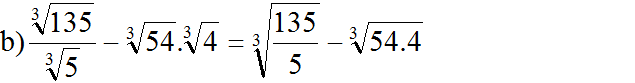
= ∛27 - ∛216 = ∛33 - ∛63 = 3 - 6 = -3
a) Ta có: 5 = ∛53 = ∛125. Vì ∛125 > ∛123 nên 5 > ∛123
b) Ta có: 5∛6 = ∛53.6 = ∛125.6 = ∛750
6∛5 = ∛63.5 = ∛216.5 = ∛1080
Vì ∛750 < ∛1080 nên 5∛6 < 6∛5
HƯỚNG DẪN GIẢI


a)(√8 - 3√2 + √10)√2 - √5 = (√22.2 - 3√2 + √5.2)√2 - √5 = (2√2 - 3√2 + √5.√2)√2 - √5
= (2 - 3 + √5)√2.√2 - √5 = (-1 + √5).2 - √5 = -2 + 2√5 - √5 = -2 + √5
b) 0,2√((-10)2.3) + 2√(√3 - √52) = 0,2.10√3 + 2|√3 - √5| = 2√3 + 2(√5 - √3)
= 0,2.10.√3 + 2|√3 - √5| = 2√3 + 2(√5 - √3) = 2√3 + 2√5 - 2√3 = 2√5
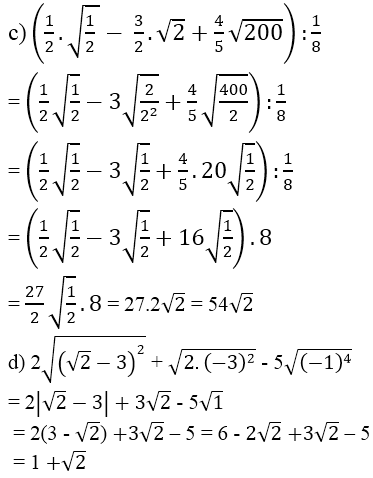
a) xy - y√x + √x - 1 = (√x)2.y - y√x + √x - 1 = y√x(√x - 1) + √x - 1 = (√x - 1)(y√x + 1) với x ≥ 1
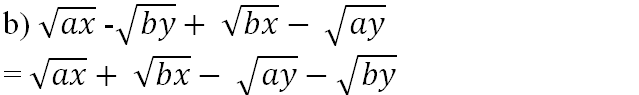
= √x(√a + √b) - √y(√a + √b) = (√a + √b)(√x - √y) (với x, y, a và b đều không âm)
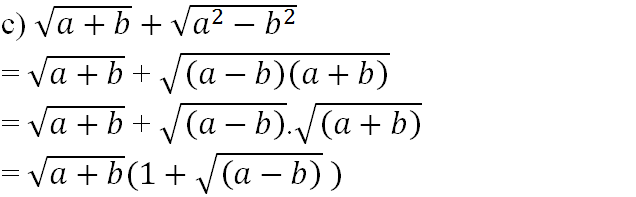
(với a + b, a - b đều không âm)
d) 12 - √x - x = 16 - x - 4 - √x (tách 12 = 16 - 4 và đổi vị trí)
= [42 - (√x)2] - (4 + √x) = (4 - √x)(4 + √x) - (4 + √x) = (4 + √x)(4 - √x - 1) = (4 + √x)(3 - √x)
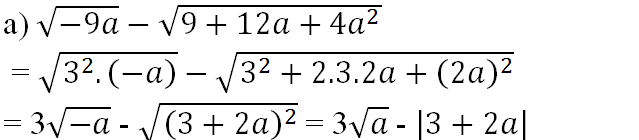
Tại a = -9 ta được:
= 3√-(-9) - |3 + 2(-9)| = 3√32 - |3 - 18| = 3.3 - |-15| = 9 - 15 = -6
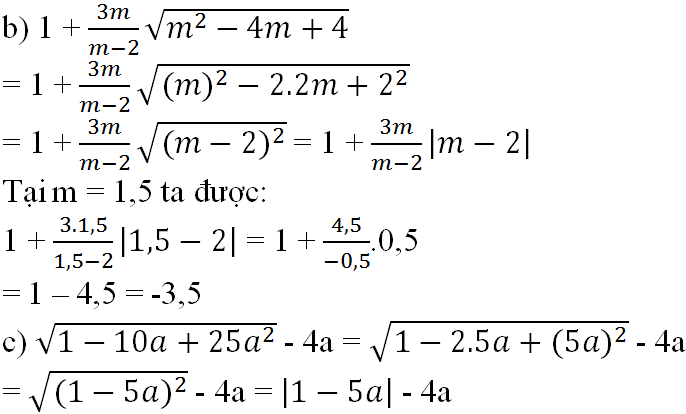
Tại a = √2 ta được:
= |1 - 5√2| - 4√2 = (5√2 - 1) - 4√2 = √2 - 1
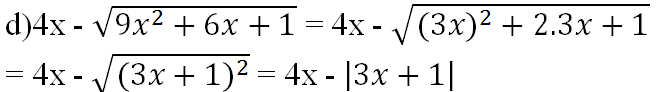
Tại x = -√3 ta được:
= 4(-√3) - |3(-√3) + 1| = -4√3 - |-3√3 + 1| = -4√3 - (3√3 - 1) = -7√3 + 1
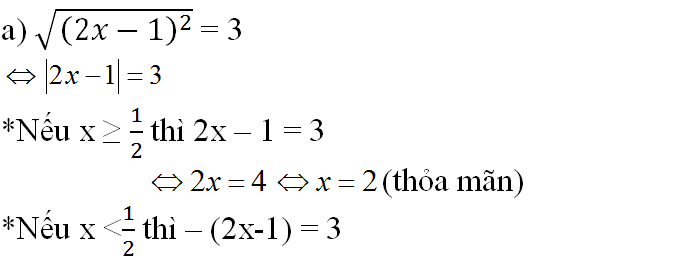
⇔ -2x + 1 = 3 ⇔ -2x = 2 ⇔ x = -1 (thỏa mãn)
Vậy phương trình có 2 nghiệm: x = 2 và x = -1
= (1 + √a)(1 - √a) = 1 - (√a)2 = 1 - a = VP (đpcm)
a) Rút gọn
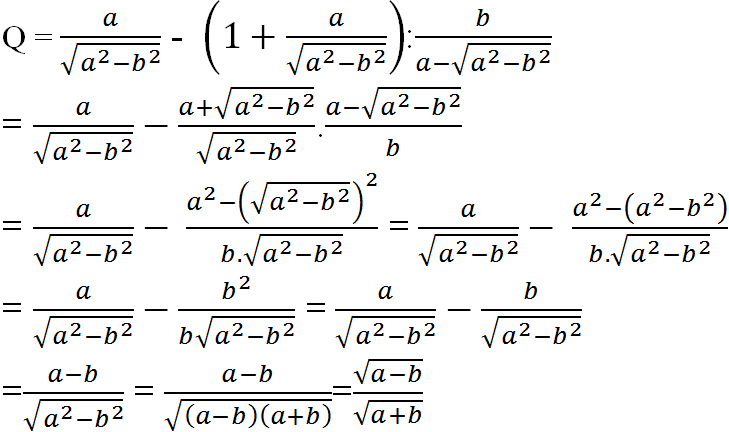
b) Thay a = 3b vào ta được:
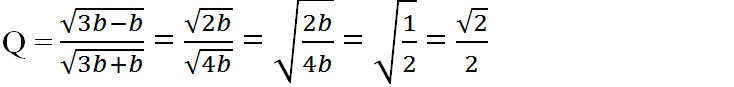












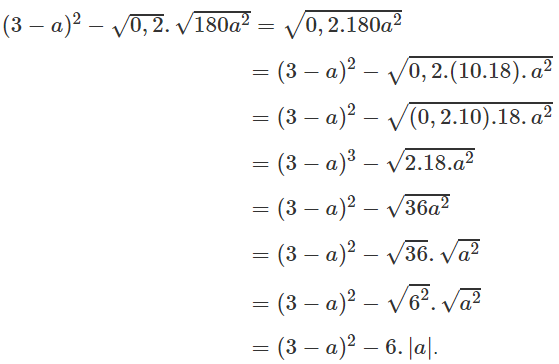
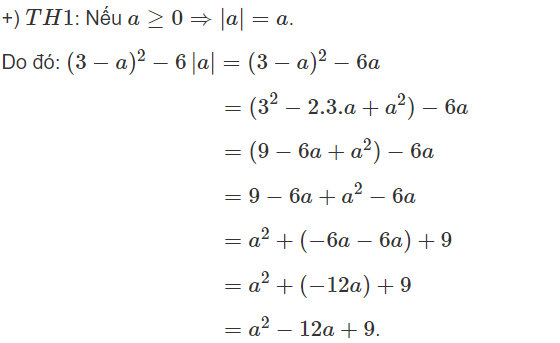
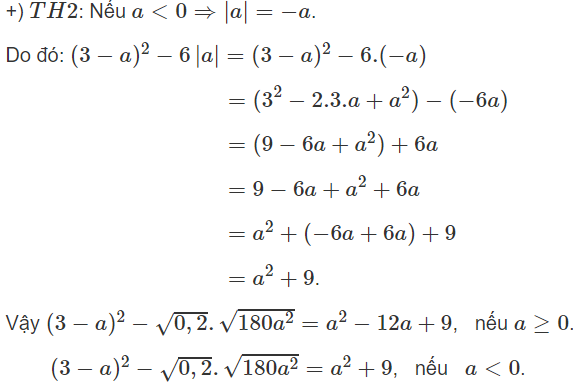







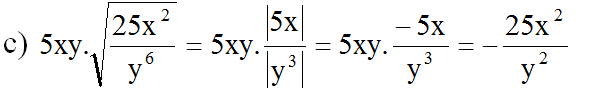
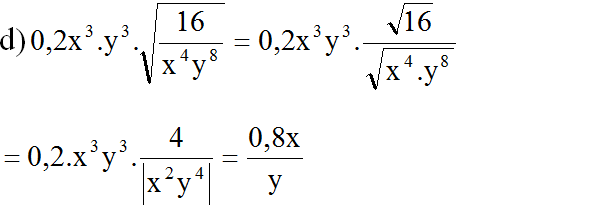

























Nhận xét
Đăng nhận xét