[HH11] HHKG - &01. Quan hệ song song trong không gian

 

Hướng dẫn giải.

Bài 1. Mệnh đề a) sai vì có vô số mặt phẳng đi qua 3 điểm thẳng hàng cho trước .

Mệnh đề b), c) Đúng.

Bài 2. Thường 4 chân của vật nằm trên 1 mặt phẳng , vật không cập kênh (gập ghềnh) nhưng mặt đất thường không phẳng, do đó bàn hoặc ghế thường hay cập kênh.

Bài 3. Đặt thước trên bàn, đẩy thước di động. Nếu mặt bàn phẳng thì cạnh thước lúc nào cũng sát với mặt bàn, nếu mặt bàn không thật phẳng thì cạnh thước có lúc không sát với mặt bàn và ta trông thấy có khe hở giữa cạnh thước và mặt bàn

Căn cứ vào định lí : “Nếu một đường thẳng đi qua hai điểm phân biệt của 1 mặt phẳng thì mọi điểm của đường thẳng đều nằm trong mặt phẳng đó”.

Bài 4. Ta có (P) ∩(Q) = Δ

Giả sử I = a ∩ b

Ta có I Є a mà a ⊂ (P) nên I Є (P)

I Є b mà b ⊂ (Q) nên I Є (Q)

Bài 5. 

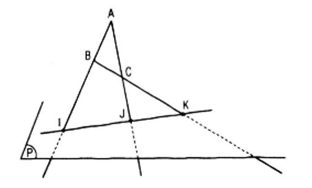
Gọi I, J, K lần lượt là giao điểm của AB, AC, BC với mp(P). A, B, C không thẳng hàng nên có mp (ABC)

Rõ ràng I, J, K Є mp(ABC) và I, J, K Є mp(P) nên I, J, k nằm trên giao tuyến của hai mp(P) và (ABC).

Vậy I, J, K thẳng hàng.

Bài 6. a), b) mệnh đề sai vì có vô số mặt phẳng đi qua 1 điểm và một đường thẳng chứa điểm đó. Mệnh đề c) đúng

Bài 7. Mệnh đề a ) sai vì có vô số mặt phẳng đi qua hai đường thẳng trùng nhau.

Mệnh đề c) sai vì không có mặt phẳng nào đi qua 2 đường thẳng chéo nhau.

Mệnh đề b) đúng.

Bài 8. Không. Bởi vì nếu a và b cắt nhau tại I thì đường thẳng c qua I cắt cả a và b nhưng nó có thể không thuộc mp(a, b)

Bài 9.

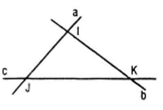
Gọi I = a ∩ b; J = a ∩ c , K = b ∩ c. Nếu các điểm I, J, k phân biệt từng cặp thì a, b, c cùng thuộc mặt phẳng (IJK), trái giả thiết. Vậy I, J, K trùng nhau do đó a, b, c đồng quy

Bài 10.

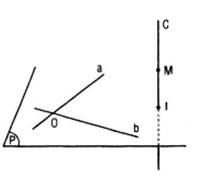
Ta có M Є (M, a) ∩ (M, b)

Vì O = a ∩ b nên O Є (M, a) ∩ (M, b) ⇔ (M, a) ∩ (M, b) = MO

Vì M Є c nên MO ⊂ mp(O, c)

Vậy giao tuyến của hai mặt phẳng (M, a), (M, b) nằm trên mp(O, c) cố định

Bài 11.

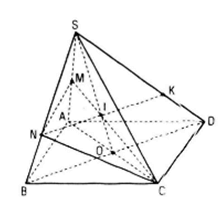
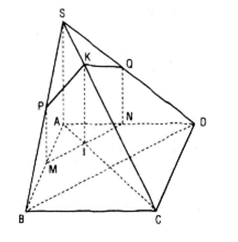
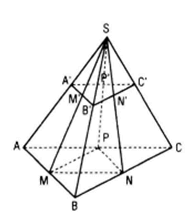
a) Tìm SO ∩ (CMN)

Trong mặt phẳng (SAC) gọi I là giao điểm của so với CM :

I = SO ∩ CM

Mà CM ⊂ (CMN) nên I = SO ∩ (CMN)

b) Tìm (SAD) ∩(CMN)

Trong mp(SBD) gọi K là giao điểm của NI và SD. K = NI ∩ SD

Ta có M, K Є (CMN) và M, K Є (SAD)

Do đó (SAD) ∩ (CMN)= MK

Bài 12.

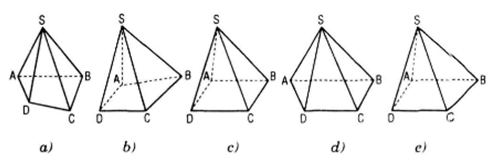
- Nếu đáy của hình chóp là tứ giác lồi tùy ý, ta có hình thường dùng là hình a) hoặc hình b).

- Nếu đáy của hình chóp tứ giác là hình bình hành , hình chữ nhật, hình thoi hay hình vuông, ta có hình biểu diễn thường dùng của hình chóp là hình c).

- Nếu đáy của hình chóp từ giác là hình thang ABCD (AB//CD) thì ta có hình biễu diễn thường dùng là hình d) hoặc hình e).

Bài 13. Thiết diện của một hình tứ diện là một tam giác khi mặt phẳng cắt ba mặt của tứ diện. Thiết diện là một tứ giác khi mặt phẳng cắt bốn mặt của hình tứ diện. Thiết diện của một hình tứ diện không thể là một ngũ giác vì ngũ giác có năm cạnh mà tứ diện có bốn mặt.

Bài 14. Cắt theo mẫu sau:

Bài 15. Gọi O = AC ∩ BD ; O’ = A’C’ ∩ SO ; D’ = B’O’ ∩ SB

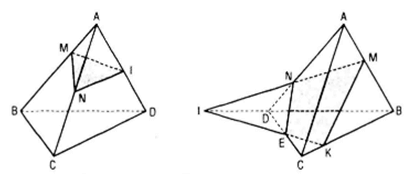
- Nếu D thuộc đoạn thẳng SD thì thiết diện là tứ giác A’B’C’D’

- Nếu D’ nằm trên phần kéo dài của cạnh SD , ta gọi E là giao điểm của CD và C’D’ , F là giao điểm của AD và A’D’.

Khi ấy thiết diện là ngũ giác A’B’C’EF

Bài 16.

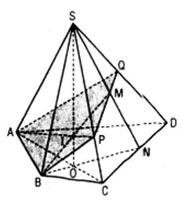
a) Tìm (SBM) ∩ (SAC)

Trong đó ΔSAD gọi N = SM ∩ CD

Trong mp(ABCD) gọi O = BN ∩ AC

Ta có : SO = (SBM) ∩ (SAC)

b) Tìm BM ∩ (SAC)

- Chọn mặt phẳng phụ chưa BM là (SBN)

- (SBN) ∩ (SAC) = SO

- Gọi I = SO ∩ BM thì I = BM ∩ (SAC)

c) Trong mp(SAC) gọi P = AI ∩ SC

Trong mp(SCD) PM cắt tại Q . Thiết diện của hình chóp khi cắt bởi mp(ABM) là tứ giác ABPQ

Bài 17.

a) Mệnh đề đúng

b) Mệnh đề sai(xét trường hợp hai đường thẳng song song)

c) Mệnh đề sai(xét hai đường thẳng cắt nhau)

d) Mệnh đề đúng

Bài 18.

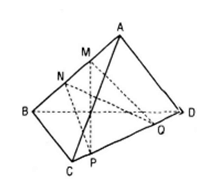
Hai đường thẳng MQ và NP chéo nhau. Thật vậy giả sử chúng không chéo nhau, tức chúng cùng thuộc một mp(α) nào đó. Vậy M, N, P, Q cùng thuộc mp(α) và do đó A, B, C, D cùng thuộc mp(α). Điều này mâu thuẫn với giả thiết ABCD là một tứ diện.

Chứng minh tương tự, hai đường thẳng MP và NQ cũng chéo nhau

Bài 19.

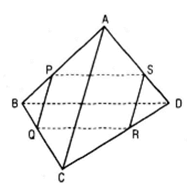
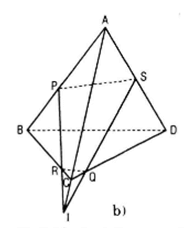
a) Nếu P, Q, R, S, đồng phẳng thì chúng cùng thuộc mp(PQRS)

Ta có : (PQRS) ∩ (ABC) = PQ ; (PQRS) ∩(ACD) = RS ; (ABC) ∩ (ACD) = AC

Theo định lí về giao tuyến của ba mặt phẳng thì PQ, SR, AC hoặc đôi một song song hoặc đồng quy.

Ngược lại, nếu ba đường thẳng PQ, SR, AC hoặc đôi một song song hoặc đồng quy thì hai đường thẳng PQ và RS hoặc song song hoặc cắt nhau. Vậy hai đường thẳng PQ và RS cùng thuộc một mặt phẳng, từ 4 điểm P, Q, R, S đồng phẳng.

b) Chứng minh tương tự câu a)

Bài 20.

a) Trường hợp PR// AC

hai mp(PQR) và (ACD) có điểm chung Q và lần lượt chứa hai đường thẳng song song PR và AC nên: (PQR) ∩ (ACD) = Qt // AC

Gọi {S} = Qt // AC thì {S} = AD ∩ (PQR)

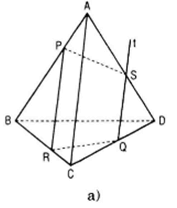
b) Trường hợp PR cắt AC

Giải sử {I} = PR ∩ AC ⇔ (PQR) ∩(ACD) = QI

Trong mp(ACD) ta có : {S} = QI ∩ AD thì {S} = AD ∩ (PQR)

Bài 21.

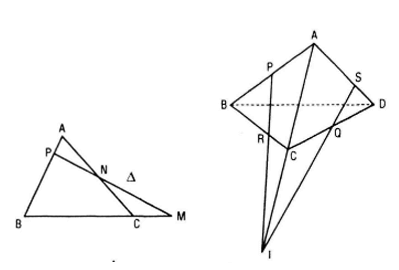
Định lí Menelaus

Giải sử đường thằng Δ cắt các cạnh (hoặc phần kéo dài) BC, CA, AB lần lượt tại M, N, P thì :

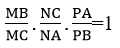
ÁP dụng định lí để giải bài toán

Gọi {I}= PR ∩ AC

Trong mp(ACD) gọi {S} = QI ∩ AD thì {S} = AD ∩ (PQR)

Áp dụng định lí Menelaus trong ΔABC với cắt tiếp tuyến PRI ta có :

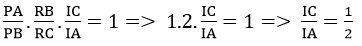
⇒ C là trung điểm của AI

Áp dụng định lí Menelaus trong ΔACD với cát tuyến IQS ta có :

Bài 22.

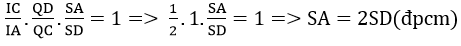
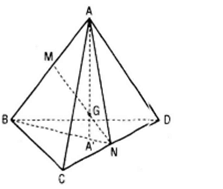
a) Trong mp(ABN) gọi A’ là giao điểm của AG với trung tuyến BN của ΔBCD . Ta chứng minh:

A’B = 2A’N

Áp dụng định lí Menelaus trong ΔBMN với cát tuyến AGA’ Ta có :

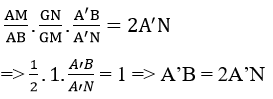
Vậy A’ là trọng tâm của Δ BCD

Tương tự BG, CG, DG lần lượt đi qua trọng tâm B’, C’, D’ của tam giác ACD, ABD, ABC

b) Chứng minh GA = 3GA’

Áp dụng định lí Menelaus trong ΔABA’ với cát tuyến MGN Ta có :

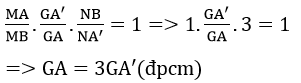
Hướng dẫn giải.

Bài 23. Mệnh đề c) và e) đúng

Bài 24. Mệnh đề a) sai vì có thể b ⊂ (P)

Mệnh đề b) đúng

Mệnh đềc) sai vì có thể b // (P)

Mệnh đề d) đúng

Mệnh đề e) sai vì b cắt (P)

Mệnh đề f) đúng

Bài 25.

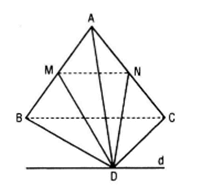
a) MN là đường trung bình của tam giác ABC nên MN //BC ⇔ MN // mp(BCD) (vì MN ⊄ (BCD))

b) Vì MN // mp(BCD) nên mp(DMN) đi qua MN cắt mp(BCD) theo giao tuyến d // MN cắt mp(BCD) theo giả thiết d // MN do đó d // mp(ABC).

Bài 26.

a) Có thể cắt tứ diện bằng một mặt phẳng để thiết diện là hình thang, ví dụ như mặt phẳng đi qua M, N (M, N là hai điểm lần lượt nằm trên hai cạnh AB, BC) và song song với BD

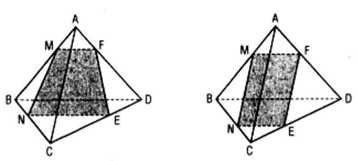
b) Có thể cắt tứ diện bằng một măt phẳng để thiết diện là hình bình hành, ví dụ như mặt phẳng đi qua điểm M nằm trên cạnh AB và song song với hai đường thẳng BD và AC .

c) Có thể. Giả sử mặt phẳng cắt là (P) qua điểm M thuộc đoạn AB , song song với BD và AC . Khi đó thiết diện là hình bình hành MNEF

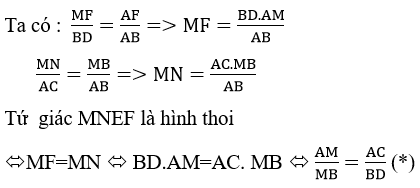
Vậy với M xác định ở (*) thì mp(P) qua M và song song với AC , BD sẽ cắt tứ diện theo một thiết diện là hình thoi

Bài 27.

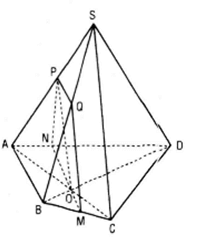
Gọi (α) là mặt phẳng qua O song song với AB và SC.

AB // (α) nên (α ) cắt mp(ABCD) theo giao tuyến qua O và song song với AB . Gọi M, N lần lượt là giao điểm của đường thẳng qua O song song AB với BC và AD.

Trong mp(SAC) kẻ OP // SC (P Є AS) (α) cắt mp(SAB) theo giao tuyến PQ // AB (Q Є SB)

Thiết diện cần tìm là tứ giác MNPQ.

Bài 28.

Gọi (β) LÀ mặt phẳng qua M và song song với BD, SA

BD // (β) nên (β) cắt mp(ABCD) theo giao tuyến MN // BD (N Є AD)

SA//(β) nên (β) cắt mp(SAB) theo giao tuyến MP // SA (P Є SB)

(β) cắt mặt phẳng (SAD) theo giao tuyến NQ//SA(Q Є SD)

Gọi I = MN ∩ AC . (β) cắt mp(SAC) theo giao tuyến IK // SA (K Є SC)

Thiết diện cần tìm là ngũ giác MNQKP.

Bài 29.

a) Sai vì hai mặt phẳng có thể cắt nhau theo giao tuyến song song với đường thẳng đã cho

b) Đúng

c) Đúng

d) Sai

e) Sai vì có thể hai mặt phẳng cắt nhau

f) Đúng

Bài 30.

a) Đúng.

b) Sai vì cạnh đáy không song song với cạnh bên.

c) Sai.

d) Đúng.

e) Đúng.

Bài 31.

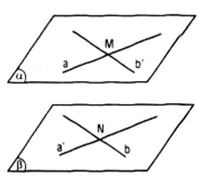
Gọi hai đường thẳng chéo nhau là a và b.

- Trên đường thẩng a ta lấy điểm M, qua M kẻ đường thẳng b’ // b.

- Trên đường thẳng b ta lấy điểm N, qua N ta kẻ đường thẳng a’ // a.

- Gọi (α) = mp(a, b’), (β) = mp(b, a’) thì (α) // (β) .

- Ta chứng tỏ cặp mp(α) , (β) là duy nhất . Thật vâỵ giả sử tồn tại cặp (α’) , (β’) sao cho (α’) chứa a, (β’) chứa b và (α’) // (β’). Ta chứng minh (α’) ≡ (α) và (β’) ≡ (β)

+ Do (α’) và (α) cùng chứa a, nên nếu (α’) và (α) không trùng nhau thì (α’) ∩ (α)= a (1)

+ Do (α’) // (β’) ⇒ b // (α) (2)

+ Do (α) // (β) ⇒ b // (α) (3)

Từ (1) , (2), (3) suy ra a // b mâu thuẫn giả thiết

Vậy (α’) ≡(α), tương tự (β’) ≡ (β)

Do đó cặp mp(α), (β) duy nhất.

Bài 32.

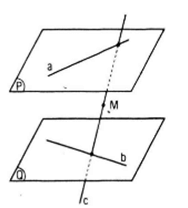
Giả sử c = mp(M, a) ∩ mp(M, b). Ta cần chứng minh c cắt cả a và b. Vì c và a cùng nằm trên một mặt phẳng và không thể trùng nhau (do c qua M và a không đi qua M) nên hoặc c // a hoặc c cắt b. Cũng vậy hoặc c // b hoặc c cắt b. Không thể xảy ra đồng thời c // a, c // b vì a, b chéo nhau. Vậy nếu c song song với a thì c phải cắt b , tức là c qua một điểm của mp(Q), và do đó M thuộc (Q) (trái giả thiết). Tương tự, không thể có c song song với b. Tóm lại c phải cắt a và b

Nếu còn có đường thẳng c’ khác đi qua M, cắt cả a và b thì a và b đồng phẳng. Vô lí

Bài 33.

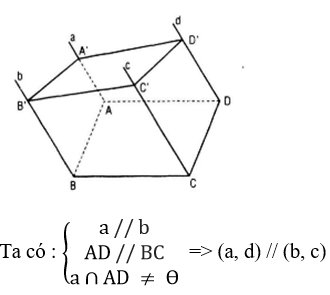
Tương tự (a, b) // (c, d)

Vì hai mp(a, b) và (c, d) song song nhau nên mp(A’B’C’) cắt hai mặt phẳng này lần lượt theo hai giao tuyến A’B’ và C’D’ song song nhau

Tương tự A’D’//B’C’

Vậy A’B’C’D’là hình bình hành

Bài 34.

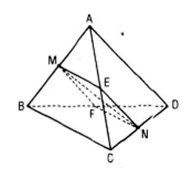
Giả sử (P) cắt BD , AC và CD lần lượt tại F, E, N

Vì AD// (P) nên (P) cắt mp(ABD) theo giao tuyến MF//AD.

Vì M là trung điểm của AB nên F là trung điểm của BD. Vì BC // (P) nên(P) cắt mp(BCD) theo giao tuyến FN // BC. Vì F là trung điểm của BD nên N là trung điểm của CD.

Bài 35.

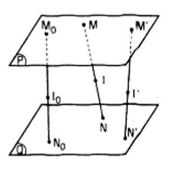
Thuận. Giả sử M Є (P) (N) Є (Q) và điểm I thuộc đoạn thẳng MN sao cho :

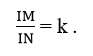
Trên hai mp(P), (Q) ta lần lượt lấy hai điểm cố định Mo và No rồi lấy một điểm Io thuộc đoạn thẳng MoNo sao cho∶

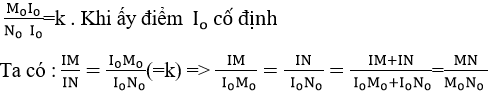
Áp dụng định lí Ta-lét đảo, ta suy ra đường thẳng IoI thuộc một mặt phẳng song song với (P) và (Q). Mp(R) cố định vì nó qua điểm cố định Io và song song với mặt phẳng cố định (P). Vậy điểm I thuộc mp(R) cố định

Đảo. Ngược lại, lấy một điểm I’ bất kì trên mp(R). Qua I’ ta kẻ một đường thẳng cắt hai mp(P) và (Q) lần lượt tại M’, N’. Xét hai cát tuyến MoNo, M’N’ và ba mặt phẳng song song (P), (Q), (R) . Theo định lí ta-lét ta có :

Bài 36.

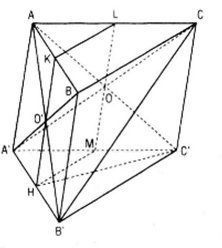
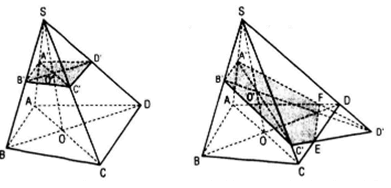
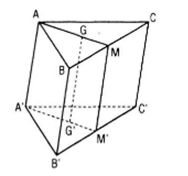
a) Chứng minh CB’// (AHC’) ta tìm trong(AHC’) một đường thẳng song song với CB’ , muốn vậy ta tìm giao điểm của một mặt phẳn chứA CB’ với (AHC’) đó là (A’C’B’). Gọi O là giao điểm AC và A’C.AA’C’C là hình bình hành nên O là trung điểm của A’C

Do đó HO là đường trung bình của ΔA’B’C’ ⇔ HO // BC ⇒ BC // (AHC’)

(Vì HO ⊂ (AHC’) )

b) Tìm giao tuyến d của (A’B’C’) và (A’BC)

Gọi O là giao điểm của AB’ và A’B thì O, O’ là hai điểm chung của hai mặt phẳng

(AB’C’) và (A’BC) nên : (AB’C’) ∩ (A’BC) = OO’

Vậy d = OO’. Ta có O’ là trung điểm của AB’(vì AA’B’B là hình bình hành)

⇔ OO’ là đường trung bình của ΔAB’C’ ⇔ OO’ // B’C’// BC ⇒ OO’// (BB’C’C)⇒ d // (BB’C’C)

c) Gọi {K} = HO’ ∩ AB thì HK // AA’

Qua O kẻ ML// AA’(M Є A’C’, L Є AC). Thiết diện cần tìm là hình bình hành HKLM

Bài 37.

a) Chứng minh (BDA’) // (B’D’C’)

Ta có tứ giác BB’D’D và A’B’CD là các hình bình hành nên:

BD // B’D’và DA’// B’C ⇒ hai mp(BDA’) và (B’D’C’) có các cặp đường thẳng cắt nhau và song song nhau từng đôi một nên chúng song song

Vậy (BDA’)// (B’D’C’)

Chứng minh G1,G2 Є AC’

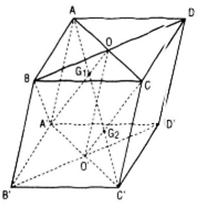
Gọi O, O’ lần lượt là tâm của hình bình hành ABCD và A’B’C’D’

Trong mp(AA’C’C) gọi G1,G2 lần lượt là giao điểm của AC’với A’O và O’C. Ta chứng minh G1,G2, lần lượt là trọng tâm của ΔA’BD và ΔCB’D’

Thật vây, ta có ΔG1OA ∼ ΔG1A'C'(vì AC // A’C’)

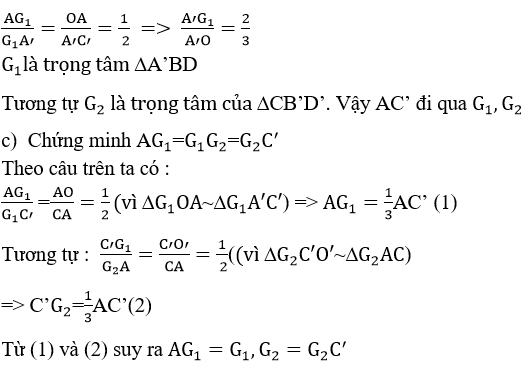
d) Gọi M, N, P, Q, S, R lần lượt là trung điểm của các cạnh :

AB, AD, DD’, C’D’, C’B’, BB’

Bài 38.

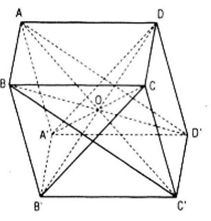
Áp dụng tính chất “Trong một hình bình hành tổng bình phương hai đường chéo bằng tổng bình phương bốn cạnh”.

Đặt : AB = a, BC = b, AA’= c (đó là 3 kích thước của hình hộp)

Trong hình bình hành ABC’D’ Ta có : AC2 + BD2 = 2(a2 + BC2 )(1)

Tron hình bình hành A’B’CD Ta có : A'C2 + BD2 = 2(a2 + B'C2 )(2)

Cộng (1) và (2) ta được : AC2 + BD2 + A'C2 + B'D2 = 2(2a2 + BC'2 + B'C2 (3)

Mặt khác trong hình bình hành BB’C’C Ta có BC2 + B'C2 = 2(b2 + c2 )(4)

Thay (4) và (3) ta được : AC2 + BD2 + A'C2 + B'D2 = 4(a2 + b2 + c2)(đpcm)

Bài 39.

Gọi S là giao điểmcác cạnh AA’, BB’, CC’ của hình chóp cụt do A’B’//AB và M’, M lần lượt là trung điểm của A’B’, AB nên MM’ đi qua S . Tương tự NN’ PP’ cùng đi qua S.

Vậy MM’, NN’, PP’ đồng quy tại S.

Ta có (M’N’P’) // (MNP) nên MNP. M’N’P’ là hình chọp cụt

Hướng dẫn giải.

Bài 40.

a) Sai vì nếu hình chiếu song song của hai đường thẳng mà trùng nhau thì hai đường thẳng đó cùng thuộc 1 mặt phẳng

b) Sai vì hình chiếu song song của hai đường thẳng chéo nhau có thể song song với nhau.

c) Đúng

d) Sai

Bài 41.

a) Sai

b) Đúng

c) Đúng

d) Đúng

e) Sai

f) Đúng

Bài 42.

Gọi G là trọng tâm ΔABC, M là trung điểm BC. G’. M’ là hình chiếu song song của G, M

Ta có M’ là trung điểm B’C’ và (A'G')/(G'Ms' ) = AG/GM = 2

G là trọng tâm ΔA’B’C’

Bài 43.

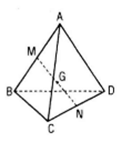
Hình biểu diễn của một tứ diện là tứ giác ABCD lấy M và N lần lượt là trung điểm AB và CD thì trung điểm G của MN sẽ biễu diễn cho trọng tâm của tứ diện.

Bài 44.

Vẽ elip tâm O là hình biễu diễn của đường tròn đã cho. Lấy B và C là hai điểm trên elip sao cho B, O, C thẳng hàng và một điểm A thuộc elip sao cho A khác B và C. Khi đó tam giác ABC là hình biễu diễn của một tam giác vuông nội tiếp trong một đường tròn.

Bài 45.

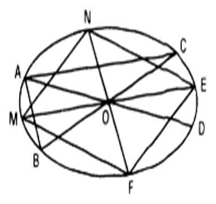
Theo bài 44 , vẽ tam giác ABC là hình biểu diễn của 1tam giác vuông nội tiếp trong 1 đường tròn . Qua O ta kẻ hai dây ME và NF của elip lần lượt song song với AC và AB . Khi đó tứ giác MNEF là hình biễu diễn của 1 hình vuông nội tiếp trong 1 đường tròn.

Bài 46.

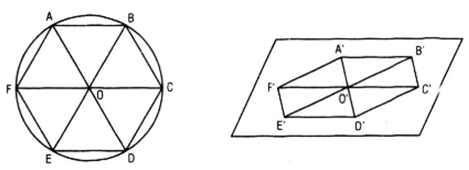
Xét hình lục giác đều ABCDEF, ta nhận thấy :

- Tứ giác OABC là hình thoi.

- Các điểm D, E, F lần lượt là các điểm đối xứng của các điểm A, B, C, qua tâm O.

Từ đó suy ra cách vẽ hình biễu diễn của lục giác đều ABCDEF như sau :

- Vẽ hình bình hành O’A’B’C’ biễu diễn cho hình thoi OABC.

- Lấy các điểm D’, E’, F’ lần lượt đối xứng với các điểm A’, B’, C’ qua O, ta được hình biễu diễn A’B’C’D’E’F’ của hình lục giác đều ABCDEF.

Bài 47.

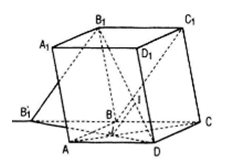
- Dựng B'1 là hình chiếu B1 qua phép chiếu song song ở trên (BC1B1B’1 là hình bình hành).

- Dựng J là giao điểm của B'1D với AC .

- Trong mp(B1B'1D) kẻ JI song song với B1B'1 cắt B1D tại I

Rõ ràng I và J thỏa mãn điều kiện của bài toán

Hướng dẫn giải.

Bài 1. 

a) Đúng

b) Sai. Có thể a // b

c) Đúng

d) Sai. Có thể a cắt b

Bài 2.

a) Sai. Có thể a cắt b hoặc a chéo b

b) Sai có thể (α) và (β) cắt nhau

c) Đúng

d) Đúng

e) Sai. có thể cắt đường thứ nhất nhưng chéo nhau với đường thứ hai

f) Đúng

g) Đúng

Bài 3. Các hình a, b, d, f, g, h

Bài 4.

Bài 5.

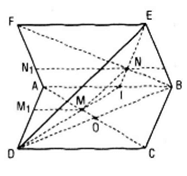
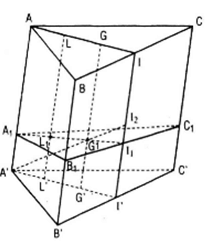
a) Gọi I , I’ lần lượt là trung điểm của các cạnh BC, B’C’ thì rõ ràng II’ song song và bằng AA’ nên tứ giác AII’A’ là hình bình hành, do đó AI song song và bằng A’I’.

c) Xét hình bình hành AII’A’. Gọi L, L’ lần lượt là trung điểm của đường thẳng AG và A’G’, L1 là giao điểm của LL’ và A1I1. Khi đó L1 là trung điểm của A1G1.

Theo định lí về đường trung bình của hình thang, ta có :

Bài 6.

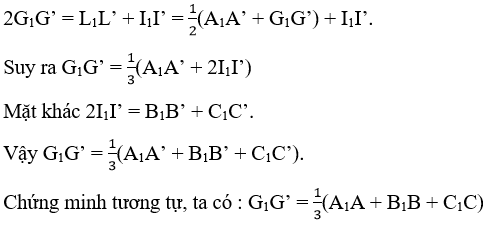
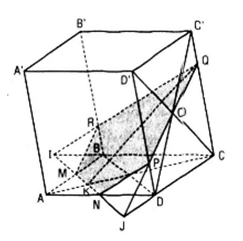
Gọi I và J lần lượt là các giao điểm của đường thẳng MN với BC và CD. Gọi P, Q lần lượt là các giao điểm của đường thẳng JO với các cạnh DD’, CC’. Gọi R là giao của BB’ và đường thẳng IQ. Ta có :

(MNO) ∩ (ABCD) = MN

(MNO) ∩ (CDD’C’) = PQ

(MNO) ∩ (ADD’A’) = NP

(MNO) ∩ (BCC’B’) = RQ

(MNO) ∩ (ABB’A’) = MR

Vậy thiết diện cần tìm là ngũ giác MNPQR

Bài 7.

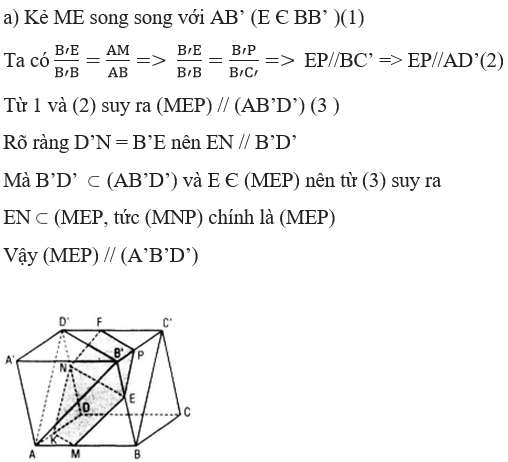
b) Từ M kẻ ME song song với AB’, từ P kẻ PF song song với B’D’ . Từ N kẻ NK song song với AD’ cắt AD tại K. Thiết diện là lục giác MEPFNK có các cạnh đối song song.

Bài 8.

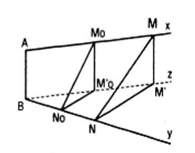
b) Thuận. Gọi O là một điểm thuộc đọa AB sao cho OA : OB = k , từ O ta vẽ hai tia Ox’ và Oy’ sao cho Ox’//Ax, Oy’//By. Xét phép chiếu song song theo phương AB lên mp(Ox’, Oy’). Gọi M’, N’ lần lượt là hình chiếu của M và N theo phép chiếu này . Khi đó giao điểmcủa MN và M’N’ chính là điểm I vì rõ ràng ta có :

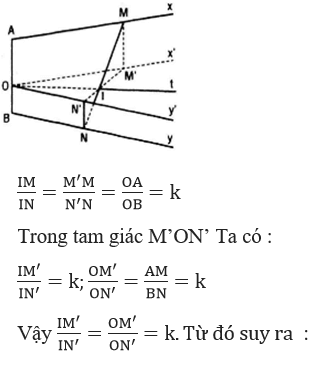
I phải nằm trên tia phân giác Ot của góc x’Oy’.

Đảo. Giả sử I là một điểm bất kì thuộc tia phân giác Ot của góc x’Oy’. Gọi M’, N’ là những điểm lần lượt thuộc tia Ox’, tia Oy’ sao cho M’, I , N’ thẳng hàng và (IM^')/(IN^' )=k (có thể tìm M’, N’ bằng cách dùng phép vị tự tâm I tỉ số -k trên mp(Ox’y’)). Gọi M, N lần lượt là những điểm thuộc các tia Ax, By sao cho AM = OM’, BN = ON’. Dễ thấy I, M, N thẳng hàng và IM : IN = k

Kết luận : Tập hợp các điểm I thỏa mãn điều kiện bài toán là tia phân giác Ot của góc x’Oy’.