[ĐS8] ĐA THỨC - &01. Nhân và chia đa thức; Hằng đẳng thức.
Hướng dẫn giải.
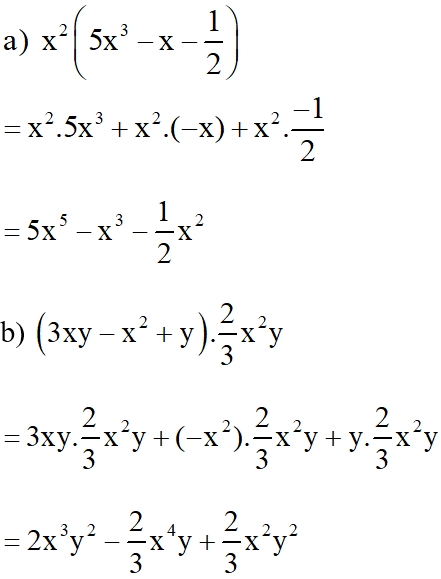
a) x(x – y) + y(x + y) = x.x – x.y + y.x + y.y = x2 – xy + xy + y2 = x2 + y2.
Tại x = –6 ; y = 8, giá trị biểu thức bằng : (–6)2 + 82 = 36 + 64 = 100.
b) x.(x2 – y) – x2.(x + y) + y.(x2 – x) = x.x2 – x.y – (x2.x + x2.y) + y.x2 – y.x
= x3 – xy – x3 – x2y + x2y – xy = (x3 – x3) + (x2y – x2y) – xy – xy = –2xy
Tại 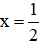
a) 3x(12x – 4) – 9x(4x – 3) = 30
3x.12x – 3x.4 – (9x.4x – 9x.3) = 30
36x2 – 12x – 36x2 + 27x = 30
(36x2 – 36x2) + (27x – 12x) = 30
15x = 30
x = 2
Vậy x = 2.
b) x(5 – 2x) + 2x(x – 1) = 15
(x.5 – x.2x) + (2x.x – 2x.1) = 15
5x – 2x2 + 2x2 – 2x = 15
(2x2 – 2x2) + (5x – 2x) = 15
3x = 15
x = 5.
Vậy x = 5.
+ Cộng thêm 5 ⇒ x + 5
+ Được bao nhiêu đem nhân với 2 ⇒ (x + 5).2
+ Lấy kết quả trên cộng với 10 ⇒ (x + 5).2 + 10
+ Nhân kết quả vừa tìm được với 5 ⇒ [(x + 5).2 + 10].5
+ Đọc kết quả cuối cùng sau khi đã trừ đi 100 ⇒ [(x + 5).2 + 10].5 – 100
Rút gọn biểu thức trên :
[(x + 5).2 + 10].5 – 100 = (x.2 + 5.2 + 10).5 – 100 = (2x + 20).5 – 100
= 2x.5 + 20.5 – 100 = 10x + 100 – 100 = 10x
Vậy kết quả cuối cùng bằng mười lần số tuổi thực của bạn. Do đó ta chỉ cần lấy kết quả cuối cùng chia cho 10 là ra số tuổi thực.
a) x(x – y) + y(x – y) = x.x – x.y + y.x – y.y = x2 – xy + xy – y2 = x2 – y2 + (xy – xy) = x2 – y2
b) xn - 1(x + y) - y(xn - 1+ yn - 1 =xn - 1.x + xn - 1.y - y.xn - 1- y.yn - 1 =xn+ xn - 1y - xn - 1y - yn =xn-yn
a(-1)(-1 – 1) + 13 (- 1 + 1) = (-a).(-2) + 1.0 = 2a
Vậy đánh dấu x vào ô tương ứng với 2a.
a) (x2 – 2x + 1)( x – 1) = x2.(x – 1) + (–2x).(x – 1) + 1.(x – 1)
= x2.x + x2.(– 1) + (– 2x).x + (–2x).(–1) + 1.x + 1.(–1) = x3 – x2 – 2x2 + 2x + x – 1
= x3 – (x2 + 2x2) + (2x + x) – 1 = x3 – 3x2 + 3x – 1
b) (x3 – 2x2 + x – 1)(5 – x) = (x3 – 2x2 + x – 1).5 + (x3 – 2x2 + x – 1).(–x)
= x3.5 + (–2x2).5 + x.5 + (–1).5 + x3.(–x) + (–2x2).(–x) + x.(–x) + (–1).(–x)
= 5x3 – 10x2 + 5x – 5 – x4 + 2x3 – x2 + x = –x4 + (5x3 + 2x3) – (10x2 + x2) + (5x + x) – 5
= –x4 + 7x3 – 11x2 + 6x – 5
Ta có: (x3 – 2x2 + x – 1).(x – 5) = (x3 – 2x2 + x – 1).[–(5 – x)]
= – (x3 – 2x2 + x – 1).(5 – x) = – (–x4 + 7x3 – 11x2 + 6x – 5) = x4 – 7x3 + 11x2 – 6x + 5.
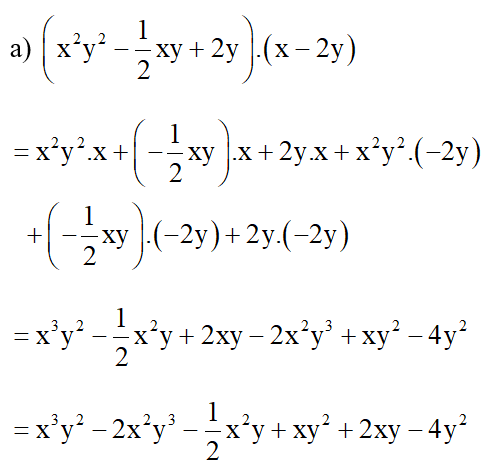
b) (x2 – xy + y2)(x + y) = (x2 – xy + y2).x + (x2 – xy + y2).y
= x2.x + (–xy).x + y2.x + x2.y + (–xy).y + y2.y = x3 – x2y + xy2 + x2y – xy2 + y3
= x3 + y3 + (xy2 – xy2) + (xy2 – xy2) = x3 + y3
A = (x – y).(x2 + xy + y2) = x.(x2 + xy + y2) + (–y).(x2 + xy + y2)
= x.x2 + x.xy + x.y2 + (–y).x2 + (–y).xy + (–y).y2 = x3 + x2y + xy2 – x2y – xy2 – y3
= x3 – y3 + (x2y – x2y) + (xy2 – xy2) = x3 – y3.
Tại x = –10, y = 2 thì A = (–10)3 – 23 = –1000 – 8 = –1008
Tại x = –1 ; y = 0 thì A = (–1)3 – 03 = –1 – 0 = –1
Tại x = 2 ; y = –1 thì A = 23 – (–1)3 = 8 – (–1) = 9
Tại x = –0,5 ; y = 1,25 thì A = (–0,5)3 – 1,253 = –0,125 – 1,953125 = –2,078125
Vậy ta có bảng sau :
| Giá trị của x và y | Giá trị biểu thức (x – y)(x2 + xy + y2) |
| x = -10 ; y = 2 | -1008 |
| x = -1 ; y = 0 | -1 |
| x = 2 ; y = -1 | 9 |
| x = -0,5 ; y = 1,25 | -2,078125 |
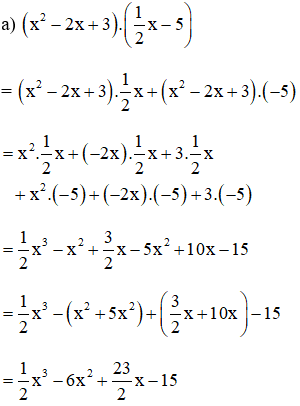
b) (x2 – 2xy + y2)(x – y) = (x2 – 2xy + y2).x + (x2 – 2xy + y2).(–y)
= x2.x + (–2xy).x + y2.x + x2.(–y) + (–2xy).(–y) + y2.(–y)
= x3 – 2x2y + xy2 – x2y + 2xy2 – y3 = x3 – (2x2y + x2y) + (xy2 + 2xy2) – y3
= x3 – 3x2y + 3xy2 – y3.
= (x.2x + x.3) + (–5).2x + (–5).3 – (2x.x + 2x.(–3)) + x + 7
= 2x2 + 3x – 10x – 15 – 2x2 + 6x + x + 7 = (2x2 – 2x2) + (3x – 10x + 6x + x) + 7 – 15 = – 8
Vậy với mọi giá trị của biến x, biểu thức luôn có giá trị bằng –8
A = (x2 – 5)(x + 3) + (x + 4)(x – x2) = x2.(x + 3) + (–5).(x + 3) + x.(x – x2) + 4.(x – x2)
= x2.x + x2.3 + (–5).x + (–5).3 + x.x + x.(–x2) + 4.x + 4.(–x2)
= x3 + 3x2 – 5x – 15 + x2 – x3 + 4x – 4x2
= (x3 – x3) + (3x2 + x2 – 4x2) + (4x – 5x) – 15 = –x – 15.
a) Nếu x = 0 thì A = –0 – 15 = –15
b) Nếu x = 15 thì A = –15 – 15 = –30
c) Nếu x = –15 thì A = –(–15) – 15 = 15 – 15 = 0
d) Nếu x = 0,15 thì A = –0,15 – 15 = –15,15
Hướng dẫn giải.
VT = (12x – 5)(4x – 1) + (3x – 7)(1 – 16x)
= 12x.(4x – 1) + (–5).(4x – 1) + 3x.(1 – 16x) + (–7).(1 – 16x)
= 12x.4x+ 12x.(–1) + (–5).4x + (–5).(–1) + 3x.1 + 3x.(–16x) + (–7).1 + (–7).(–16x)
= 48x2 – 12x – 20x + 5 + 3x – 48x2 – 7 + 112x
= (48x2 – 48x2) + (– 12x – 20x + 3x + 112x) + (5 – 7) = 83x – 2
Vậy ta có: 83x – 2 = 81
83x = 81 + 2
83x = 83
x = 83 : 83
x = 1.
Tích của hai số sau là (a + 2)(a + 4)
Tích của hai số đầu là a.(a + 2)
Theo đề bài ta có: (a + 2)(a + 4) – a(a + 2) = 192
a.(a + 4) + 2.(a + 4) – a.(a + 2) = 192
a2 + 4a + 2a + 8 – a2 – 2a = 192
(a2 – a2) + (4a + 2a – 2a) + 8 = 192
4a + 8 = 192
4a = 192 – 8
4a = 184
a = 184 : 4
a = 46.
Vậy 3 số chẵn đó là 46, 48, 50.
a) x2 + 2x + 1 = x2 + 2.x.1 + 12 = (x + 1)2 (Áp dụng hằng đẳng thức (1) với A = x và B = 1)
b) 9x2 + y2 + 6xy = 9x2 + 6xy + y2 = (3x)2 + 2.3x.y + y2
= (3x + y)2 (Áp dụng hằng đẳng thức (1) với A = 3x và B = y)
c) 25a2 + 4b2 – 20ab = 25a2 – 20ab + 4b2 = (5a)2 – 2.5a.2b + (2b)2
= (5a – 2b)2 (Áp dụng hằng đẳng thức (2) với A = 5a và B = 2b)
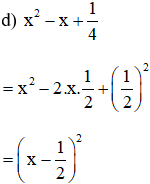
(Áp dụng hằng đẳng thức (2) với A = x và 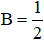
(10a + 5)2 = (10a)2 + 2.10a.5 + 52 = 100a2 + 100a + 25 = 100a(a + 1) + 25
Đặt A = a.(a + 1). Khi đó ta có:
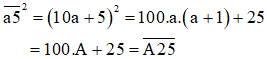
Do vậy, để tính bình phương của một số tự nhiên có dạng 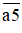
Áp dụng:
252 = (10.2 + 5)2 do đó a = 2 ⇒ A = a(a + 1) = 2.3 = 6
sau đó viết 25 vào đằng sau ta được 625. Vậy 252 = 625
352 = (10.3 + 5)2 do đó a = 3 ⇒ A = a(a + 1) = 3.4 = 12
sau đó viết 25 vào đằng sau ta được 1225. Vậy 352 = 1225
652 = (10.6 + 5)2 do đó a = 6 ⇒ A = a(a + 1) = 6.7 = 42
sau đó viết 25 vào đằng sau ta được 4225. Vậy 652 = 4225
752 = (10.7 + 5)2 do đó a = 7 ⇒ A = a(a + 1) = 7.8 = 56
sau đó viết 25 vào đằng sau ta được 5625. Vậy 752 = 5625
a) Dễ dàng nhận thấy đây là hằng đẳng thức (1) với A = x ;
2.AB = 6xy ⇒ B = 3y.
Vậy ta có hằng đẳng thức: x2 + 2.x.3y + (3y)2 = (x + 3y)2
hay x2 + 6xy + 9y2 = (x + 3y)2
b) Nhận thấy đây là hằng đẳng thức (2) với : B2 = 25y2 = (5y)2 ⇒ B = 5y
2.AB = 10xy = 2.x.5y ⇒ A = x.
Vậy ta có hằng đẳng thức : x2 – 10xy + 25y2 = (x – 5y)2
c) Đề bài tương tự: 4x2 + 4xy + ... = (... + y2)
... – 8xy + y2 = ( ...– ...)2
Diện tích của miếng tôn phải cắt là : (a – b)2.
Phần diện tích còn lại (a + b)2 – (a – b)2.
Ta có: (a + b)2 – (a – b)2 = (a2 + 2ab + b2) – ( a2 – 2ab + b2 )
= a2 + 2ab + b2 – a2 + 2ab – b2 = 4ab
Hoặc: (a + b)2 – (a – b)2 = [(a + b) + (a – b)].[(a + b) – (a – b)] (Áp dụng hằng đẳng thức (3))
= 2a.2b = 4ab.
Vậy phần diện tích hình còn lại là 4ab và không phụ thuộc vào vị trí cắt.
Ta có: (x + 2y)2 = x2 + 2.x.2y + 4y2 = x2 + 4xy + 4y2 ≠ x2 + 2xy + 4y2.
a) 9x2 – 6x + 1 = (3x)2 – 2.3x.1 + 12
= (3x – 1)2 (Áp dụng hằng đẳng thức (2) với A = 3x; B = 1)
b) (2x + 3y)2 + 2.(2x + 3y) + 1 = (2x + 3y)2 + 2.(2x + 3y).1 + 12
= [(2x + 3y) +1]2 (Áp dụng hằng đẳng thức (1) với A = 2x + 3y ; B = 1)
= (2x + 3y + 1)2
c) Đề bài tương tự: Viết các đa thức sau dưới dạng bình phương của một tổng hoặc hiệu :
4x2 – 12x + 9
(2a + b)2 – 4.(2a + b) + 4.
a) 1012 = (100 + 1)2 = 1002 + 2.100 + 1 = 10000 + 200 + 1 = 10201
b) 1992 = (200 – 1)2 = 2002 – 2.200 + 1 = 40000 – 400 + 1 = 39601
c) 47.53 = (50 – 3)(50 + 3) = 502 – 32 = 2500 – 9 = 2491.
+ Chứng minh (a + b)2 = (a – b)2 + 4ab
Ta có: VP = (a – b)2 + 4ab = a2 – 2ab + b2 + 4ab = a2 + (4ab – 2ab) + b2
= a2 + 2ab + b2 = (a + b)2 = VT (đpcm)
+ Chứng minh (a – b)2 = (a + b)2 – 4ab
Ta có: VP = (a + b)2 – 4ab = a2 + 2ab + b2 – 4ab = a2 + (2ab – 4ab) + b2 = a2 – 2ab + b2
= (a – b)2 = VT (đpcm)
+ Áp dụng, tính:
a) (a – b)2 = (a + b)2 – 4ab = 72 – 4.12 = 49 – 48 = 1
b) (a + b)2 = (a – b)2 + 4ab = 202 + 4.3 = 400 + 12 = 412.
a) Với x = 5: A = (7.5 – 5)2 = 302 = 900
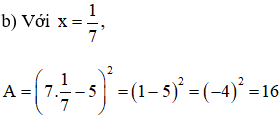
a) (a + b + c)2 = [(a + b) + c]2 = (a + b)2 + 2(a + b)c + c2
= a2 + 2ab + b2 + 2ac + 2bc + c2 = a2 + b2 + c2 + 2ab + 2bc + 2ac
b) (a + b – c)2 = [(a + b) – c]2 = (a + b)2 – 2(a + b)c + c2
= a2 + 2ab + b2 – 2ac – 2bc + c2 = a2 + b2 + c2 + 2ab – 2bc – 2ac
c) (a – b – c)2 = [(a – b) – c]2 = (a – b)2 – 2(a – b)c + c2
= a2 – 2ab + b2 – 2ac + 2bc + c2 = a2 + b2 + c2 – 2ab + 2bc – 2ac.
Hướng dẫn giải.
a) (2x2 + 3y)3 = (2x2)3 + 3.(2x2)2.3y + 3.2x2.(3y)2 + (3y)3
(Áp dụng HĐT (4) với A = 2x2, B = 3y)
= 8x6 + 3.4x4.3y + 3.2x2.9y2 + 27y3 = 8x6 + 36x4y + 54x2y2 + 27y3
b)
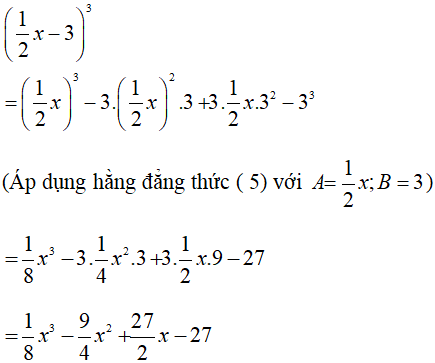
a) –x3 + 3x2 – 3x + 1 = (–x)3 + 3.(–x)2.1 + 3.(–x).1 + 13
= (–x + 1)3 (Áp dụng HĐT (4) với A = –x và B = 1)
b) 8 – 12x + 6x2 – x3 = 23 – 3.22.x + 3.2.x2 – x3
= (2 – x)3 (Áp dụng HĐT (5) với A = 2 và B = x)
a) x3 + 12x2 + 48x + 64 = x3 + 3.x2.4 + 3.x.42 + 43 = (x + 4)3
Tại x = 6, giá trị biểu thức bằng (6 + 4)3 = 103 = 1000.
b) x3 – 6x2 + 12x – 8 = x3 – 3.x2.2 + 3.x.22 – 23 = (x – 2)3
Tại x = 22, giá trị biểu thức bằng (22 – 2)3 = 203 = 8000.
N x3 – 3x2 + 3x – 1 = x3 – 3.x2.1 + 3.x.12 – 13 = (x – 1)3
U 16 + 8x + x2 = 42 + 2.4.x + x2 = (4 + x)2 = (x + 4)2
H 3x2 + 3x + 1 + x3 = x3 + 3x2 + 3x + 1 = (x + 1)3 = (1 + x)3
 1 – 2y + y2 = 12 – 2.1.y + y2 = (1 – y)2 = (y – 1)2
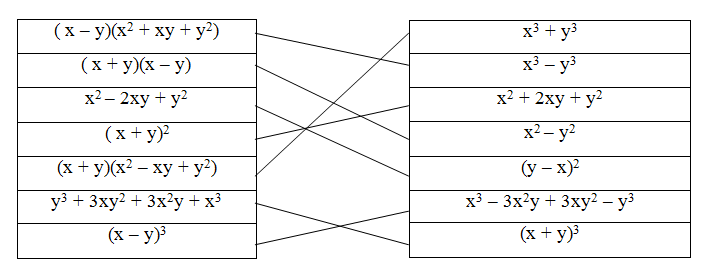
Điền vào bảng như sau:
| (x – 1)3 | (x + 1)3 | (y – 1)2 | (x – 1)3 | (1 + x)3 | (1 – y)2 | (x + 4)2 |
| N | H | Â | N | H | Â | U |
Vậy: Đức tính đáng quý là "NHÂN HẬU"
(Chú ý: Bạn có thể làm theo cách ngược lại, tức là khai triển các biểu thức (x – 1)3, (x + 1)3, (y – 1)2, (x + 4)2 … để tìm xem kết quả ứng với chữ nào và điền vào bảng.)
a) (x + 3)(x2 – 3x + 9) – (54 + x3) = x3 + 33 – (54 + x3) (Áp dụng HĐT (6) với A = x và B = 3)
= x3 + 27 – 54 – x3 = –27
b) (2x + y)(4x2 – 2xy + y2) – (2x – y)(4x2 + 2xy + y2)
= (2x + y)[(2x)2 – 2x.y + y2] – (2x – y)[(2x)2 + 2x.y + y2]
= [(2x)3 + y3] – [(2x)3 – y3] = (2x)3 + y3 – (2x)3 + y3 = 2y3
a) Biến đổi vế phải ta được: (a + b)3 – 3ab(a + b)
= a3 + 3a2b + 3ab2 + b3 – 3a2b – 3ab2 = a3 + b3
Vậy a3 + b3 = (a + b)3 – 3ab(a + b)
b) Biến đổi vế phải ta được: (a – b)3 + 3ab(a – b)
= a3 – 3a2b + 3ab2 – b3 + 3a2b – 3ab2 = a3 – b3
Vậy a3 – b3 = (a – b)3 + 3ab(a – b)
– Áp dụng: Với ab = 6, a + b = –5, ta được:
a3 + b3 = (a + b)3 – 3ab(a + b) = (–5)3 – 3.6.(–5) = –53 + 3.6.5 = –125 + 90 = –35
a) Ta có thể nhận thấy đây là hằng đẳng thức (6).
27x3 + y3 = (3x)3 + y3 = (3x + y)[(3x)2 – 3x.y + y2] (Áp dụng HĐT (6) với A = 3x, B = y)
= (3x + y)(9x2 – 3xy + y2)
Vậy ta cần điền :
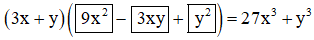
b) Ta có thể nhận thấy đây là hằng đẳng thức (7)
8x3 – 125 = (2x)3 – 53 = (2x – 5).[(2x)2 + (2x).5 + 52] (Áp dụng HĐT (7) với A = 2x, B = 5)
= (2x – 5).(4x2 + 10x + 25)
Vậy ta cần điền :
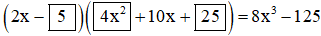
a) (2 + xy)2 = 22 + 2.2.xy + (xy)2 (Áp dụng HĐT (1)) = 4 + 4xy + x2y2
b) (5 – 3x)2 = 52 – 2.5.3x + (3x)2 (Áp dụng HĐT (2)) = 25 – 30x + 9x2
c) (5 – x2)(5 + x2) = 52 – (x2)2 (Áp dụng HĐT (3)) = 25 – x4
d) (5x – 1)3 = (5x)3 – 3.(5x)2.1 + 3.5x.12 – 13 (Áp dụng HĐT (5)) = 125x3 – 75x2 + 15x – 1
e) (2x – y).(4x2 + 2xy + y2) = (2x – y).[(2x)2 + 2x.y + y2] = (2x)3 – y3 (Áp dụng HĐT (7))
= 8x3 – y3
f) (x + 3)(x2 – 3x + 9) = (x + 3)(x2 – x.3 + 32) = x3 + 33 (Áp dụng HĐT (6)) = x3 + 27
a) (a + b)2 – (a – b)2 = [(a + b) – (a – b)].[(a + b) + (a – b)]
= [a + b - a + b].[a + b + a - b] = 2b.2a = 4ab
b) (a + b)3 – (a – b)3 – 2b3
= (a3 + 3a2b + 3ab2 + b3) – (a3 – 3a2b + 3ab2 – b3) – 2b3 (Áp dụng HĐT (4) và (5))
= a3 + 3a2b + 3ab2 + b3 – a3 + 3a2b – 3ab2 + b3 – 2b3
= (a3 – a3) + (3a2b + 3a2b) + (3ab2 – 3ab2) + (b3 + b3 – 2b3) = 6a2b
c) (x + y + z)2 – 2.(x + y + z).(x + y) + (x + y)2
= [(x + y + z) – (x + y)]2 (Áp dụng HĐT (2) với A = x + y + z ; B = x + y) = z2.
a) 342 + 662 + 68.66 = 342 + 68.66 + 662 = 342 + 2.34.66 + 662
= (34 + 66)2 = 1002 = 10000
b) 742 + 242 – 48.74 = 742 – 48.74 + 242 = 742 – 2.74.24 + 242
= (74 – 24)2 = 502 = 2500
a) x2 + 4x + 4 = x2 + 2.x.2 + 22 = (x + 2)2
Tại x = 98, giá trị biểu thức bằng (98 + 2)2 = 1002 = 10000
b) x3 + 3x2 + 3x + 1 = x3 + 3.x2.1 + 3.x.12 + 13 = (x + 1)3
Tại x = 99, giá trị biểu thức bằng (99 + 1)3 = 1003 = 1000000
a) Sử dụng tính chất hai số đối nhau:
(a – b)3 = [(–1)(b – a)]3 =(–1)3(b – a)3 = –1.(b – a)3 = –(b – a)3 (đpcm)
b) (–a – b)2 = [(– 1).(a + b)]2 = (–1)2(a + b)2 = 1.(a + b)2 = (a + b)2 (đpcm)
Hướng dẫn giải.
a) 3x – 6y = 3.x – 3.2y (Xuất hiện nhân tử chung là 3) = 3(x – 2y)
c) 14x2y – 21xy2 + 28x2y2 = 7xy.2x – 7xy.3y + 7xy.4xy (Xuất hiện nhân tử chung 7xy)
= 7xy(2x – 3y + 4xy)
e) 10x(x – y) – 8y(y – x)
(Nhận thấy x – y = –(y – x) nên ta đổi y – x về x – y)
= 10x(x – y) – 8y[–(x – y)] = 10x(x – y) + 8y(x – y) = 2(x – y).5x + 2(x – y).4y
(Xuất hiện nhân tử chung 2(x – y))
= 2(x – y)(5x + 4y)
* Lưu ý: Nhiều khi, để xuất hiện nhân tử chung, ta cần biến đổi A = –(–A)
a) 15.91,5 + 150.0,85 = 15.91,5 + 15.10.0,85 = 15.91,5 + 15.8,5 = 15(91,5 + 8,5)
= 15.100 = 1500
b) x(x – 1) – y(1 – x) = x(x – 1) – y[–(x – 1)] = x(x – 1) + y(x – 1) = (x – 1)(x + y)
Tại x = 2001, y = 1999, giá trị biểu thức bằng:
(2001 – 1)(2001 + 1999) = 2000.4000 = 8000000
a) 5x(x – 2000) – x + 2000 = 0 ⇔ 5x(x – 2000) – (x – 2000) = 0
(Có x – 2000 là nhân tử chung)
⇔ (x – 2000).(5x – 1) = 0 ⇔ x – 2000 = 0 hoặc 5x – 1 = 0
+ x – 2000 = 0 ⇔ x = 2000
+ 5x – 1 = 0 ⇔ 5x = 1 ⇔ x = 1/5.
Vậy có hai giá trị của x thỏa mãn là x = 2000 và x = 1/5.
b) x3 = 13x ⇔ x3 – 13x = 0 ⇔ x.x2 – x.13 = 0 (Có nhân tử chung x)
⇔ x(x2 – 13) = 0 ⇔ x = 0 hoặc x2 – 13 = 0
+ x2 – 13 = 0 ⇔ x2 = 13 ⇔ x = √13 hoặc x = –√13
Vậy có ba giá trị của x thỏa mãn là x = 0, x = √13 và x = –√13.
Vì 54 chia hết cho 54 nên 55n.54 luôn chia hết cho 54 với mọi số tự nhiên n.
Vậy 55n + 1 – 55n chia hết cho 54.
a) x2 + 6x + 9 = x2 + 2.x.3 + 32 (Xuất hiện hằng đẳng thức (1)) = (x + 3)2
b) 10x – 25 – x2 = –(–10x + 25 + x2) = –(25 – 10x + x2) = –(52 – 2.5.x + x2)
(Xuất hiện hằng đẳng thức (2) trong ngoặc)
= –(5 – x)2
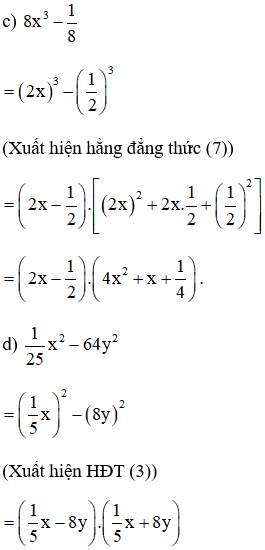
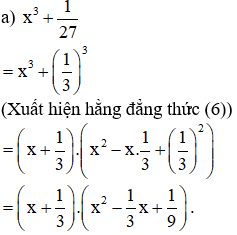
b) (a + b)3 – (a – b)3 (Xuất hiện hằng đẳng thức (7))
= [(a + b) – (a – b)][(a + b)2 + (a + b).(a – b) + (a – b)2]
= (a + b – a + b)(a2 + 2ab + b2 + a2 – b2+ a2 – 2ab + b2) = 2b.(3a2+ b2)
c) (a + b)3 + (a – b)3 (Xuất hiện hằng đẳng thức (6))
= [(a + b) + (a – b)][(a + b)2 – (a + b)(a –b) + (a – b)2]
= [(a + b) + (a – b)][(a2 + 2ab + b2) – (a2 – b2) + (a2 – 2ab + b2)]
= (a + b + a – b)(a2 + 2ab + b2 – a2 + b2 + a2 – 2ab + b2) = 2a.(a2 + 3b2)
d) 8x3 + 12x2y + 6xy2 + y3 = (2x)3 + 3.(2x)2.y + 3.2x.y2 + y3 (Xuất hiện hằng đẳng thức (4))
= (2x + y)3
e) –x3 + 9x2 – 27x + 27 = (–x)3 + 3.(–x)2.3 + 3.(–x).32 + 33 (Xuất hiện Hằng đẳng thức (4))
= (–x + 3)3 = (3 – x)3
a) Cách 1:

Cách 2: 2 – 25x2 = 0 ⇔ (√2)2 – (5x)2 = 0 (Xuất hiện hằng đẳng thức (3))
⇔ (√2 – 5x)(√2 + 5x) = 0 ⇔√2 – 5x = 0 hoặc √2 + 5x = 0
+ √2 – 5x = 0 ⇔ 5x = √2 ⇔ x = √2/5
+ √2 + 5x = 0 ⇔ 5x = –√2 ⇔ x = –√2/5
Vậy có hai giá trị của x thỏa mãn là
a) 732 – 272 = (73 + 27)(73 – 27) = 100.46 = 4600
b) 372 – 132 = (37 + 13)(37 – 13) = 50.24 = 100.12 = 1200
c) 20022 – 22 = (2002 + 2)(2002 – 2) = 2004 .2000 = 4008000
a) Cách 1: Nhóm hai hạng tử thứ 1 và thứ 2, hạng tử thứ 3 và thứ 4
x2 – xy + x – y = (x2 – xy) + (x – y) (Nhóm thứ nhất có nhân tử chung là x)
= x(x – y) + (x – y) (Xuất hiện nhân tử chung x – y)
= (x + 1)(x – y)
Cách 2: Nhóm hạng tử thứ 1 và thứ 3 ; hạng tử thứ 2 và thứ 4
x2 – xy + x – y = (x2 + x) – (xy + y)
(nhóm thứ nhất có nhân tử chung là x ; nhóm thứ hai có nhân tử chung là y)
= x.(x + 1) – y.(x + 1) (Xuất hiện nhân tử chung x + 1)
= (x – y)(x + 1)
b) xz + yz – 5(x + y) = (xz + yz) – 5(x + y)
(Nhóm thứ nhất có nhân tử chung là z ; nhóm thứ hai có nhân tử chung là 5)
= z(x + y) – 5(x + y) (Xuất hiện nhân tử chung là x + y)
= (z – 5)(x + y)
c) Cách 1: Nhóm hai hạng tử đầu tiên với nhau và hai hạng tử cuối với nhau:
3x2 – 3xy – 5x + 5y = (3x2 – 3xy) – (5x – 5y)
(Nhóm thứ nhất có nhân tử chung là 3x ; nhóm thứ hai có nhân tử chung là 5)
= 3x(x – y) – 5(x – y) (Xuất hiện nhân tử chung là (x – y))
= (x – y)(3x – 5)
Cách 2: Nhóm hạng tử thứ 1 với hạng tử thứ 3; hạng tử thứ 2 với hạng tử thứ 4:
3x2 – 3xy – 5x + 5y = (3x2 – 5x) – (3xy – 5y)
(Nhóm thứ nhất có nhân tử chung là x, nhóm thứ hai có nhân tử chung là y)
= x.(3x – 5) – y.(3x – 5) (Xuất hiện nhân tử chung 3x – 5)
= (x – y).(3x – 5).
a) Nhận thấy x2 + 4x + 4 là hằng đẳng thức nên ta nhóm với nhau.
x2 + 4x – y2 + 4 = (x2 + 4x + 4) – y2 = (x + 2)2 – y2 (Xuất hiện hằng đẳng thức (3))
= (x + 2 – y)(x + 2 + y)
b) 3x2 + 6xy + 3y2 – 3z2 = 3.(x2 + 2xy + y2 – z2)
(Nhận thấy xuất hiện x2 + 2xy + y2 là hằng đẳng thức nên ta nhóm với nhau)
= 3[(x2 + 2xy + y2) – z2] = 3[(x + y)2 – z2] = 3(x + y – z)(x + y + z)
c) x2 – 2xy + y2 – z2 + 2zt – t2
(Nhận thấy x2 – 2xy + y2 và z2 – 2zt + t2 là các hằng đẳng thức)
= (x2 – 2xy + y2) – (z2 – 2zt + t2) = (x – y)2 – (z – t)2 (xuất hiện hằng đẳng thức (3))
= [(x – y) – (z – t)][(x – y) + (z – t)] = (x – y – z + t)(x – y + z –t)
a) 37,5.6,5 – 7,5.3,4 – 6,6.7.5 + 3,5.37,5
(Hạng tử đầu tiên và cuối cùng đều có nhân tử 37,5; hai hạng tử giữa đều có nhân tử 7,5)
= (37,5.6,5 + 3,5.37,5) – (7,5.3,4 + 6,6.7,5) = 37,5(6,5 + 3,5) – 7,5(3,4 + 6,6)
= 37,5.10 – 7,5.10 = 375 – 75 = 300
b) 452 + 402 – 152 + 80.45 = 452 + 80.45 + 402 – 152 = 452 + 2.45.40 + 402 – 152
= (45 + 40)2 – 152 = 852 – 152 = (85 – 15)(85 + 15) = 70.100 = 7000
a) x(x – 2) + x – 2 = 0 (Xuất hiện nhân tử chung x – 2)
⇔ (x – 2)(x + 1) = 0 ⇔ x – 2 = 0 hoặc x + 1 = 0
+ x – 2 = 0 ⇔ x = 2
+ x + 1 = 0 ⇔ x = –1
Vậy x = – 1 hoặc x = 2.
b) 5x(x – 3) – x + 3 = 0 ⇔ 5x(x – 3) – (x – 3) = 0 (Xuất hiện nhân tử chung x – 3)
⇔ (x – 3)(5x – 1) = 0 ⇔ x – 3 = 0 hoặc 5x – 1= 0
+ x – 3 = 0 ⇔ x = 3
+ 5x – 1 = 0 ⇔ 5x = 1 ⇔ x = 1/5
Vậy x = 3 hoặc x = 1/5.
a) x3 – 2x2 + x = x.x2 – x.2x + x (Xuất hiện nhân tử chung là x)
= x(x2 – 2x + 1) (Xuất hiện hằng đẳng thức (2))
= x(x – 1)2
b) 2x2 + 4x + 2 – 2y2 (có nhân tử chung là 2)
= 2.(x2 + 2x + 1 – y2) (Xuất hiện x2 + 2x + 1 là hằng đẳng thức)
= 2[(x2 + 2x + 1) – y2] = 2[(x + 1)2 – y2] (Xuất hiện hằng đẳng thức (3))
= 2(x + 1 – y)(x + 1 + y)
c) 2xy – x2 – y2 + 16 (Có 2xy ; x2 ; y2, ta liên tưởng đến HĐT (1) hoặc (2))
= 16 – (x2 – 2xy + y2) = 42 – (x – y)2 (xuất hiện hằng đẳng thức (3))
= [4 – (x – y)][4 + (x - y)] = (4 – x + y)(4 + x – y).
(5n + 2)2 – 4 = (5n + 2)2 – 22 = (5n + 2 – 2)(5n + 2 + 2) = 5n(5n + 4)
Vì 5 ⋮ 5 nên 5n(5n + 4) ⋮ 5 ∀n ∈ Ζ.
Vậy (5n + 2)2 – 4 luôn chia hết cho 5 với n ∈ Ζ
Cách 1: Tách một hạng tử thành tổng hai hạng tử để xuất hiện nhân tử chung.
x2 – 3x + 2 = x2 – x – 2x + 2 (Tách –3x = – x – 2x)
= (x2 – x) – (2x – 2) = x(x – 1) – 2(x – 1) (Có x – 1 là nhân tử chung)
= (x – 1)(x – 2)
Hoặc: x2 – 3x + 2 = x2 – 3x – 4 + 6 (Tách 2 = – 4 + 6)
= x2 – 4 – 3x + 6 = (x2 – 22) – 3(x – 2)
= (x – 2)(x + 2) – 3.(x – 2) (Xuất hiện nhân tử chung x – 2)
= (x – 2)(x + 2 – 3) = (x – 2)(x – 1)
b) x2 + x – 6 = x2 + 3x – 2x – 6 (Tách x = 3x – 2x)
= x(x + 3) – 2(x + 3) (có x + 3 là nhân tử chung)
= (x + 3)(x – 2)
c) x2 + 5x + 6 (Tách 5x = 2x + 3x) = x2 + 2x + 3x + 6
= x(x + 2) + 3(x + 2) (Có x + 2 là nhân tử chung) = (x + 2)(x + 3)
Cách 2: Đưa về hằng đẳng thức (1) hoặc (2)
a) x2 – 3x + 2
(Vì có x2 và 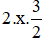
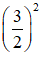
= (x – 2)(x – 1)
b) x2 + x - 6
= (x – 2)(x + 3).
c) x2 + 5x + 6
= (x + 2)(x + 3).
Hướng dẫn giải.
a) x3 + 2x2y + xy2 – 9x (Có x là nhân tử chung)
= x(x2 + 2xy + y2 – 9) (Có x2 + 2xy + y2 là hằng đẳng thức)
= x[(x2 + 2xy + y2) – 9] = x[(x + y)2 – 32] (Xuất hiện hằng đẳng thức (3)]
= x(x + y – 3)(x + y + 3)
b) 2x – 2y – x2 + 2xy – y2 (Có x2 ; 2xy ; y2 ta liên tưởng đến HĐT (1) hoặc (2))
= (2x – 2y) – (x2 – 2xy + y2) = 2(x – y) – (x – y)2 (Có x – y là nhân tử chung)
= (x – y)[2 – (x – y)] = (x – y)(2 – x + y)
c) x4 – 2x2 (Có x2 là nhân tử chung) = x2(x2 – 2)
b) Có: (2x – 1)2 – (x + 3)2 (xuất hiện HĐT (3))
= [(2x – 1) – (x + 3)][(2x – 1) + (x + 3)] = (2x – 1 – x – 3).(2x – 1 + x + 3) = (x – 4)(3x + 2)
Vậy (2x – 1)2 – (x + 3)2 = 0 ⇔ (x – 4)(3x + 2) = 0
⇔ x – 4 = 0 hoặc 3x + 2 = 0 ⇔ x = 4 hoặc x = –2/3
Vậy x = 4 hoặc x = –2/3.
c) Có: x2(x – 3) + 12 – 4x = x2(x – 3) – 4.(x – 3) (Có nhân tử chung là x – 3)
= (x2 – 4)(x – 3) = (x2 – 22).(x – 3) (Xuất hiện HĐT (3)) = (x – 2)(x + 2)(x – 3)
Vậy x2(x – 3) + 12 – 4x = 0 ⇔ (x – 2)(x + 2)(x – 3) = 0
⇔ x – 2 = 0 hoặc x + 2 = 0 hoặc x – 3 = 0 ⇔ x = 2 hoặc x = –2 hoặc x = 3.
Vậy x = 2 hoặc x = –2 hoặc x = 3.
a) Ta có:
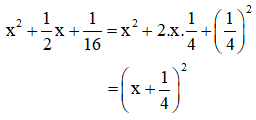
Do đó tại x = 49,75, giá trị biểu thức bằng
b) Ta có: x2 – y2 – 2y – 1 (Thấy có y2 ; 2y ; 1 ta liên tưởng đến HĐT (1) hoặc (2))
= x2 – (y2 + 2y + 1) = x2 – (y + 1)2 (Xuất hiện HĐT (3)) = (x – y – 1)(x + y + 1)
Với x = 93, y = 6 thì: (93 – 6 – 1)(93 + 6 + 1) = 86.100 = 8600
a) Cách 1: x2 – 4x + 3 = x2 – x – 3x + 3 (Tách –4x = –x – 3x)
= x(x – 1) – 3(x – 1) (Có x – 1 là nhân tử chung) = (x – 1)(x – 3)
Cách 2: x2 – 4x + 3 = x2 – 2.x.2 + 22 + 3 – 22 (Thêm bớt 22 để có HĐT (2))
= (x – 2)2 – 1 (Xuất hiện HĐT (3)) = (x – 2 – 1)(x – 2 + 1) = (x – 3)(x – 1)
b) x2 + 5x + 4 = x2 + x + 4x + 4 (Tách 5x = x + 4x)
= x(x + 1) + 4(x + 1) (có x + 1 là nhân tử chung) = (x + 1)(x + 4)
c) x2 – x – 6 = x2 + 2x – 3x – 6 (Tách –x = 2x – 3x)
= x(x + 2) – 3(x + 2) (có x + 2 là nhân tử chung) = (x – 3)(x + 2)
d) x4 + 4 = (x2)2 + 22 = x4 + 2.x2.2 + 4 – 4x2 (Thêm bớt 2.x2.2 để có HĐT (1))
= (x2 + 2)2 – (2x)2 (Xuất hiện HĐT (3)) = (x2 + 2 – 2x)(x2 + 2 + 2x)
= n(n2 – 1) (Xuất hiện HĐT (3)) = n(n – 1)(n + 1)
n – 1; n và n + 1 là ba số tự nhiên liên tiếp nên
+ Trong đó có ít nhất một số chẵn ⇒ (n – 1).n.(n + 1) ⋮ 2
+ Trong đó có ít nhất một số chia hết cho 3 ⇒ (n – 1).n.(n + 1) ⋮ 3
Vậy A ⋮ 2 và A ⋮ 3 nên A ⋮ 6.
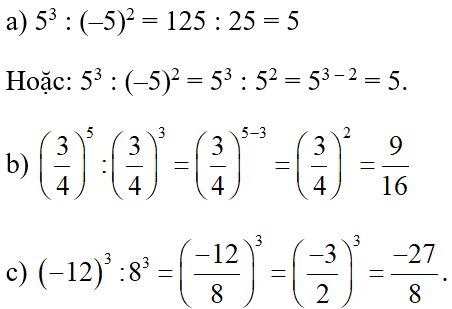
a) x10 : (-x)8 = x10 : x8 = x10 – 8 = x2 Vì (-x)8 = (-1.x)8 = (-1)8.x8 = x8
b) (-x)5 : (-x)3 = (-x)5 – 3 = (-x)2 = x2 Vì (-x)2 = (-1.x)2 = (-1)2.x2 = x2
c) (-y)5 : (-y)4 = (-y)5 – 4 = (–y)1 = - y
a) 5x2y4 : 10x2y = (5 : 10).(x2 : x2).(y4 : y) (Chia hệ số cho hệ số, chia lũy thừa của từng biến)
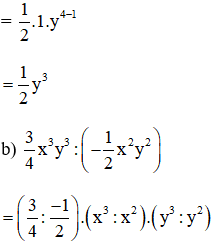
(Chia hệ số cho hệ số, chia lũy thừa của từng biến)
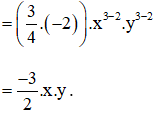
c) (–xy)10 : (–xy)5 = (–xy)10 – 5 = (–xy)5
= 3.x4 – 1.y3 – 2 . 1 = 3x3y
Tại x = 2 ; y = –10 và z = 2004, giá trị biểu thức bằng : 3.23.(–10) = –240.
15xy2 chia hết cho 6y2
17xy3 chia hết cho 6y2
18y2 chia hết cho 6y2
Vậy A = 15xy2 + 17xy3 + 18y2 chia hết cho 6y2 hay A chia hết cho B.
a) (–2x5 + 3x2 – 4x3) : 2x2 = (–2x5) : 2x2 + 3x2 : 2x2 + (–4x3) : 2x2
= [(–2) : 2].(x5 : x2) + (3 : 2).(x2 : x2) + [(–4) : 2].(x3 : x2)
=
c) (3x2y2 + 6x2y3 – 12xy) : 3xy = (3x2y2 : 3xy) + (6x2y3 : 3xy) + ( –12xy : 3xy)
= (3 : 3).(x2 : x).(y2 : y) + (6 : 3).(x2 : x).(y3 : y) + (–12 : 3).(x : x).(y : y)
= 1.x.y + 2.xy2 + (–4).1.1 = xy + 2xy2 – 4
Đặt x – y = z, Khi đó biểu thức trở thành : (3z4 + 2z3 – 5z2) : z2
= 3z4 : z2 + 2z3 : z2 + (–5z2) : z2 = 3.(z4 : z2) + 2.(z3 : z2) + (–5).(z2 : z2)
= 3.z2 + 2.z + (–5).1 = 3z2 + 2z – 5
Thay trả lại z = x – y ta được kết quả biểu thức bằng : 3(x – y)2 + 2(x – y) – 5.
Vì 5x4 chia hết cho 2x2;
–4x3 chia hết cho 2x2;
6x2y chia hết cho 2x2
Do đó A = 5x4 – 4x3 + 6x2y chia hết cho 2x2 hay A chia hết cho B.
Chú ý: Đơn thức A chia hết cho đơn thức B nếu tìm được đơn thức Q sao cho A=B.Q
Ví dụ : Cho hai đơn thức A= 2x2y3; B = 7xy
Khi đó với đơn thức 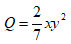
Do đó, đơn thức A chia hết cho đơn thức B.
a) x3 – 7x + 3 – x2 = x3 – x2 – 7x + 3
Thực hiện phép chia:
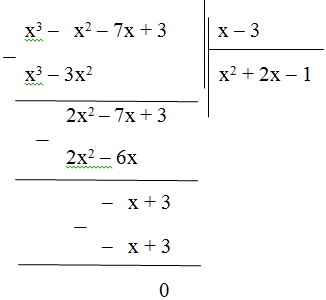
Vậy (x3 – x2 – 7x + 3) : (x – 3) = x2 + 2x – 1
b) 2x4 – 3x3 – 3x2 – 2 + 6x = 2x4 – 3x3 – 3x2 + 6x – 2
Thực hiện phép chia:
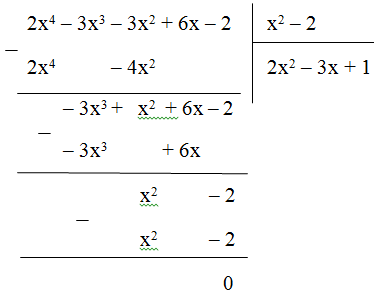
Vậy (2x4 – 3x3 – 3x2 + 6x – 2) : (x2 – 2) = 2x2 – 3x + 1.
a) (x2 + 2xy + y2) : (x + y) = (x + y)2 : (x + y) = x + y
b) (125x3 + 1) : (5x + 1) = [(5x)3 + 1] : (5x + 1) = (5x + 1)[(5x)2 – 5x + 1]] : (5x + 1)
= (5x)2 – 5x + 1 = 25x2 – 5x + 1
c) (x2 – 2xy + y2) : (y – x) = (x – y)2 : [-(x – y)] = -(x – y) = y – x
Hoặc (x2 – 2xy + y2) : (y – x) = (y2 – 2yx + x2) : (y – x) = (y – x)2 : (y – x) = y – x
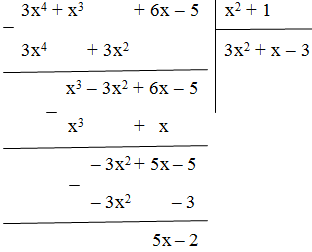
Vậy 3x4 + x3 + 6x – 5 = (x2 + 1).(3x2 + x – 3) + 5x – 2.
Hướng dẫn giải.
a) (25x5 – 5x4 + 10x2) : 5x2 = 25x5 : 5x2 + (-5x4) : 5x2 + 10x2 : 5x2
= (25 : 5).(x5 : x2) + (-5 : 5).(x4 : x2) + (10 : 5).(x2 : x2) = 5.x5 – 2 + (-1).x4 – 2 + 2.1
= 5x3 – x2 + 2
b) (15x3y2 – 6x2y – 3x2y2) : 6x2y = (15x3y2 : 6x2y) + (-6x2y) : 6x2y + (-3x2y2) : 6x2y
= (15 : 6).(x3 : x2).(y2 : y) + (-6 : 6).(x2 : x2).(y : y) + (-3 : 6).(x2 : x2).(y2 : y)
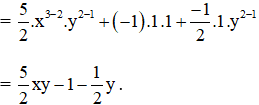
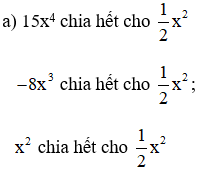
Do đó A = 15x4 - 8x3 + x2 chia hết cho 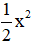
b) A = x2 - 2x + 1 = (x – 1)2
Vậy A chia hết cho x – 1 hay A chia hết cho B.
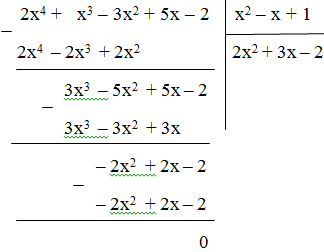
Vậy (2x4 + x3 – 3x2 + 5x – 2) : (x2 – x + 1) = 2x2 + 3x - 2
a) (4x2 – 9y2) : (2x – 3y) (Sử dụng HĐT để phân tích số bị chia thành tích)
= [(2x)2 – (3y)2] : (2x – 3y) (Xuất hiện hằng đẳng thức (3))
= (2x – 3y)(2x + 3y) : (2x – 3y) = 2x + 3y.
b) (27x3 – 1) : (3x – 1) (Sử dụng HĐT để phân tích số bị chia thành tích)
= [(3x)3 – 1] : (3x – 1) (Xuất hiện hằng đẳng thức (7))
= (3x – 1).[(3x)2 + 3x.1 + 12] : (3x – 1) = (3x – 1).(9x2 + 3x + 1) : (3x – 1)
= 9x2 + 3x + 1
c) (8x3 + 1) : (4x2 – 2x + 1) (Sử dụng HĐT để phân tích số bị chia thành tích)
= [(2x)3 + 1] : (4x2 – 2x + 1) (Xuất hiện HĐT (6))
= (2x + 1).[(2x)2 - 2x.1 + 12] : (4x2 – 2x + 1) = (2x + 1).(4x2 - 2x + 1) : (4x2 – 2x + 1)
= 2x + 1.
d) (x2 – 3x + xy – 3y) : (x + y) (Nhóm hạng tử để phân tích số bị chia thành tích)
= [(x2 – 3x) + (xy – 3y)] : (x + y) = [x.(x – 3) + y.(x – 3)] : (x + y)
= (x + y).(x – 3) : (x + y) = x – 3.
Cách 1: Thực hiện phép chia:

2x3 – 3x2 + x + a chia hết cho x + 2 ⇔ số dư = a – 30 = 0 ⇔ a = 30.
Cách 2: Phân tích 2x3 – 3x2 + x + a thành nhân tử có chứa x + 2.
2x3 – 3x2 + x + a = 2x3 + 4x2 – 7x2 – 14x + 15x + 30 + a – 30
(Tách -3x2 = 4x2 – 7x2; x = -14x + 15x)
= 2x2(x + 2) – 7x(x + 2) + 15(x + 2) + a – 30 = (2x2 – 7x + 15)(x + 2) + a – 30
2x3 – 3x2 + x + a chia hết cho x + 2 ⇔ a – 30 = 0 ⇔ a = 30.
a) 5x2.(3x2 – 7x + 2) = 5x2.3x2 + 5x2.(-7x) + 5x2.2 = (5.3).(x2.x2) + [5.(-7)].(x2.x) + (5.2).x2
= 15x2 + 2 + (-35).x2 + 1 + 10.x2 = 15x4 – 35x3 + 10x2
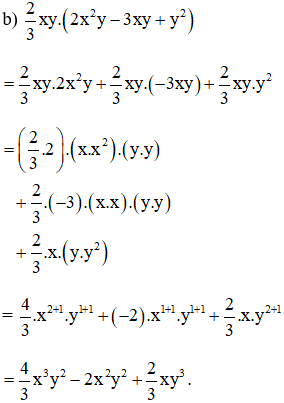
a) (2x2 – 3x)(5x2 – 2x + 1) = 2x2(5x2 – 2x + 1) + (-3x)(5x2 – 2x + 1)
= 2x2.5x2 + 2x2.(-2x) + 2x2.1 + (–3x).5x2 + (-3x).(-2x) + (-3x).1
= (2.5)(x2.x2) + (2. (-2)).(x2.x) + 2x2 + [(-3).5].(x.x2) + [(-3).(-2).(x.x) + (-3x)
= 10x4 – 4x3 + 2x2 – 15x3 + 6x2 – 3x = 10x4 – (4x3 + 15x3) + (2x2 + 6x2) – 3x
= 10x4 – 19x3 + 8x2 – 3x
b) (x – 2y)(3xy + 5y2 + x) = x.(3xy + 5y2 + x) + (-2y).(3xy + 5y2 + x)
= x.3xy + x.5y2 + x.x + (-2y).3xy + (–2y).5y2 + (–2y).x
= 3x2y + 5xy2 + x2 – 6xy2 – 10y3 – 2xy = 3x2y + (5xy2 – 6xy2) + x2 – 10y3 – 2xy
= 3x2y – xy2 + x2 – 10y3 – 2xy
a) M = x2 + 4y2 – 4xy = x2 – 2.x.2y + (2y)2 (Hằng đẳng thức (2)) = (x – 2y)2
Thay x = 18, y = 4 ta được: M = (18 – 2.4)2 = 102 = 100
b) N = 8x3 – 12x2y + 6xy2 – y3 = (2x)3 – 3(2x)2y + 3.2xy2 – y3 (Hằng đẳng thức (5))
= (2x – y)3
Thay x = 6, y = - 8 ta được: N = (2.6 – (-8))3 = 203 = 8000
a) (x + 2)(x – 2) – (x – 3)(x + 1) = x2 – 22 – (x2 + x – 3x – 3)
= x2 – 4 – x2 – x + 3x + 3 = 2x – 1
b) (2x + 1)2 + (3x – 1)2 + 2(2x + 1)(3x – 1) = (2x + 1)2 + 2.(2x + 1)(3x – 1) + (3x – 1)2
= [(2x + 1) + (3x – 1)]2 = (2x + 1 + 3x – 1)2 = (5x)2 = 25x2
a) Cách 1: x2 – 4 + (x – 2)2 (Xuất hiện hằng đẳng thức (3))
= (x2– 22) + (x – 2)2 = (x – 2)(x + 2) + (x – 2)2 (Có nhân tử chung x – 2)
= (x – 2)[(x + 2) + (x – 2)] = (x – 2)(x + 2 + x – 2) = (x – 2)(2x) = 2x(x – 2)
Cách 2: x2 – 4 + (x – 2)2 (Khai triển hằng đẳng thức (2))
= x2 – 4 + (x2 – 2.x.2 + 22) = x2 – 4 + x2 – 4x + 4 = 2x2 – 4x (Có nhân tử chung là 2x)
= 2x(x – 2)
b) x3 – 2x2 + x – xy2 (Có nhân tử chung x)
= x(x2 – 2x + 1 – y2) (Có x2 – 2x + 1 là hằng đẳng thức).
= x[(x – 1)2 – y2] (Xuất hiện hằng đẳng thức (3)) = x(x – 1 + y)(x – 1 – y)
c) x3 – 4x2 – 12x + 27 (Nhóm để xuất hiện nhân tử chung)
= (x3 + 27) – (4x2 + 12x) = (x3 + 33) – (4x2 + 12x)
(nhóm 1 là HĐT, nhóm 2 có 4x là nhân tử chung)
= (x + 3)(x2 – 3x + 9) – 4x(x + 3) = (x + 3)(x2 – 3x + 9 – 4x) = (x + 3)(x2 – 7x + 9)
a) Cách 1: Thực hiện phép chia
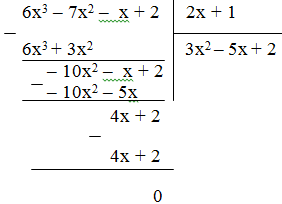
Vậy (6x3 – 7x2 – x + 2) : (2x + 1) = 3x2 – 5x + 2
Cách 2: Phân tích 6x3 – 7x2 – x + 2 thành (2x + 1).P(x) + R(x)
6x3 – 7x2 – x + 2 = 6x3 + 3x2 – 10x2 – 5x + 4x + 2 (Tách -7x2 = 3x2 – 10x2; -x = -5x + 4x)
= 3x2.(2x + 1) – 5x.(2x + 1) + 2.(2x + 1) = (3x2 – 5x + 2)(2x + 1)
Vậy (6x3 – 7x2 – x + 2) : (2x + 1) = 3x2 – 5x + 2
Giải thích cách tách:
Vì có 6x3 nên ta cần thêm 3x2 để có thể phân tích thành 3x2(2x + 1). Do đó ta tách -7x2 = 3x2 – 10x2.
Lại có -10x2 nên ta cần thêm -5x để có thể phân tích thành -5x(2x + 1). Do đó ta tách –x = -5x + 4x.
Có 4x, ta cần thêm 2 để có 2.(2x + 1) nên 2 không cần phải tách.
b)
Cách 1: Thực hiện phép chia
Vậy (x4 – x3 + x2 + 3x) : (x2 – 2x + 3) = x2 + x
Cách 2: Phân tích x4 – x3 + x2 + 3x thành nhân tử có chứa x2 + x
x4 – x3 + x2 + 3x = x.(x3 – x2 + x + 3) = x.(x3 – 2x2 + 3x + x2 – 2x + 3)
= x.[x.(x2 – 2x + 3) + (x2 – 2x + 3)] = x.(x + 1)(x2 – 2x + 3)
Vậy (x4 – x3 + x2 + 3x) : (x2 – 2x + 3) = x(x + 1)
c) Phân tích số bị chia thành nhân tử, trong đó có nhân tử là số chia.
(x2 – y2 + 6x + 9) : (x + y + 3) (Có x2 + 6x + 9 là hằng đẳng thức)
= (x2 + 6x + 9 – y2) : (x + y + 3) = [(x2 + 2.x.3 + 32) – y2] : (x + y + 3)
= [(x + 3)2 – y2] : (x + y + 3) (Xuất hiện hằng đẳng thức (3))
= (x + 3 + y)(x + 3 – y) : (x + y + 3) = x + 3 – y = x – y + 3
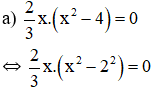
(Xuất hiện hằng đẳng thức (3))
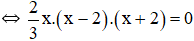
⇔ x = 0 hoặc x – 2 = 0 hoặc x + 2 = 0
+ x – 2 = 0 ⇔ x = 2
+ x + 2 = 0 ⇔ x = -2
Vậy x = 0; x = -2; x = 2
b) (x + 2)2 – (x – 2)(x + 2) = 0 (Có x + 2 là nhân tử chung)
⇔ (x + 2)[(x + 2) – (x – 2)] = 0 ⇔ (x + 2)(x + 2 – x + 2) = 0
⇔ (x + 2).4 = 0 ⇔ x + 2 = 0 ⇔ x = - 2
Vậy x = -2
a) Ta có: x2 – 2xy + y2 + 1 = (x2 – 2xy + y2) + 1 = (x – y)2 + 1.
(x – y)2 ≥ 0 với mọi x, y ∈ R
⇒ x2 – 2xy + y2 + 1 = (x – y)2 + 1 ≥ 0 + 1 = 1 > 0 với mọi x, y ∈ R (ĐPCM).
b) Ta có:
Ta có: 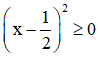
⇒ 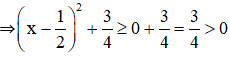
⇒ 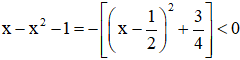
Cách 1: Thực hiện phép chia 2n2 – n + 2 cho 2n + 1 ta có:
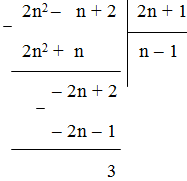
2n2 – n + 2 chia hết cho 2n + 1 ⇔ 3 ⋮ (2n + 1) hay (2n + 1) ∈ Ư(3) ⇔ 2n + 1 ∈ {±1; ±3}
+ 2n + 1 = 1 ⇔ 2n = 0 ⇔ n = 0
+ 2n + 1 = -1 ⇔ 2n = -2 ⇔ n = -1
+ 2n + 1 = 3 ⇔ 2n = 2 ⇔ n = 1
+ 2n + 1 = -3 ⇔ 2n = -4 ⇔ n = -2.
Vậy n ∈ {-2; -1; 0; 1.}
Cách 2:
Ta có:
2n2 – n + 2 chia hết cho 2n + 1
⇔ 2n + 1 ∈ Ư(3) = {±1; ± 3}.
+ 2n + 1 = 1 ⇔ 2n = 0 ⇔ n = 0
+ 2n + 1 = -1 ⇔ 2n = -2 ⇔ n = -1
+ 2n + 1 = 3 ⇔ 2n = 2 ⇔ n = 1
+ 2n + 1 = -3 ⇔ 2n = -4 ⇔ n = -2.
Vậy n ∈ {-2; -1; 0; 1.}
Chú ý: Đa thức A chia hết cho đa thức B khi phần dư của phép chia bằng 0.





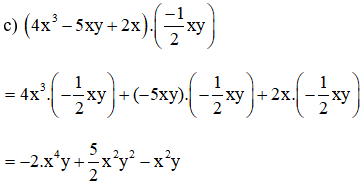
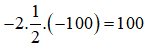
















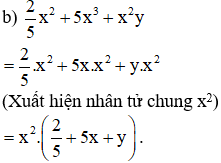
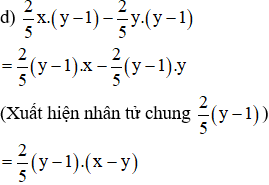
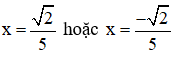

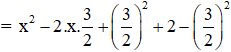
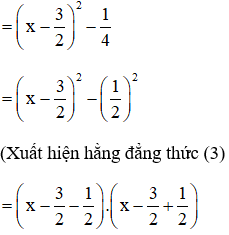
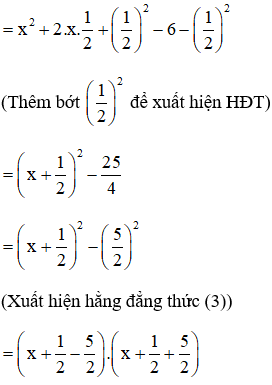








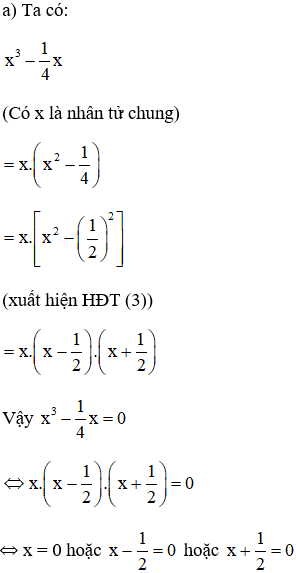
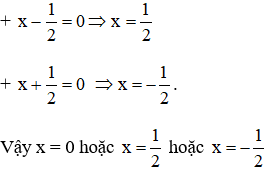
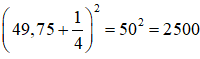
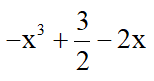
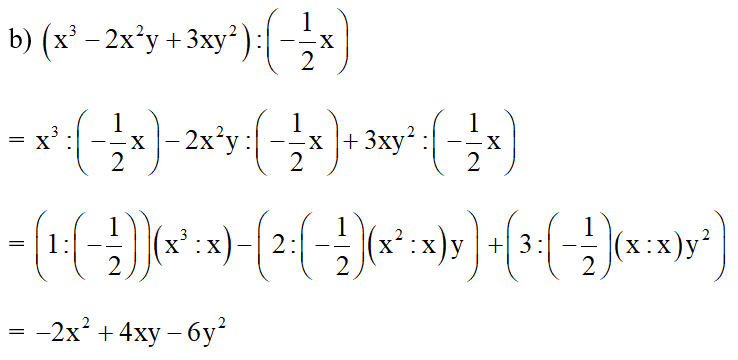


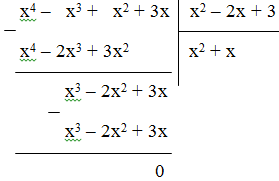

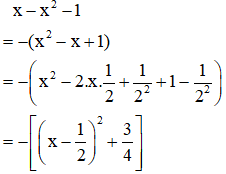
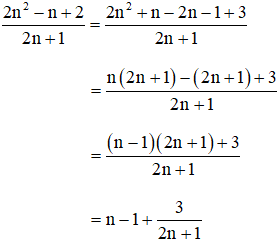
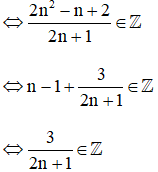


Nhận xét
Đăng nhận xét