[ĐS10] HÀM SỐ - &02. Ôn tập chương 2
Hướng dẫn giải.
a) Kết luận (B);
b) Kết luận (A);
c) Kết luận (C).
a) Hiển nhiên tập xác định D của y = ax + b là đối xứng.
Đặt f(x) = ax + b là hàm số lẻ ⇒ ∀ x ∈ D, f(x) = -f(-x) ⇔ ax + b = ax - b ⇔ b = 0.
Vậy các hàm số lẻ trong tập hợp các hàm số bậc nhất là hàm số y = ax.
b) Tương tự ta tìm được các hàm số chẵn trong các hàm số bậc hai là các hàm số có dạng y = ax2 + b.
a) Vì bề lõm của parabol quay xuống dưới nên a < 0
Lại vì –b/(2a) < 0 nên –b/2 > 0 ⇒ b < 0
Do parabol cắt Oy tại điểm có tung độ dương nên c > 0.
b) a > 0; b < 0; c > 0.
c) a > 0; b > 0 ; c = 0.
d) a < 0; b > 0; c < 0.
a) Tọa độ giao điểm là: A(0; -1), B(3; 2).
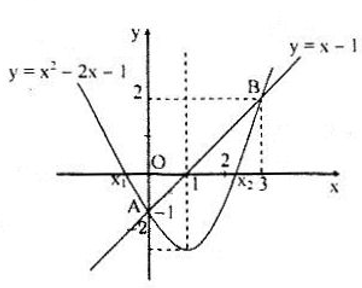
b)
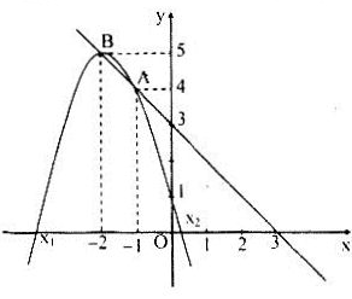
Tọa độ giao điểm (x; y) là nghiệm của hệ :
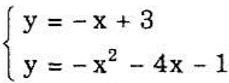
Giải ra ta đi đến có hai giao điểm: A(-l; 4), B(-2; 5).
c) Tọa độ giao điểm là: A(3 -√5; 1 - 2√5) và B(3 + √5; 1 + 2√5 ).
Đặt f(x) = ax2 + bx + c , ta có f(1) = 1, f(1/2) = ¾ và –b/(2a) = 1/2
Từ những phương trình trên ta đi đến kết quả a = 1, b = -1, c = 1
Hàm số cần tìm có dạng : y = x2 – x + 1
Bảng biến thiên :
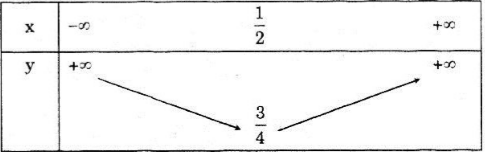
Đồ thị :
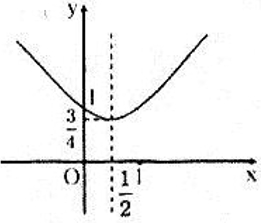
a) Đồ thị :
Bảng biến thiên :
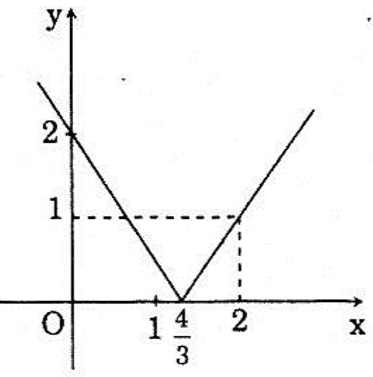
b) Đồ thị :
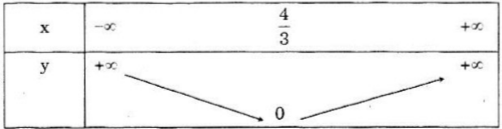
Bảng biến thiên :
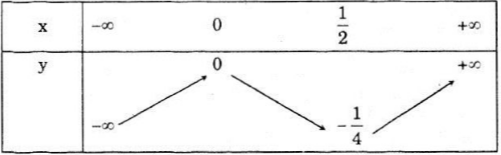
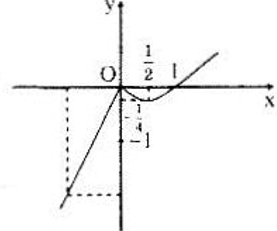
c) Đồ thị :
Bảng biến thiên :
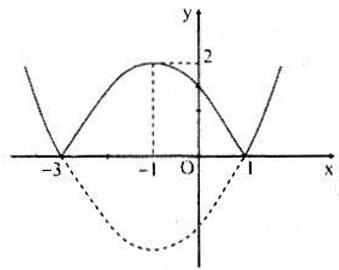
d) Ta viết lại hàm số dưới dạng :
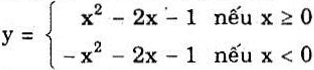
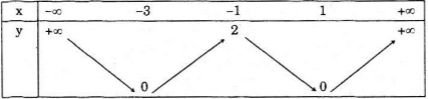
Từ đó ta có đồ thị :
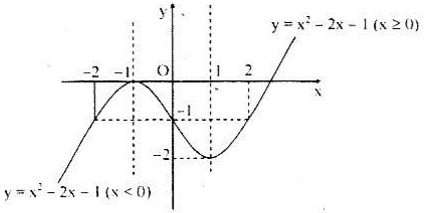
Từ đó ta có bảng biến thiên :

Nếu 2 ≤ x ≤ 6 thì S(x) = 6 + 5(x - 2) = 5x - 4.
Nếu 6 ≤ x ≤ 9 thì S(x) = 26 + 7(x - 6) = 7x - 16.
Vậy :
a) Ta cần tìm hàm số dạng y = ax2 + bx + c = f(x) thỏa f(0) = c = -7; f(10) = 4; f(20) = 5. Từ đó ta có a = 0,03 và b = 0. Hàm số cần tìm là y = 0,03x2 - 7.
b) Theo điều kiện, khi x = 100 thì y = 294 ± 1,5 nghĩa là: y ∈ [292,5; 295,5],
Ta thấy f(l00) = 293 thỏa mãn điều kiện đó.


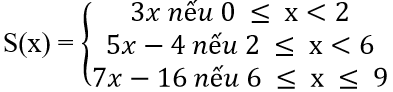


Nhận xét
Đăng nhận xét