[ĐS10] HÀM SỐ - &01. Hàm số bậc 1, bậc 2 (phần 2)
Hướng dẫn giải.
a) Do phương trình x2 - x + 1 = 0 vô nghiệm nên x2 - x + 1 ≠ 0, ∀ x ∈ R Từ đây ta suy ra tập xác định của hàm số là R.
b) Ta có phương trình: x2 - 3x + 2 = 0 có tập nghiệm là {1; 2}. Từ đây ta suy ra: x2 - 3x + 2 ≠ 0 ⇔ x ∈ R \ {1; 2}. Vậy tập xác định của hàm số là R \ {1; 2}.
c) Biểu thức √(x-1)/(x – 2) có nghĩa khi và chỉ khi x – 1 ≥ 0 và x – 2 ≠ 0 hay x ≥ 1 và x ≠ 2. Vậy tập xác định của hàm số là : [1; 2) ∪ (2; +∞).
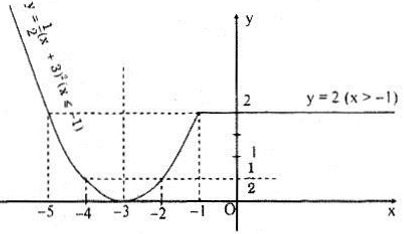
d) Biểu thức có nghĩa khi và chỉ khi x + 2 ≠ 0 và x + 1 > 0 ⇔ x ≠ 2 và x > -1 ⇔ x > -1
Vậy tập xác định của hàm số là ( - 1; +∞)
f(2000) = 3,48; f((2001) = 3,72);
f(2002) = 3,24; f(2003) = 3,82;
f(2004) = 4,05; f(2005) = 5,20.
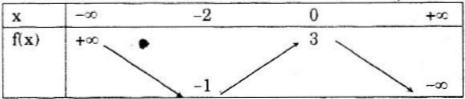
a)Ta có :
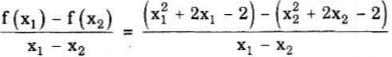
= x2 + x2 + 2 = x2 + 1 + x2 + 1 < 0 (vì x2, x2 ∈ (-∞; -1) nên x2 < -1 và x2 < -1
Hay x2 + 1 < 0 và x2 + 1 < 0)
Với x2, x2 ∈ (-1; + ∞ ) tức là x2 > -1 và x2 < -1
Hay x2 + 1 < 0 và x2 + 1 < 0
Suy ra x2 + x2 + 2 < 0. Nên hàm số đồng biến trên (-1 ; + ∞ )
b) Ta có :
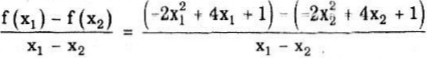
= -2(x2 + x2 – 2)
Suy ra hàm số đồng biến trên khoảng (- ∞ ; 1) vì x2, x2 ∈ (- ∞ ; 1) tức là x2 < 1 và x2 < 1 hay x2 – 1 < 0 và x2 – 1 < 0 hay x2 + x2 – 2 < 0). Tương tự ta suy ra được hàm số nghịch biến trên khoảng (1; + ∞ )
c) Ta có :
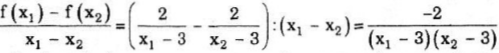
Tương tự như ở phần b) suy ra được hàm số nghịch biến trên mỗi khoảng (- ∞; 3) và (3; + ∞ )
a) Hàm số y = f(x) = x4 - 3x2 + 1 có tập xác định D là R, do đó ∀ x ∈ D thì -x ∈ D, hơn nữa f(-x) = (-x)4 - 3(-x)2 + 1 = x4 - 3x2 + 1 = f(x), nên y = f(x) là hàm số chẵn.
b) Hàm số y = g(x) = -2x3 + x có tập xác định D là R, do đó ∀ x ∈ D thì -x ∈ D, hơn nữa g(-x) = -2(-x)3 + (-x) = 2x3 - x = -g(x), nên y = g(x) là hàm số lẻ.
c) Hàm số y = h(x) =|x + 2|- |x - 2 | có tập xác định D là R, do đó ∀ x ∈ D thì –x ∈ D, hơn nữa h(-x) = | -x + 2| -|-x – 2|= |x - 2| - |x + 2|= -(|x + 2| - |x - 2 |) = -h{x)
Vì vậy y = h(x) là hàm số lẻ.
d) Chứng minh tương tự ta có y = |2x + 1| + |2x — 1| là hàm số chẵn.
a) Tịnh tiến (d) lên trên 3 đơn vị, ta được đồ thị của hàm số: y = f(x) + 3 hay y = 0,5x + 3.
b) Tịnh tiến (d) xuống dưới 1 đơn vị, ta được đồ thị của hàm số: y = f(x) - 1 hay y = 0,5x - 1.
c) Tịnh tiến (d) sang phải 2 đơn vị, ta được đồ thị của hàm số:
y = f(x - 2) = 0,5(x - 2) hay y = 0,5x - 1.
d) Tịnh tiến (d) sang trái 6 đơn vị, ta được đồ thị của hàm số: y = f(x + 6) = 0,5(x + 6) hay y = 0,5x + 3.
Nhận xét: đồ thị nhận được ở a) và đồ thị nhận được ở d) là một.
- Đồ thị nhận được ở b) và đồ thị nhận được ở c) cũng là một.
a)
- (d) và (G) có điểm chung khi a ∈ D.
- (d) và (G) không có điểm chung khi a ∉ D.
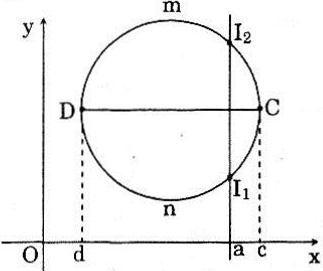
Hình vẽ bên minh họa cho trường hợp D = (d; c). Trường hợp a = a1 ∈ D, ta có (d1) có giao điểm với (G) tại I.
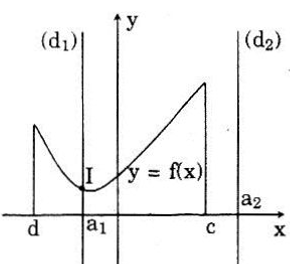
Trường hợp a = a2 ∉ D thì (d2) và (G) không có giao điểm.
b) (d) và (G) có không quá một điểm chung, vì nếu trái lại, gọi M1 và M2 là hai điểm chung phân biệt thì ứng với a có tới hai giá trị của hàm số là các tung độ của điểm M1, M2. Trái với định nghĩa của hàm số.
c) Đường tròn trong mặt phẳng tọa độ không là đồ thị của hàm số vì có đường thẳng song song với Oy cắt nó tại hai điểm phân biệt.
Chú ý: Đường tròn có thể coi là sự hợp bởi hai đồ thị hàm số. Ở hình bên ta có thể xem đường tròn là sự hợp bởi hai đồ thị hàm số nên đồ thị (G1) là cung DmC và đồ thị (G2) là cung DnC.
a) Biểu thức (3x + 1)/(x2 – 9) có nghĩa khi và chỉ khi x2 – 9 ≠ 0 ⇔ x ≠ 3 và x ≠ -3
=> tập xác định của hàm số đã cho là R\ {3; -3}
b) Biểu thức x/(1 – x2) - √(-x) có nghĩa ⇔ 1 – x2 ≠ 0 và –x ≥ 0
⇔ x ≠ 1 và x ≠ -1 và x ≤ 0 ⇔ {x ≤ 0 và x ≠ -1} => Tập xác định của hàm số là (- ∞ ; 0]\{-1}
c) Biểu thức (x - 3√(2 - x))/ √(2 + x) có nghĩa ⇔ {2 – x ≥ 0 và x + 2 > 0 } => -2 ≤ x ≤ 2
=> Tập xác định của hàm số là : nửa khoảng (-2; 2]
d)Tập xác định của hàm số là : [1; 4) ∪ (2; 3) ∪ (3;4].
a) Tập xác định của hàm số là : [-1; + ∞ )
b) f(-1) = 6; f(0,5) = 3; f(√2/2) = 4 - √2; f(1) = 0; f(2) = √3
Điểm D thuộc đồ thị hàm số vì f(5) = 25 + √2
a) Hàm số y = 1/(x – 2) nghịc biến trên mỗi khoảng (- ∞; 2) và (2; + ∞ )
b) Hàm số y = x2 – 5x + 6 nghịch biến trên khoảng (- ∞; 3) và đồng biến trên khoảng (3; + ∞)
c) Với mọi x1, x2 ∈ (- ∞; + ∞), ta có x1 < x2 => x12005 < x22005
=> x12005 + 1 < x22005 + 1 hay f(x1) < f(x2) (y = f(x) = x2005 + 1). Từ đấy ta có, hàm số đã cho đồng biến trên (- ∞; + ∞)
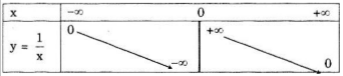
a)Bảng biến thiên :
b)Với mọi x1, x2 ∈ (0; + ∞ ) ta có 0 < x1 < x2 => 1/x1 > 1/x2 , suy ra hàm số nghịch biến trên khoảng (0; + ∞ ).
Với mọi x1, x2 ∈ (- ∞; 0), ta có x1 < x2 < 0 => -x1 > -x2 > 0 => 1/(-x1) < 1.(-x2) => 1/x1 > 1/x2, suy ra hàm số nghịch biến trên khoảng (- ∞; 0)
Chú ý : Ta cũng có thể làm như sau : Trên mỗi khoảng (- ∞; 0) và (0; + ∞) , x1 và x2 luôn cùng dấu . Do đó :
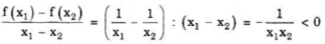
a) Gọi f(x) = 2x. Khi đó 2x - 3 = fix) - 3. Do đó, muôn có (d') ta tịnh tiến (d) xuống 3 đơn vị.
b) Cũng có thể viết 2x - 3 = 2(x – 3/2) = f(x – 3/2). Do đó, muốn có (d'), ta tịnh tiến (d) sang phải 3/2 đơn vị.
a) Đặt f()x) = -2/x , khi tịnh tiến đồ thị (H) lên trên một đơn vị, ta được đồ thị hàm số y = f(x) + 1 = -2/x + 1 = (x – 2)/x. Gọi đồ thị mới này là (H1).
b) Khi tịnh tiến (H) sang trái 3 đơn vị, ta được đồ thị của hàm số y = f(x + 3) = -2/(x + 3)
c) Đồ thị nhận được chính là tịnh tiến (H1) sang trái 3 đơn vị. Do đó, ta được đồ thị của hàm số y= f(x + 3) + 1 = -2/(x + 3) + 1 = (x + 1)/(x + 3)
a) y = (1/√2).x + 1 Và e) y = (1/√2).x – 1
c) y = (2/√2).x + 2 Và d) y = √2.x – 2
b) y = (-1/√2).x + 3 Và g) y = -[(√2/2).x – 1]
Hướng dẫn giải.
a) Tập xác định của hàm số là đoạn [-2; 3]
b)
• Trên khoảng (-2; -1) hàm số đồng biến;
• Trên khoảng (-1; 1) hàm số nghịch biến;
• Trên khoảng (1; 3) hàm số đồng biến.
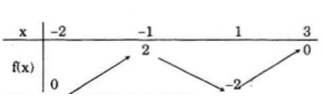
Đồ thị được cho ở hình dưới đây :
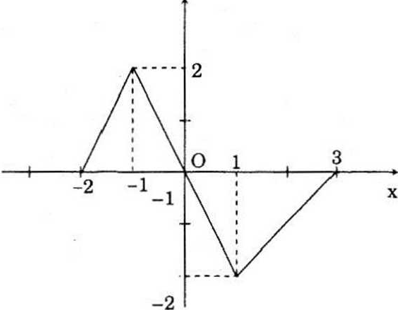
a)Ta có đồ thị hàm số f1 và f2 ở hình bên
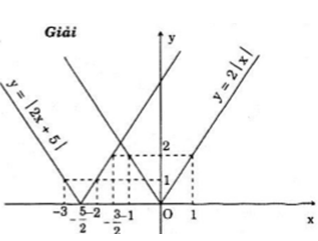
b) Phép tịnh tiến sang trái 5/2 đơn vị biến đồ thị hàm số y = 2|x| thành đồ thị hàm số y = |2x + 5|. Thật vậy, ta có : f1(x + 5/2) = 2|x + 5/2| = |2(x + 5/2)| = f2(x)
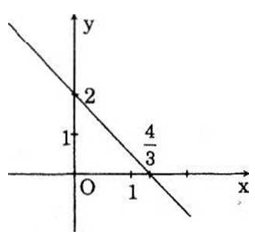
a) Hàm số đã cho là hàm số bậc nhất và có dạng y = -l,5x + b. Vì đồ thị đi qua (-2; 5) nên ta có: 5 = -1,5(-2) + b 5 = + 3 + b => b = 2 . Hàm số cần tìm là : y = (-3/2).x + 2
b) Đồ thị của hàm số y = (-3/2).x + 2 như hình vẽ :
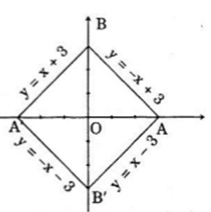
Do tính chất O là tâm đối xứng của hình vuông nên đỉnh đối diện với A là A' có tọa độ (-3; 0). Do hai đường chéo của hình vuông là vuông góc với nhau nên hai đỉnh còn lại thuộc Oy và dễ dàng có: B(0; 3), B'(0; -3) là hai đỉnh còn lại, từ đó suy ra 4 hàm số cần tìm là:
y = x + 3; y = -x + 3; y = x - 3; y = -x - 3.
a) Khi tịnh tiến (G) lên trên 3 đơn vị ta được đồ thị hàm số: y = 2 |x| +3
b) Khi tịnh tiến (G) sang trái 1 đơn vi, ta được đồ thị hàm số: y = 2 |x + 1|
c) Trước hết tịnh tiến (G) sang phải 2 đơn vị ta được đồ thị của hàm số y = 2|x - 2 |, gọi đồ thị của hàm số này là (G'). Tịnh tiến (G') xuống dưới 1 đơn vị, ta được đồ thị hàm số y = 2|x - 2| -1
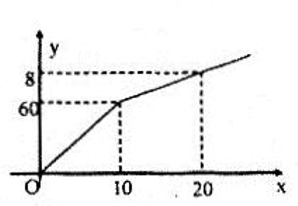
a) Khi 0 ≤ x ≤ 10, tức là quãng đường đi năm trong l0km đầu tiên, số tiền phải trả là f(x) = 6x (nghìn đồng). Khi x > 10, tức là quãng đường đi trên l0km thì số tiền phải trả gồm hai khoản: l0km đầu phải trả với 6 nghìn đồng cho một kilômét và (x - 10) km tiếp theo phải trả với giá 2,5 nghìn đồng cho một kilomet. Do đó f(x) = 60 + 2,5(x – 10) hay f(x) = 2,5x + 35. Vậy hàm số phải tìm là :
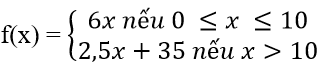
b)Từ công thức xác định f(x) ta có : f(8) = 48; f(10) = 60; f(18) = 80
c)Đồ thị hình bên :
Bảng biến thiên :

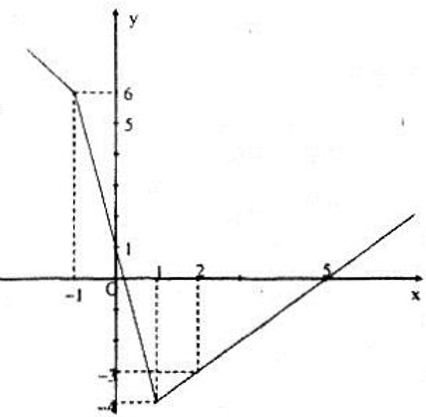
a)
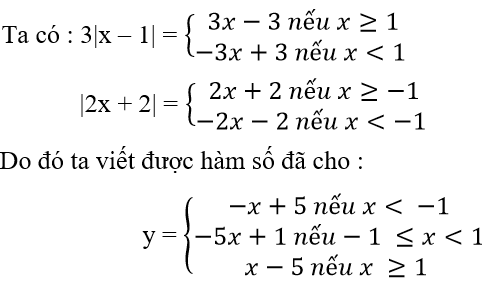
b) Đồ thị là hình vẽ dưới đây
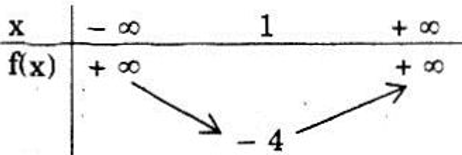
Bảng biến thiên :
a)
– Đỉnh của parabol là điểm có tọa độ (0; -3);
- Parabol có trục đối xứng là trục Oy;
- Parabol hướng bề lõm xuống dưới.
b)
– Đỉnh của parabol là điểm có tọa độ (3; 0);
- Parabol có trục đối xứng là đường thẳng x = 3;
- Parabol hướng bề lõm lên trên.
c)
- Đỉnh của parabol là điểm có tọa độ (0; 1);
- Parabol có trục đối xứng là đường thẳng x = 0;
- Parabol hướng bề lõm về phía trên.
d)
- Đỉnh của parabol là điểm có tọa độ (-1; 0);
- Parabol có trục đối xứng là đường thẳng x = -1;
- Parabol hướng bề lõm về xuống dưới.
a) Từ giả thiết ta có ngay 3 = 4a + c (1)
Do hàm số nhận giá trị nhỏ nhất là -1 nên a > 0 và khi đó y = ax2 + c > c => giá trị nhỏ nhất đạt được là c khi x = 0.
Vì vậy c = -1, thay c = -1 vào (1) ta có: a = 1.
b) Do đỉnh của (P) là (0; 3) nên ta có: 3 = c. Khi đó hoành độ giao điểm của (P) với Ox là nghiệm của phương trình ax2 + 3 = 0. Do giả thiết phương trình này có nghiệm x= -2 nên ta có: 4a + 3 = 0 ⇔ a = -3/4
a) Vì Parabol có đỉnh là (-3; 0) nên a(-3 - m)2 = 0 , m = -3 Parabol cắt Oy tại M(0; -5)
Nên ta có: -5 = a.(0 + 3)2 => a = -5/9. Vậy a = -5/9. M = -3
b) Từ giả thiết ta suy ra phương trình y = a(x - m)2 nhận 2 cặp số y = 4, x = -1 và y = 4, x = 3 là nghiệm.
Từ đó ta thay vào phương trình tìm được: a = m = 1. Vậy a = m = 1 thỏa yêu cầu bài toán.
a) Ta viết lại hàm số dưới dạng y = 1(x - 4)2 - 4. Từ đấy ta thấy đồ thị hàm số này có được bằng cách tịnh tiến parabol y = x2 sang phải 4 đơn vị, rồi xuống dưới 4 đơn vị.
b) Ta viết lại hàm số dưới dạng y = -3(x + 2)2 + 21. Đồ thị của hàm số này có được bằng cách tịnh tiến đồ thị hàm số y = -3x2 sang trái hai đơn vị sau đó tịnh tiến tiếp đồ thị hàm số mới thu được lên trên 21 đơn vị.
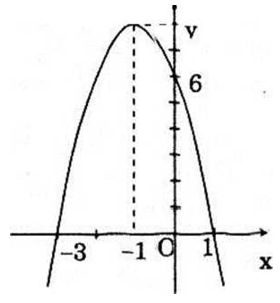
a) Đỉnh D(-l; 8), trục đối xứng có phương trình x = -1.
b) Đồ thị ở hình bên
c) y ≥ 0 ⇔ -3 ≤ x ≤ 1
d) Vậy S = {x ∈ R|-3 ≤ x ≤ 1} = [-3; 1] là tập hợp cần tìm.
a)
- Hàm số y = -x2 + 2x + 3
Đồ thị hàm số có trục đôi xứng là x = 1;
Tọa độ đỉnh (1; 4)
Đồ thị giao với Oy tại C(0; 3)
Đồ thị giao với Ox tại hai điểm A(-1; 0); B(3; 0)
Parabol quay bề lõm xuống dưới
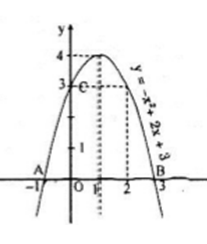
Từ đồ thị vừa vẽ ta có :
b) y > 0 ⇔ -1 < x < 3
c) y < 0 ⇔ x < -1 hoặc x > 3
Hàm số y = (1/2)x2 + x – 4
- Đồ thị có trục đối xứng : x = -1;
- Tọa độ đỉnh (-1; -9/2)
- Đồ thị giao với Oy tại (0; -4)
- Đồ thị giao với Ox tại A(-4; 0) ; B(2; 0)
- Đồ thị quay bề lõm về phía trên
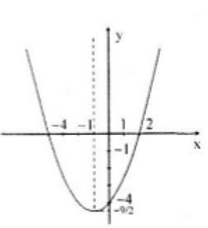
Từ đồ thị vừa vẽ ta có :
b) y > 0 ⇔ x > 2 hoặc x < -4
c) y < 0 ⇔ -4 < x < 2
| Hàm số | Hàm số có giá trị lớn nhất/ nhỏ nhất khi x = ? | Giá trị lớn nhất | Giá trị nhỏ nhất |
| y = 3x2 - 6x + 7 | x = 1 | y = 4 | |
| y = -5x2 - 5x + 3 | x = -1/2 | y = 17/4 | |
| y = x2 - 6x + 9 | x = 3 | y = 0 | |
| y = -x2 + 4x - 1 | x = 1/2 | 0 |
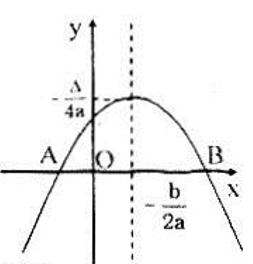
a)Vì (P) nằm hoàn toàn ở phía trên trục hoành nên a > 0 hơn nữa do (P) ở phía trên trục hoành nên (P) ∪ Ox = ∅ ⇒ ax2 + bx + c = 0 vô nghiệm ⇔ Δ < 0
b)Tương tự ta cũng có :
a < 0 và Δ < 0
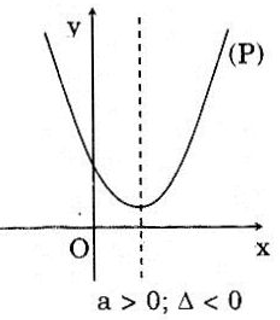
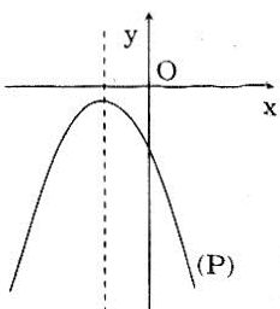
c)(P) phải có hình dạng ở hình vẽ bên, do đó phương trình
ax2 + bx + c = 0 có hai nghiệm phân biệt ⇔ Δ > 0
Mặt khác theo giả thiết thì - Δ /(4a) > 0 ⇔ 1/a < 0 ⇔ a < 0
Vậy a < 0, Δ > 0
a) Trước hết vẽ parabol y = x2 + √2x và parabol y = -(x2 + √2x) (chú ý là hai parabol này đối xứng với nhau qua Ox), sau đó chỉ việc xoá đi phần phía dưới Ox của cả hai parabol ấy, ta có đồ thị hàm số y = |x2 + √2x|
Từ đồ thị ta có bảng biến thiên:
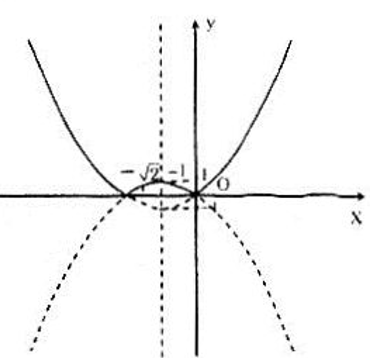
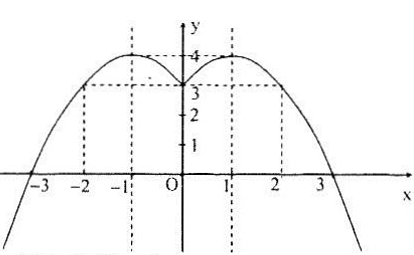
b) Ta nhận thấy hàm số y = -x2 + 2 |x| + 3 là hàm số chẵn, bởi vậy ta chỉ cần vẽ đồ thị ở bên phải Oy sau đó lấy tiếp phần đồ thị đối xứng với phần vừa vẽ qua Oy.
Trước hết ta vẽ đồ thị hàm số y = -x2 + 2x + 3 bên phải Oy, tiếp theo lấy đối xứng với phần này qua Oy ta được đồ thị hàm số đã cho.
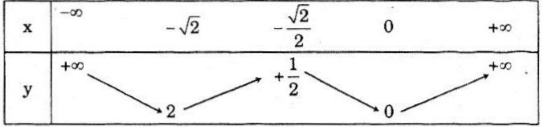
Từ đồ thị ta có bảng biến thiên như sau:
c) Ta viết hàm số lại dưới dạng:

Đồ thị dưới đây:
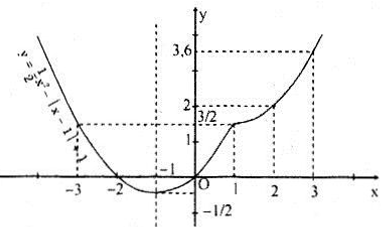
Từ đồ thị ta có bảng biến thiên
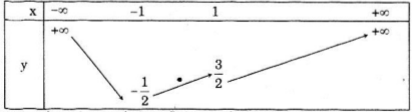
a)
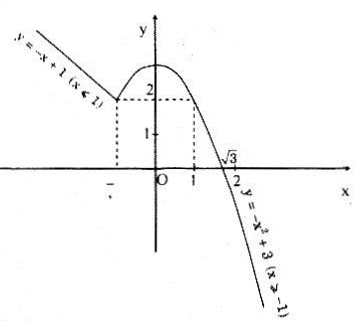
b)
a) Giả sử h = f(t) = at2 + bt + c. Ta cần tìm a, b, c.
Theo giả thiết quả bóng được đá lên từ độ cao l,2m, nghĩa là f(0) = 1,2 ⇒ c = 1,2. Sau đó 1 giây, nó đạt độ cao 8,5m nên f(1) = a + b + 1,2 = 8,5. 2 giây sau khi đá quả bóng lên, quả bóng ớ độ cao 6m, nghĩa là f(x) = 4a + 2b + 1,2 = 6 từ đó ta có hệ phương trình bậc nhất: {a+b=7,3 và 2a+b=2,4}
Giải hệ này ta có a = -4,9, b = 12,2. Vậy hàm số cần tìm là: f(t) = 4,9t2 + 12,2t + 1,2
b) Giải phương trình -4,9t + 12,2t + 1,2 = 0, ta được nghiệm gần đúng là -0,09 và 2,58. Vậy quá bóng chạm đất sau 2,58 giây.
c) Độ cao cực đại xấp xỉ bằng 8,794m.
a) Hàm số cần tìm có dạng f(x) = ax2 + bx + c, thỏa mãn:
f(0) = c = 0, f(10) = 100a + 10b = 43;
f(162) = 1622a + 162b = 0 hay 162a + b = 0
Từ đó ta tìm được a = -43/1520; b = 3483/760; c = 0, ta suy ra hàm số cần tìm
b) h = f(162/2) = f(81) ≈ 186 (m)































Nhận xét
Đăng nhận xét