[ĐS & GT] TỔ HỢP - &03. Tổ hợp và Xác suất
Hướng dẫn giải.
a) Không gian mẫu Ω = {1, 2, 3,...50}
b) Kết quả thuận lợi cho A là :

a) A là biến cố “số được chọn là số nguyên tố”. Ta có ΩA = {2, 3, 5, 7}
Xác suất để số được chọn là số nguyên tố là:
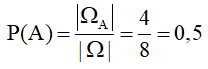
b) Gọi B là biến cố “số được chọn chia hết cho 3”
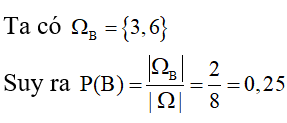
a) Gọi A là biến cố “Hường được chọn”
Ta có P(A) = 1/30
b) Gọi B là biến cố “Hường không được chọn”
Ta có P(B) = 29/30
c) Gọi C là biến cố “Bạn có số thứ tự nhỏ hơn 12 được chọn”
Ta có P(C) = 11/30
a) Ω = {(a, b)|a, b ∈ N*, 1 ≤ a ≤ 6,1 ≤ b ≤ 6}
Không gian mẫu có 36 phần tử.
b) ΩA = {(6; 1),(5; 1); (5; 2),(4;2),(4;3),(3;1),(3;2),(3;3),(3;4),(2;1),(2;2),(2;3),(2;4),(2;5),(1;1),(1;2),(1;3),(1;4),(1;5),(1;6) }
Tập ΩA có 21 phần tử. Vậy P(A) = 21/36 = 7/12
c) ΩB = {(6;1),(6;2),(6;3),(6;4),(6;5),(6;6),(1;6),(2;6),(3;6),(4;6),(5;6)}
Tập ΩB có 11 phần tử. Vậy P(B) = 11/36
ΩC = {(6;1),(6;2),(6;3),(6;4),(6;5),(1;6),(2;6),(3;6),(4;6),(5;6)}
Tập ΩC có 10 phần tử. Vậy P(C) = 10/36 = 5/18
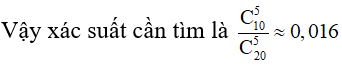
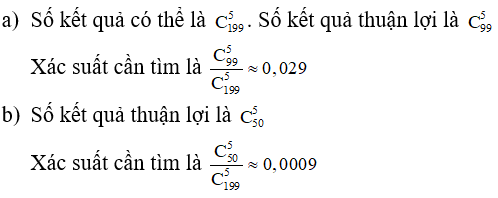
Vậy xác suất cần tìm là 8/36 = 2/9 .
Hướng dẫn giải.
a) Gọi Ai là biến cố “đồng xu thứ i sấp”, (i = 1,2,3). Ta có P(Ai) = 1/2 . Các biến cố Ai độc lập. Theo quy tắc nhân xác suất ta có :
P(A1A2A3) = P(A1).P(A2).P(A3) = 1/8

a)

b)

Gọi B1 là biến cố “ đồng xu B sấp”, B2 là biến cố “đồng xu B ngửa”
Theo bài ra ta có: P(A1) = P(A2) = 0,5, P(B1) = 0,75.P(B2) = 0,25
a) A2B2 là biến cố “cả 2 đồng xu đều ngửa”. theo quy tắc nhân xác suất ta có:
P(A2B2) = 0,5.0,25 = 0,125
b) Gọi H1 là biến cố “khi gieo lần đầu cả 2 đồng xu đều ngửa”, H2 là biến cố “khi gieo lần hai cả 2 đồng xu đều ngửa”. Khi đó H1H2 là biến cố “khi gieo hai lần cả hai đồng xu đều ngửa”.
Từ a) ta có P(H1) = P(H2) = 0,5.0,25 = 0,125
Áp dụng quy tắc nhân xác suất ta có P(H1H2) = P(H1).P(H2) = 0,125.0,125 = 1/64
Khi đó A1A2...A10 là biến cố “học sinh đó trả lời không đúng cả 10 câu”
Từ giả thiết ta có P(Ai) = 0,8 .
Áp dụng quy tắc nhân xác suất ta có
P(A1A2...A10) = P(A1).P(A2)...P(A10) = (0,8)10 ≈ 0,1074
Hướng dẫn giải.
Gọi H là biến cố “trong 2 thẻ rút ra có ít nhất 1 thẻ đánh số 12”. Khi đó biến cố đối của H là :

a) Vì P(AB)=0,2 ≠ 0 nên 2 biến cố A và B không xung khắc
b) Ta có P(A).P(B) = 0,12 ≠ P(AB) = 0,2 nên hai biến cố A và B không độc lập với nhau.

Vậy n nhỏ nhất là 6 hay An phải chơi tối thiểu 6 trận.
Khi đó P(B) = 5/36
Kết quả của T là bộ ba số (x,y,z) trong đó x,y,z tương ứng là kết quả của việc gieo súc sắc thứ nhất, thứ hai và thứ ba. Không gian mẫu T có 6.6.6=216 phần tử. Gọi A là biến cố “tổng số chấm trên mặt xuất hiện của ba con súc sắc bằng 9”. Ta có tập hợp các kết quả thuận lợi cho A là: ΩA = {(x;y;z)|x + y + z = 9,x, y, z ∈ N*, 1 ≤x,y,z ≤ 6}
Nhận xét: 9 = 1 + 2 + 6 = 1 + 3 + 5 = 2 + 3 + 4 = 1 + 4 + 4 = 2 + 2 + 5 = 3 + 3 + 3
Tập {1,2,6} cho ta 6 phần tử của ΩA là (1,2,6); (1,6,2); (2,1,6); (2,6,1); (6,1,2); (6,2,1).
Tương tự tập {1,3,5},{2,3,4} mỗi tập cho ta 6 phần tử của ΩA .
Mỗi tập {1,4,4},{2,2,5} cho ta 3 phần tử của ΩA
Tập {3,3,3} cho ta 1 phần tử của ΩA
Vậy |ΩA| = 6 + 6 + 6 + 3 + 3 + 1 = 25
Suy ra P(A) = 25/216
- Giá trị của X là một số thuộc tập hợp {1,2,…,100} (vì số người trong mỗi gia đình ở VN không thể vượt quá 100).
- Giá trị của X là ngẫu nhiên (vì nó phụ thuộc vào bạn học sinh mà ta chọn ngẫu nhiên)
Không gian mẫu gồm 8 phần tử sau: {TTT, TTG, TGT, TGG, GTT, GTG, GGT, GGG}
(trong đó T:trai, G:gái)
Như vậy không gian mẫu gồm 8 kết quả đồng khả năng.
Gọi Ak là biến cố “gia đình có k con trai” (k = 0,1,2,3)
P(X = 0) = P(Ao) = 1/8 (vì chỉ có 1 kết quả thuận lợi cho Ao là GGG)
P(X = 1) = P(A1) = 3/8 (vì có 3 kết quả thuận lợi cho A1 là TGG, GTG,GGT)
P(X = 2) = P(A2) = 3/8 (vì có 3 kết quả thuận lợi cho A2 là GTT,TGT,TTG)
P(X = 3) = P(A3) = 1/8 (vì chỉ có 1 kết quả thuận lợi cho A3 là TTT)
Vậy bảng phân bố xác suất của X là:
a) Gọi A là biến cố “phải tăng cường them bác sĩ trực”. từ điều kiện của bài ra, ta có :
P(A) = P(X > 2) = P(X = 3) + P(X = 4) + P(X = 5) = 0,2 + 0,1 + 0,05 = 0,35
b) P(X > 0)=1 - P(X = 0) = 1 - 0,15 = 0,85.
=0,15 + 0,1 + 0,1 = 0,35
Bảng phân bố xác suất của X là :

Bảng phân bố xác suất của X là:

Bảng phân bố xác suất của X là :

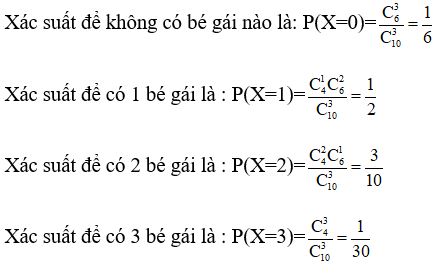
Vậy bảng phân bố xác suất của X là :

a) Xác suất để số đơn hàng đặt thuộc đoạn [1;4] là:
P(1 ≤ X ≤ 4) = P(X = 1) + P(X = 2) + P(X = 3) + P(X = 4) = 0,2 + 0,4 + 0,1 + 0,1 = 0,8
b) Ta có P(X ≥ 4) = P(X = 4) + P(X = 5) = 0,1 + 0,1 = 0,2
c) Số đơn đặt hàng trung bình đến công ty trong 1 ngày là kì vọng của X.
E(X)= 0.0,1 + 1.0,2 + 2.0,4 + 3.0,1 + 4.0,1 + 5.0,1 = 2,2
a) Ta có : P(2 < X < 7) = P(X = 3) +P(X = 4) +P(X = 5) +P(X = 6)
=0,14 + 0,18 + 0,25 + 0,15 = 0,72.
b) P(X > 5)= P(X = 6) +P(X = 7) +P(X = 8) +P(X = 9)
=0,15 + 0,07 + 0,04 + 0,01 = 0,27
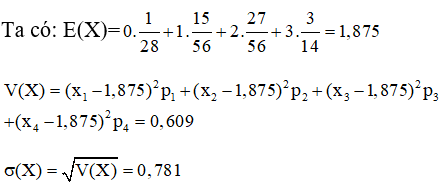
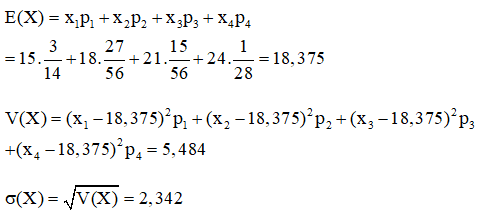

























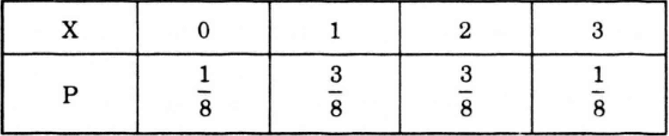


Nhận xét
Đăng nhận xét