[ĐS & GT] TỔ HỢP - &01. Tổ hợp và phép đếm

 

Hướng dẫn giải.

Bài 1. Theo quy tắc cộng ta có 5 + 4 = 9 cách chọn áo sơ mi.

Bài 2. Chữ số hàng chục có thể chọn trong các chữ số 2,4,6,8 do đó có 4 cách chọn. Chữ số hàng đơn vị có thể chọn trong các chữ số 0,2,4,6,8 do đó có 5 cách chọn. Vậy theo quy tắc nhân ta có 4.5 = 20 số có hai chữ số mà hai chữ số của nó đều chẵn.

Bài 3.

a) Theo quy tắc cộng, nhà trường có 280 + 325 = 605 cách chọn

b) Theo quy tắc nhân, nhà trường có 280.325 = 91000 cách chọn

Bài 4.

a) Số có 4 chữ số thỏa yêu cầu có dạng

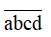
a có 4 cách chọn, b có 4 cách chọn, c có 4 cách chọn, d có 4 cách chọn.

Vậy theo quy tắc nhân có 4.4.4.4 = 256 cách chọn.

b) Số thoả yêu cầu có dạng

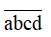
a có 4 cách chọn, b có 3 cách chọn, c có 2 cách chọn, d có 1 cách chọn

Vậy theo quy tắc nhân có 4.3.2.1 = 24 cách chọn.

Hướng dẫn giải.

Bài 5. Có 5! =120 khả năng.

Bài 6. Có A38 = 8.7.6 = 336 kết quả.

Bài 7.

a) Giả sử P = {A1, A2,...An} . Với mỗi tập con {Ai, Aj}(i ≠ j) ta tạo được đoạn thẳng AiAj và ngược lại mỗi đoạn thẳng với hai đầu mút là hai điểm Ai, Aj tương ứng với tập con {Ai, Aj} .

Thứ tự hai đầu mút không quan trọng:

đoạn thẳng AiAj và AjAi chỉ là một đoạn thẳng.

Vậy số đoạn thẳng mà hai đầu mút thuộc P là số tổ hợp chập 2 của n phần tử, tức là bằng

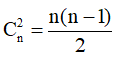
b)

Bài 8.

a) Số cách chọn 3 người mà không có sự phân biệt về chức vụ trong ban thường vụ bằng số tổ hợp chập 3 của 7 phần tử và bằng C37 = 35 cách chọn.

b) Số cách chọn 3 người với các chức vụ : Bí thư, phó bí thư, ủy viên bằng số chỉnh hợp chập 3 của 7 phần tử và bằng A37 = 210 cách chọn.

Bài 9. Bài thi có 410 = 1048576 phương án trả lời.

Bài 10. Một số tự nhiên có 4 chữ số chia hết cho 5 có dạng:

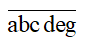
Với a có 9 cách chọn, g có 2 cách chọn và b,c,d,e mỗi số có 10 cách chọn. Vậy theo quy tắc nhân có 9.104.2 = 180000 số.

Bài 11. Có 4 phương án đi qua các tỉnh A đến G là:

a) A → B → D → E → G

b) A → B → D → F → G

c) A → C → D → E → G

d) A → C → D → F → G

Theo quy tắc nhân ta có:

Phương án a) có 2.3.2.5 = 60 cách đi

Phương án b) có 2.3.2.2 = 24 cách đi

Phương án c) có 3.4.2.5 = 120 cách đi

Phương án d) có 3.4.2.2 = 48 cách đi

Vậy theo quy tắc cộng có 60 + 24 + 120 + 48 = 252 cách đi từ A đến G.

Bài 12. Mỗi cách đóng-mở 6 công tắc của mạng điện được gọi là một trạng thái của mạng điện. Theo quy tắc nhân, mạng điện có 26 = 64 trạng thái. Trước hết ta tìm xem có bao nhiêu trạng thái không đóng mạch (không có dòng điện đi qua). Mạch gồm 2 nhánh A → B và C → D .
Trạng thái không thong mạch xảy ra khi và chỉ khi cả hai nhánh A → B và C → D đều không thông mạch. Dễ thấy nhánh A → B có 8 trạng thái trong đó có duy nhất 1 trạng thái thông mạch còn 7 trạng thái còn lại đều không thong mạch. Tương tự ở nhánh C → D có 7 trạng thái không thong mạch. Theo quy tắc nhân ta có 7.7 = 49 trạng thái mà cả A → B và C → D đều không thong mạch. Vậy mạng điện có 64 - 49 = 15 trạng thái thong mạch từ P đến Q.

Bài 13.

a) Số cách chọn ra 4 người điểm cao nhất trong 15 người tham dự là số tổ hợp chập 4 của 15 phần tử. Vậy có C415 = 1365 kết quả.

b) Số cách chọn ra 3 giải nhất, nhì, ba là số chỉnh hợp chập 3 của 15 phần tử. vậy có A315 = 2730 kết quả.

Bài 14.

a) Có A4100 = 94109400 kết quả có thể.

b) Nếu giải nhất đã xác định thì 3 giải nhì,ba,tư rơi vào 99 người còn lại. Vậy có A399 = 941094 kết quả có thể.

c) Người giữ vé số 47 có 4 khả năng trúng 1 trong 4 giải. Sau khi xác định giải của người này thì 3 giải còn lại rơi vào 99 người không giữ vé số 47. Vậy theo quy tắc nhân có 4.A399 = 3764376 kết quả có thể.

Bài 15. Số cách chọn 5 em trong 10 em là C510 . Số cách chọn 5 em toàn nam là C58 . Do đó số cách chọn có ít nhất 1 nữ là C510 - C58 = 196.

Bài 16. Số cách chọn 5 em toàn nam là C57 . Số cách chọn 4 nam và 1 nữ là .

Vậy đáp số bài toán là C57 + C47.C13 = 126.