[ĐS & GT] TỔ HỢP - &04. Ôn tập chương 2

 

Hướng dẫn giải.

Bài 55. Gọi số đó là :

• Vì số đõ là chẵn nên có 4 cách chọn c

• Có 7 cách chọn b, có 6 cách chọn c

Theo quy tác nhân có 4.7.6 = 168 số

Bài 56. Gọi số đó là :

• Vì số đó là chẵn nên có 2 cách chọn c

• Có 4 cách chọn b, 3 cách chọn a

Theo quy tắc nhân có 2.3.4 = 24 số

Bài 57.

a) Mỗi công tắc k, 1 ≤ k ≤ 9 có hai trạng thái đóng-mở. Do đó có tất cả 29 = 512 cách đóng-mở công tắc trong mạng điện.

b) Mạch điện được thong từ A đến B khi và chỉ khi có 4 công tắc 1,2,3,4 không cùng mở, 2 công tắc 5 và 6 không cùng mở, 3 công tắc 7,8,9 không cùng mở.

Với 4 công tắc 1,2,3,4 có 24 cách đóng-mở khác nhau. Do đó có 15 cách để thông mạch qua 4 công tắc này (loại bỏ 1 trường hợp cả 4 công tức cùng mở).

Tương tự để thông mạch qua các công tắc 5 và 6 có 22 - 1 cách, để thông mạch qua các công tắc 7,8,9 có 23 - 1

Theo quy tắc nhân ta có: 15.3.7 = 315 cách thông mạch từ A đến B.

Bài 58. Ta đã biết cứ 4 điểm không đồng phẳng xác định 1 tứ diện nhận 4 điểm đó làm đỉnh. Theo giả thiết 9 điểm đã cho không có 4 điểm nào đồng phẳng nên số các tứ diện chính là số tổ hợp chập 4 của 9. Vậy có C49 = 126 tứ diện.

Bài 59.

a) Từ 25 người chọn 4 người bất kì vào ủy ban thường vụ có C425 = 12650 cách.

b) Giả sử 3 người A,B,C được chọn vào các chức vụ đó. Trong 3 người này ai cũng có thể giữ 1 trong 3 chức vụ chủ tịch, phó chủ tịch và thủ quỹ. Do đó có 3! Cách phân công chức vụ. Vì vậy có 3!C325 = 13800 cách thỏa mãn yêu cầu bài toán.

Bài 60.

Bài 61. Không gian mẫu Ω = {0, 1, 2, ...., 998, 999}

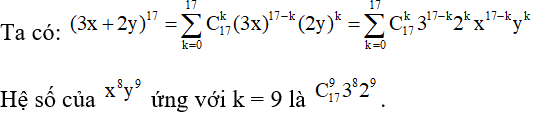
a) Gọi A là biến cố “số chọn ra chia hết cho 3”. Khi đó :

ΩA = {3k|k ∈ N} ⊂ Ω ⇔ ΩA = {3k|k ∈ N,0 ≤ k ≤ 333} ⇒ |ΩA| = 334

Vậy xác xuất của biến cố A là P(A)= 334/1000 = 0,334

b) Gọi B là biến cố “số chọn ra chia hết cho 5”

ΩB = {5k|k ∈ N} ⊂ Ω ⇔ ΩB = {5k|k ∈ N,0 ≤ k ≤ 199} ⇒ |ΩA| = 200

Vậy xác suất của biến cố B là P(B)= 200/1000 = 0,2

Bài 62. Không gian mẫu là Ω gồm tất cả các tập hợp 5 quân bài trong 52 quân bài. Do đó Ω = C552 .

Có đúng 1 cách để chọn đúng quân 2 rô, 1 cách chọn quân 3 pích, 1 cách chọn quân 6 cơ, 1 cách chọn quân 10 nhép và 1 cách chọn quân K cơ. Vậy có đúng 1 cách để chọn 5 quân bài trên

Suy ra xác suất cần tìm là P = 1/(C552)

Bài 63. Ta có |Ω| = C552

Gọi B là biến cố “5 quân bài chọn ra không có quân át nào”. Rõ rang B là biến cố đối của biến cố A “5 quân bài chọn ra có ít nhất 1 con át”

Do đó P(A)= 1 - P(B)

Ta sẽ tính P(B). Số cách chọn ra 5 quân bài không có quân át nào chính là số cách chọn 5 quân bài trong 48 quân bài sau khi đã loại bỏ quân át hay bằng

Vậy P(B)= (C548)/(C552)

Suy ra P(A)=1- (C548)/(C552) = 0,341

Bài 64. Không gian mẫu Ω = {(i; j)|i; j ∈ {1,2,3,4,5}}

Dễ thấy |Ω| = 25

Gọi A là biến cố “tổng 2 số ghi trên 2 thẻ không nhỏ hơn 3” thì biến cố B “tổng 2 số ghi trên 2 thẻ nhỏ hơn 3” là biến cố đối của biến cố A.

Ta có ΩB = {(1,1)} hay |ΩB| = 1

Suy ra P(A) = 1 - P(B) = 1 - 1/25 = 0,96

Bài 65. Không gian mẫu Ω = {(i;j;k)|i,j,k ∈ {1,2,3,4,5}}

|Ω| = 53 = 125

a) Gọi A là biến cố “tổng các số ghi trên 3 thẻ không nhỏ hơn 4”

B là biến cố “tổng các số ghi trên 3 thẻ nhỏ hơn 4”

Ta thấy B = A-

Ta có ΩB = {(1,1,1)} ⇒ |ΩB| = 1

Vậy P(A)=1-P(B)=1- 1/125 = 0,992

b) Gọi C là biến cố “tổng các số ghi trên 3 thẻ bằng 6”

Khi đó : ΩC = {(1,1,4);(1,4,1);(4,1,1);(1,2,3);(1,3,2);(2,1,3);(2,3,1);(3,2,1);(3,1,2)} ⇒ |ΩC| = 10

Vậy P(C)= 10/125 = 0,08

Bài 66.

Bài 67. Ta có X là biến ngẫu nhiên nhận giá trị thuộc tập {5,6,7,8,9,10,11}.

Số phần tử của không gian mẫu là |Ω| = 12

- Tổng 2 số ghi trên 2 thẻ bằng 5 có 1 cặp (1,4) ⇒ P(X = 5) = 1/12

- Tổng 2 số ghi trên 2 thẻ bằng 6 có 2 cặp (1,5);(2,4) ⇒ P(X = 6) = 1/6

- Tổng 2 số ghi trên 2 thẻ bằng 7 có 3 cặp là (1,6);(2,5);(3,4) ⇒ P(X = 7) = 1/4

- Tổng 2 số ghi trên 2 thẻ bằng 8 có 2 cặp là (2,6);(3,5) ⇒ P(X = 8) = 1/6

- Tổng 2 số ghi trên 2 thẻ bằng 9 có 2 cặp là (1,8);(3,6) ⇒ P(X = 9) = 1/6

- Tổng 2 số ghi trên 2 thẻ bằng 10 có 1 cặp là (2,8) ⇒ P(X = 10) = 1/12

- Tổng 2 số ghi trên 2 thẻ bằng 11 có 1 cặp là (3,8) ⇒ P(X = 11) = 1/12

Ta có bảng phân bố xác suất của X:

Áp dụng công thức tính kì vọng ta có:

E(X) = 5/12 + 1 + 7/4 + 8/6 + 9/6 + 10/12 + 11/12 = 7,75

Bài 68.

a) X là biến ngẫu nhiên rời rạc nhận giá trị trong tập {0,1,2,3}

Ta có |Ω| = C37 = 35 phần tử.

• Trong 3 người được chọn không có nữ (X=0) có C34 = 4 cách ⇒ P(X = 0) = 4/35

• Trong 3 người được chọn có 1 nữ (X=1) có C13C24 = 18 cách ⇒ P(X = 1) = 18/35

• Trong 3 người được chọn có 2 nữ (X=2) có C23C14 = 12 cách ⇒ P(X = 2) = 12/35

• Trong 3 người được chọn có 3 nữ (X=3) có 1 cách ⇒ P(X = 3) = 1/35

Ta có bảng phân bố xác suất của X như sau:

b) Áp dụng công thức tính kì vọng và phương sai ta có : E(X) = 9/7; V(X) ≈ 0,49