[ĐS & GT] Lượng giác - 02.Phương trình lượng giác (phần 1)
Hướng dẫn giải.
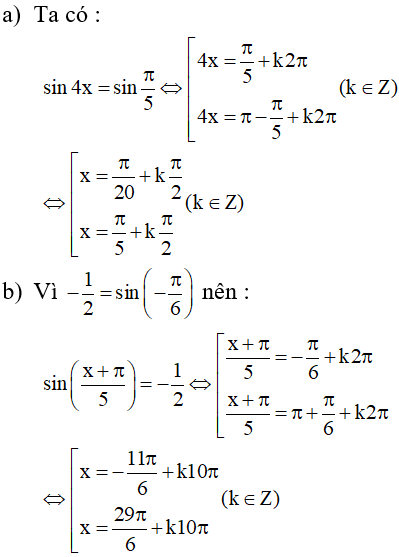
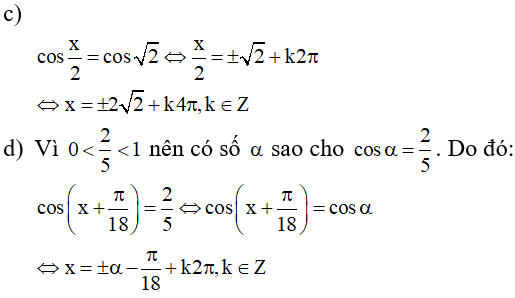
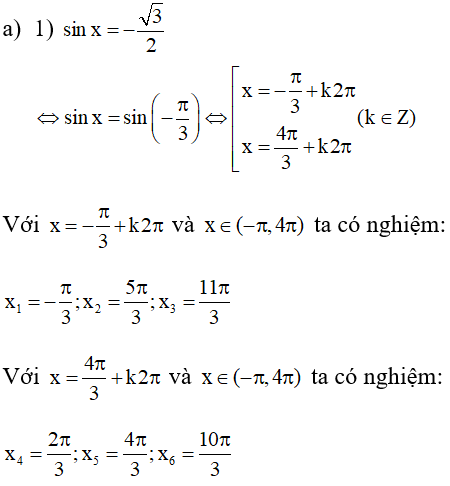



a)
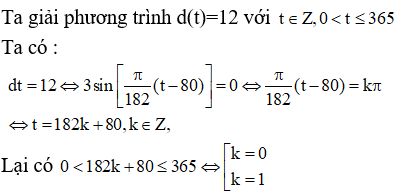
Vậy thành phố A có đúng 12 giờ có ánh sáng mặt trời vào ngày thứ 30 (ứng với k = 0) và ngày thứ 262 (ứng với k = 1) trong năm.
b)

Vậy nên thành phố A có ít giờ có ánh sáng mặt trời nhất (9 giờ) vào ngày thứ 353 trong năm.
c)

Vậy nên thành phố A có nhiều giờ có ánh sáng mặt trời nhất (15 giờ) vào ngày thứ 171 trong năm.
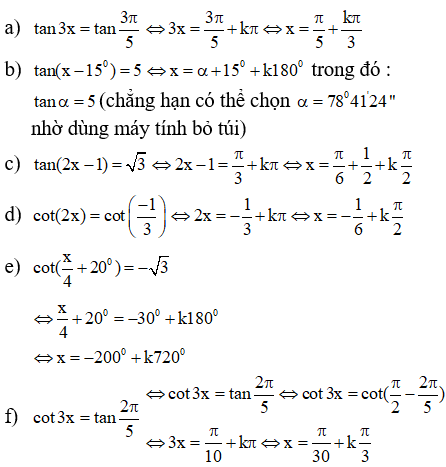
a)
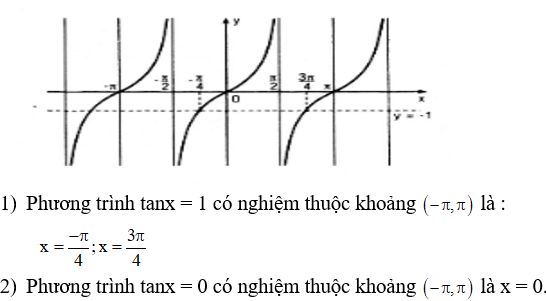
b)
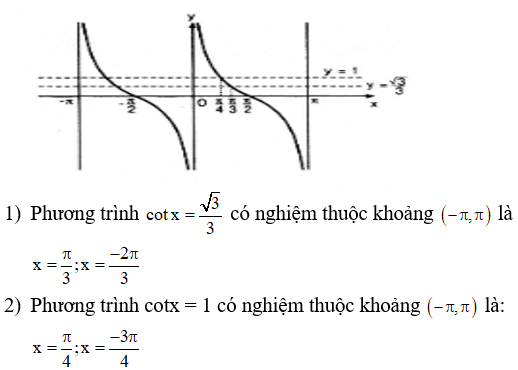
a)
tan(2x - 15o) = 1 ⇔ 2x = 15o + 45o + k180o ⇔ x = 30o + k90o
- 180o < 30o + k90o ⇔ -2 < 1/3 + k < 1 ⇔ k ∈ {-2, 1, 0}
Vậy các nghiệm của phương trình là x = -150o, x = -60o, x = 30o
b)

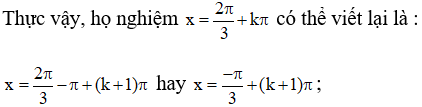
đây chính là kết quả mà Phương tìm được.
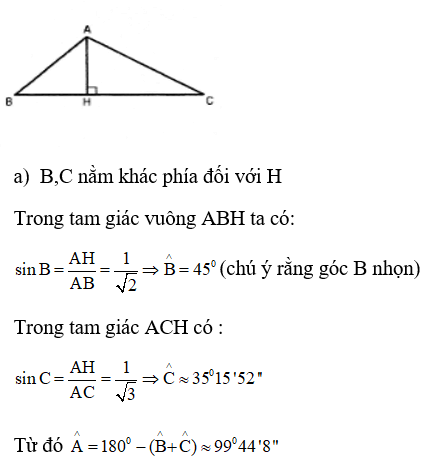

Bài đọc thêm (tiếp theo). Sử dụng Máy tính cầm tay
Hướng dẫn giải.
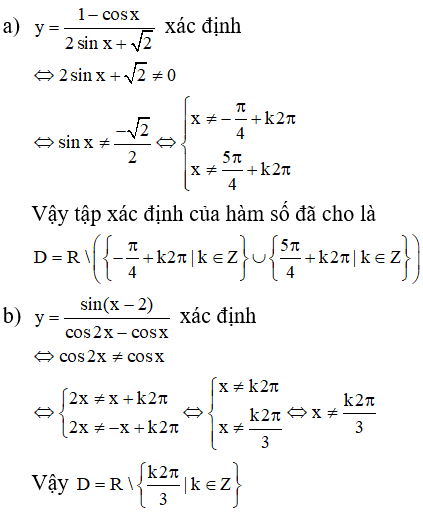
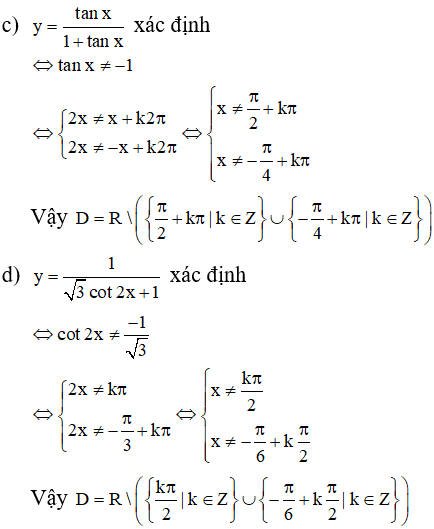
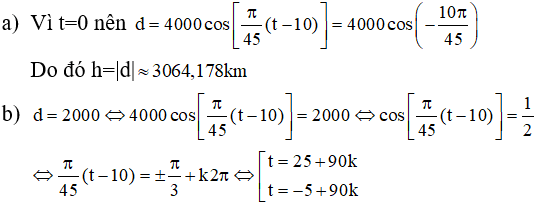
Chú ý rằng t > 0 ta thấy ngay giá trị nhỏ nhất của t là t = 25. Vậy d = 2000 km xảy ra lần đầu tiên sau khi phóng con tàu vũ trụ vào quỹ đạo được 25 phút.
c)
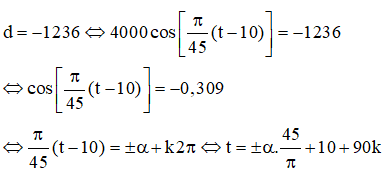
Trong đó k ∈ Z, cosα = -0,309
Sử dụng bảng số hoặc máy tính bỏ túi , ta có thể chọn α = 1,885 . khi đó ta có: t = ±27000 + 10 + 90k tức là t = -17000 + 90k hoặc t = 37000+90k. Dễ thấy giá trị dương nhỏ nhất của t là 37000. Vậy d = -1236km xảy ra lần đầu tiên là 37000 phút sau khi con tàu được phóng vào quỹ đạo.
a) Chiếc gầu ở vị trí thấp nhất khi
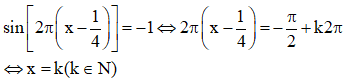
Điều đó chứng tỏ chiếc gầu ở vị trí thấp nhất vào các thời điểm 0 phút; 1 phút; 2 phút; 3 phút….
b) Chiếc gầu ở vị trì cao nhất khi
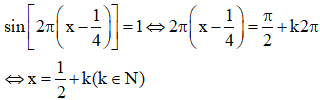
Điều đó chứng tỏ chiếc gầu ở vị trí thấp nhất vào các thời điểm 0,5 phút; 1,5 phút; 2,5 phút; 3,5 phút….
c) Chiếc gầu cách mặt nước 2m khi .
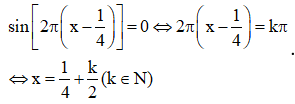
Do đó lần đầu tiên nó cách mặt nước 2m khi quay được ¼ phút (ứng với k = 0)
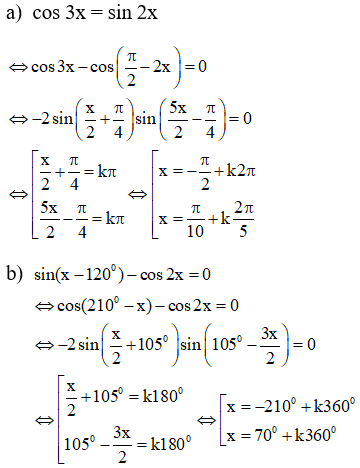
Hướng dẫn giải.
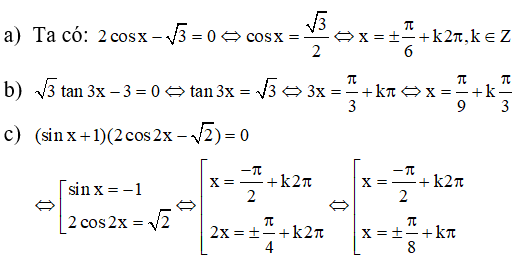
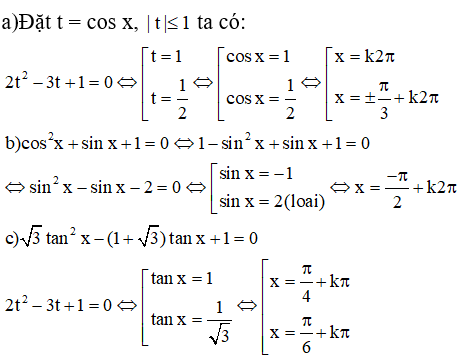
a) 3cos2x + 10sinx + 1 = 0
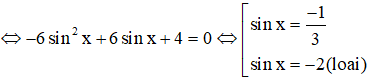
Phương trình sinx = -1/3 có nghiệm gần đúng là x = -0,34
b)
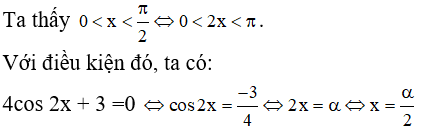
Trong đó α là số thực thuộc khoảng (0; π) thỏa mãn cosα = -3/4 . Dùng bảng số hoặc máy tính bỏ túi ta tìm được α ≈ 2,42. Từ đó nghiệm gần đúng của phương trình là x ≈ 1,21.
c)
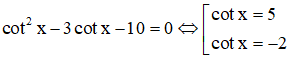
Nghiệm gần đúng của phương trình trong khoảng (0; π) là x ≈ 0,2 và x ≈ 2,68
d)
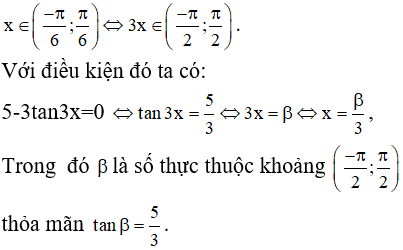
Dùng bảng số hoặc máy tính bỏ túi ta tìm được β ≈ 1,03. Từ đó nghiệm gần đúng của phương trình là x ≈ 0,34.
a) Chia 2 vế của phương trình cho √(32 + 42) = 5 ta được:
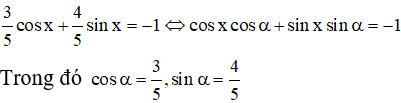
Ta có cos(x - α) = -1 ⇔ x - α = π + k2π ⇔ x = α + π + k2π
b) Chia 2 vế của phương trình cho √(22 + 22) = 2√2 ta được:
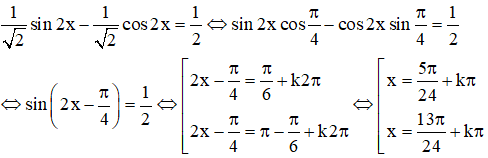
c) 5sin2x - 6cos2x = 13 ⇔ 5sin2x - 3(1 + cos2x) = 13 ⇔ 5sin2x - 3cos2x = 16

Vậy phương trình đã cho vô nghiệm.
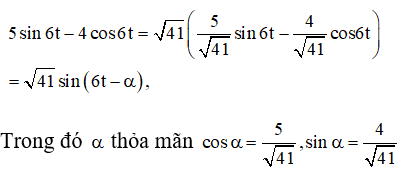
Sử dụng bảng số hoặc máy tính bỏ túi ta tìm được α ≈ 0,675.
a) Vật ở vị trí cân bằng khi d = 0, nghĩa là sin(6t - α) = 0
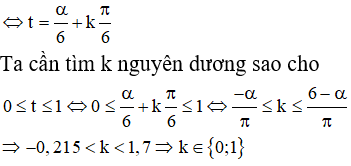
Vậy trong khoảng thời gian 1 giây đầu tiên có 2 lần vật ở vị trí cân bằng là t ≈ 0,11 giây (ứng với k = 0) và t ≈ 0,64 giây (ứng với k = 1).
b) Vật ở xa vị trí cân bằng nhất khi |d| nhận giá trị lớn nhất. Điều đó xảy ra nếu sin(6t - α) = ±1 . Ta có:

Vậy trong khoảng thời gian 1 giây đầu tiên có 2 lần vật ở xa vị trí cân bằng nhất là t ≈ 0,37 giây (ứng với k = 0) và t ≈ 0,90 giây (ứng với k = 1).
a) Ta có :
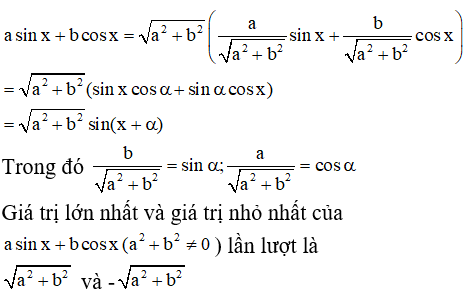
b) Ta có:
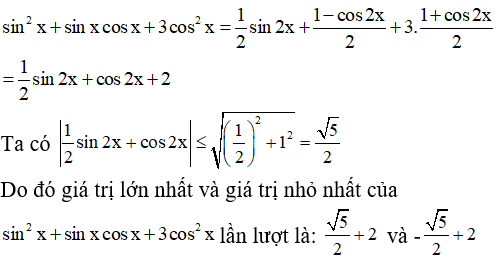
c) Ta có:
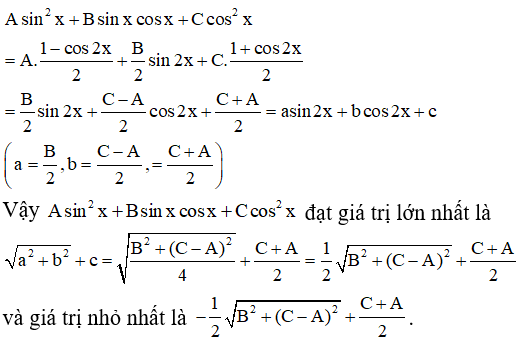
a) cosx = 0 không thỏa mãn phương trình
Chia cả 2 vế của phương trình cho cos2x ≠ 0 ta được:
2tan2x + 3√3tanx - 1 = 4(1 + tan2x)
⇔ 2tan2x + 3√3tanx + 5 = 0
Phương trình vô nghiệm nên phương trình đã cho vô nghiệm.
b) cosx = 0 không thỏa mãn phương trình.
Chia cả 2 vế của phương trình cho cos2x ≠ 0 ta được:
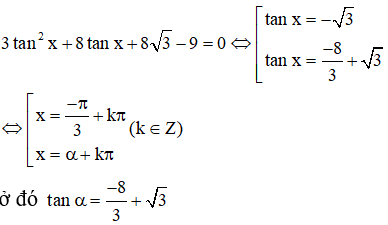
c) cosx=0 không thỏa mãn phương trình.
Chia cả 2 vế của phương trình cho cos2x ≠ 0 ta được:
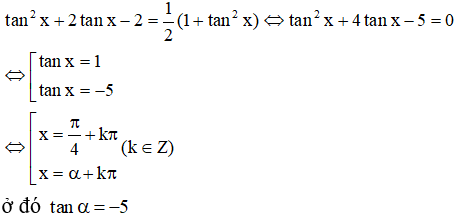
a) cosxcos5x = cos2xcos4x
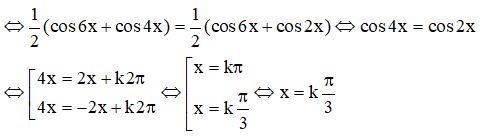
b) cos5xsin4x = cos3xsin2x
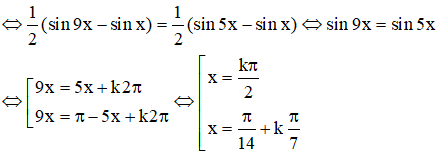
c) sin2x + sin4x = sin6x
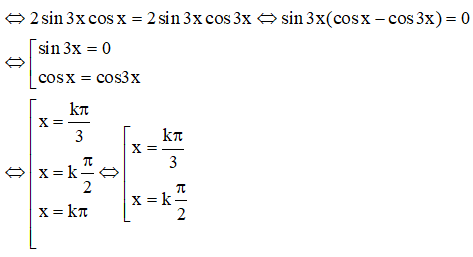
d) sinx + sin2x = cosx + cos2x
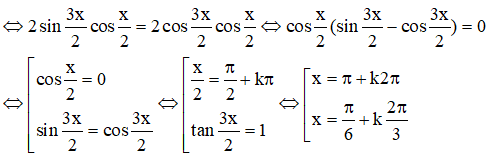
a) sin24x + sin23x = sin22x + sin2x
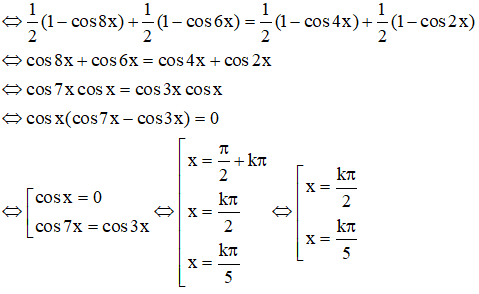
b) cos2x + cos22x + cos23x + cos24x = 2
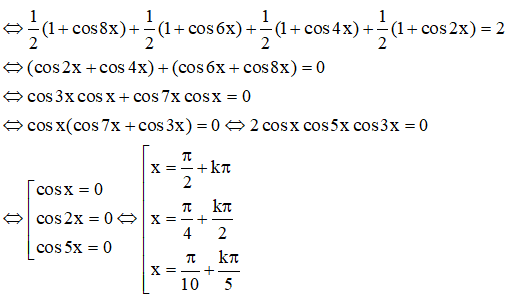
a)
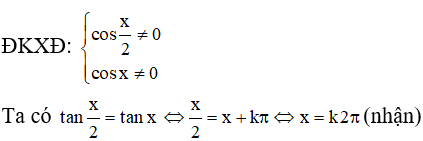
b)
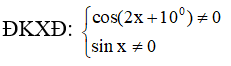
tan(2x + 10o) + cotx = 0 ⇔ tan(2x + 10o) = tan(90o + x)
⇔ 2x + 10o = 90o + x + k.180o ⇔ x = 80o + k.180o
Hiển nhiên x = 80o + k.180o thỏa mãn ĐKXĐ.
Vậy phương trình đã cho có nghiệm x = 80o + k.180o
c)
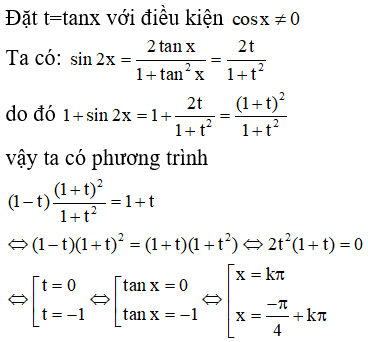
d) v
e) ĐKXĐ: cosx ≠ 0, sin2x ≠ 0, sin4x ≠ 0 nhưng chỉ cần sin4x ≠ 0 là đủ vì sin4x = 2sin2xcos2x = 4sinxcosxcos2x. Với điều kiện đó ta có:
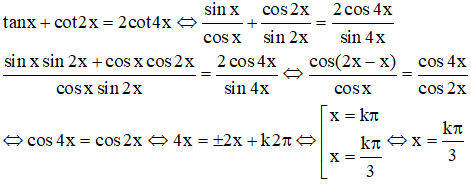
Để là nghiệm các giá trị này còn phải thỏa mãn sin4x ≠ 0 . Ta có:
- Nếu k chia hết cho 3 tức là k = 3m, thì sin4x = sin4mπ = 0
- Nếu k không chia hết cho 3, tức là k = 3m + 1 , m ∈ Z thì :
a) Người chơi đu ở xa vị trí cân bằng nhất khi :
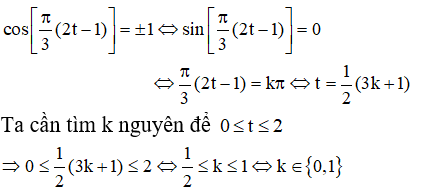
Với k = 0 thì t= 1/2 , với k = 1 thì t = 2. Vậy trong 2 giây đầu tiên người chơi đu ở xa vị trí cân bằng nhất vào các thời điểm 1/2 giây và 2 giây.
b) Người chơi đu cách vị trí cân bằng 2 mét khi :
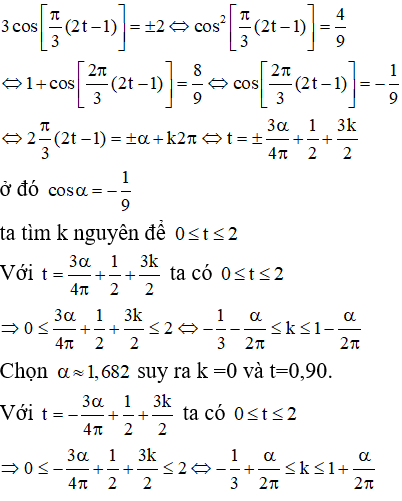
Chọn α ≈ 1,682, suy ra k = 0;1.
Với k = 0 ta có t = 0,10; với k = 1 ta có t = 1,60.
Kết luận: trong 2 giây đầu tiên có 3 thời điểm mà người chơi đu cách vị trí cân bằng 2 mét là t = 0,10 giây; t= 0,90 giây và t = 1,60 giây.
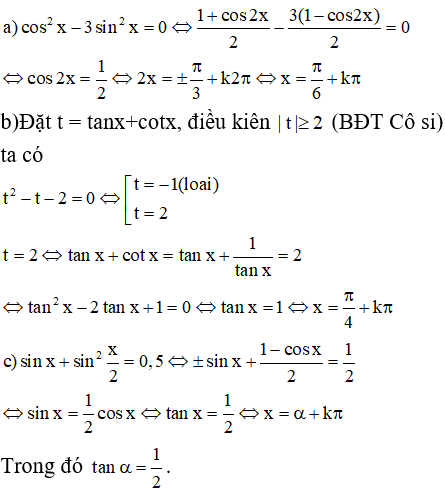
a)
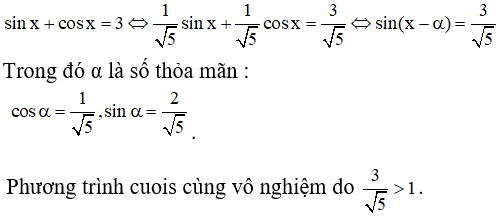
Vậy phương trình đã cho vô nghiệm.
b) Trong phương trình 5sin2x + sinx + cosx +6 =0 ta đặt t = sinx + cosx với điều kiện |t| ≤ √2 thì được phương trình 5t2 + t + 1 = 0 . Phương trình này vô nghiệm nên phương trình đã cho vô nghiệm.








a) Đúng vì hàm số y = sinx, y = cosx có cùng tập xác định D=R.
b) Sai vì y=tanx xác định với mọi x ≠ π/2 + kπ còn y=cotx xác định với mọi x ≠ kπ
c) Đúng
d) Sai vì y=cotx là hàm số lẻ
e) Sai vì y=cosx không nghịch biến trên khoảng (π/2; 3π/2)
f) Đúng
Sai vì trên khoảng (-π/2; π/2) hàm số y=tanx đồng biến nhưng hàm số y=cotx không nghịch biến.
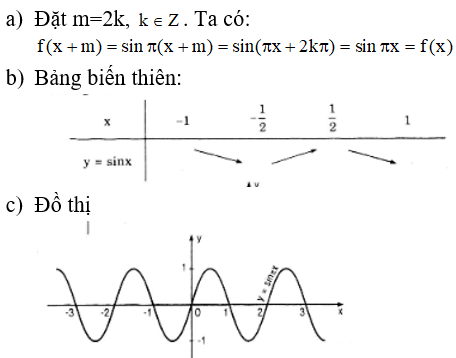
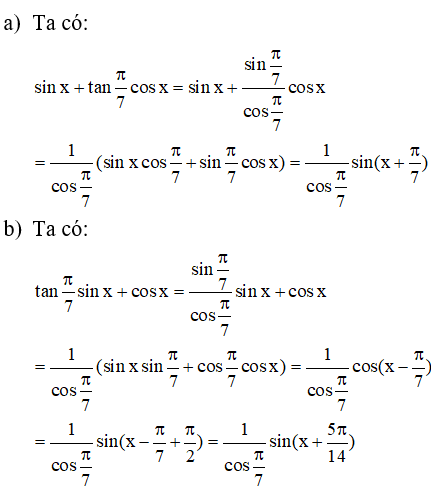
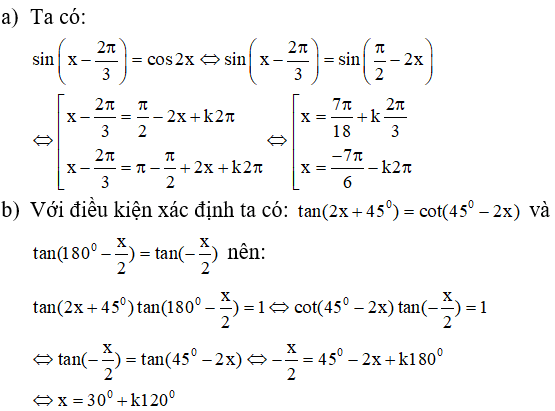
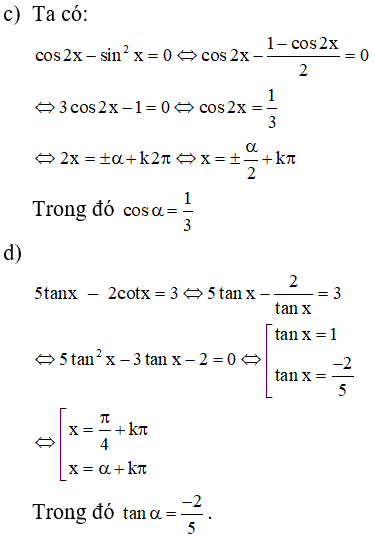
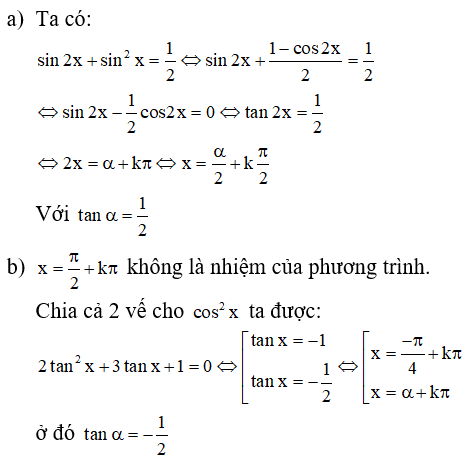
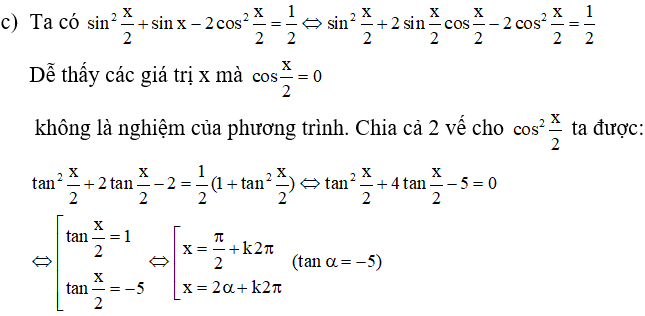
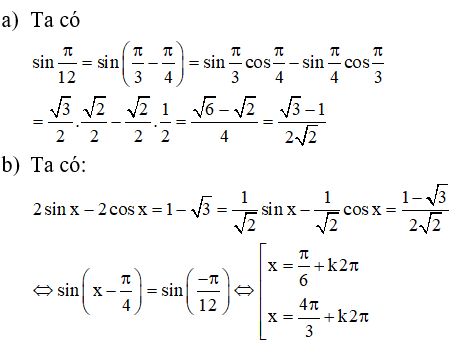
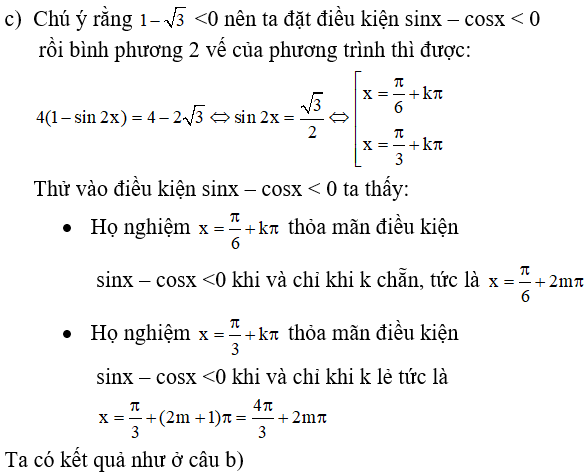
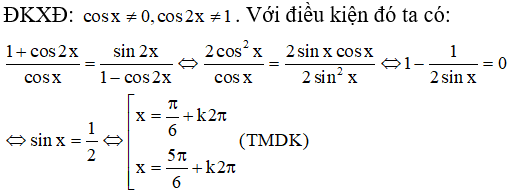





































Nhận xét
Đăng nhận xét