[HH8] TỨ GIÁC - &01. Hình thang. Đường trung bình. Dựng hình. Phép đối xứng trục
Hướng dẫn giải.
+ Hình 5a: Áp dụng định lý trong tứ giác ABCD ta có: x + 110º + 120º + 80º = 360º
⇒ x = 360º – 110º – 120º – 80º = 50º
+ Hình 5b:Dựa vào hình vẽ ta có:
Áp dụng định lý trong tứ giác EFGH ta có: x + 90º + 90º + 90º = 360º
⇒ x = 360º – 90º – 90º – 90º = 90º.
+ Hình 5c:Dựa vào hình vẽ ta có:
Áp dụng định lý trong tứ giác ABDE ta có: x + 90º + 65º + 90º = 360º
⇒ x = 360º – 90º – 65º – 90º = 115º
+ Hình 5d:
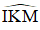


Áp dụng định lý trong tứ giác IKMN ta có: x + 90º + 120º + 75º = 360º
⇒ x = 360º – 90º – 120º – 75º = 75º
+ Hình 6a: Áp dụng định lý trong tứ giác PQRS ta có: x + x + 65º + 95º = 360º
⇒ 2x + 160º = 360º ⇒ 2x = 200º ⇒ x = 100º
+ Hình 6b: Áp dụng định lý trong tứ giác MNPQ ta có: x + 2x + 3x + 4x = 360º
⇒ 10x = 360º ⇒ x = 36º.
a) + Góc ngoài tại A là góc A1:
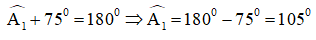
+ Góc ngoài tại B là góc B1:
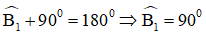
+ Góc ngoài tại C là góc C1:
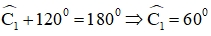
+ Góc ngoài tại D là góc D1:
Theo định lý tổng các góc trong một tứ giác bằng 360º ta có:
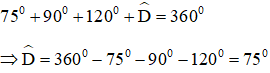
Lại có:
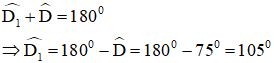
Vậy góc ngoài tại D bằng 105º.
b) Hình 7b:
Ta có:
Mà theo định lý tổng bốn góc trong một tứ giác bằng 360º ta có:
c) Nhận xét: Tổng các góc ngoài của tứ giác cũng bằng 360º.
a) Ta có: AB = AD (gt) ⇒ A thuộc đường trung trực của BD
CB = CD (gt) ⇒ C thuộc đường trung trực của BD
Vậy AC là đường trung trực của BD
b) Xét ΔABC và ΔADC có: AB = AD (gt); BC = DC (gt); AC cạnh chung
⇒ ΔABC = ΔADC (c.c.c)
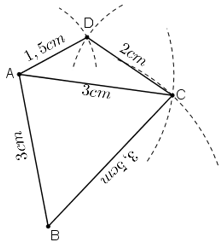
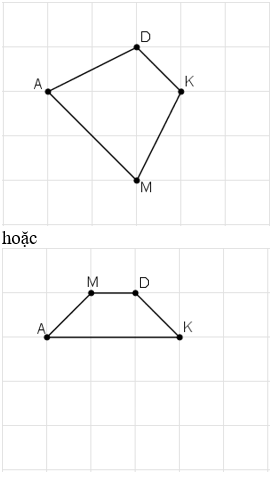
- Cách vẽ hình 9:
+ Vẽ đoạn thẳng AB = 3cm
+ Quay cung tròn tâm A, bán kính 3cm, cung tròn tâm B bán kính 3,5cm. Hai cung tròn này cắt nhau tại C.
+ Quay cung tròn tâm C bán kính 2cm và cung tròn tâm A bán kính 1,5cm. Hai cung tròn này cắt nhau tại D.
+ Nối các đoạn BC, AC, CD, AD ta được hình cần vẽ.
- Cách vẽ hình 10:
+ Vẽ góc 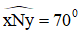
+ Vẽ cung tròn tâm P bán kính 1,5cm và cung tròn tâm M bán kính 3cm. Hai cung tròn này cắt nhau tại Q.
+ Nối PQ, MQ ta được hình cần vẽ.
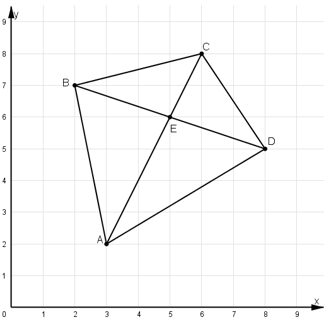
+ Xác định các điểm A, B, C, D trong hệ trục tọa độ như trên hình vẽ.
+ Hai đường chéo của tứ giác là AC và BD.
+ Vị trí kho báu là giao điểm của AC và BD và là điểm E trên hình vẽ.
+ Nhìn trên hình vẽ thấy điểm E có tọa độ (5; 6)
Vậy vị trí tọa độ của kho báu là (5; 6)
Hướng dẫn giải.
+ Tứ giác ABCD có AB // CD nên là hình thang.
+ Tứ giác EFGH không có hai cạnh nào song song nên không phải hình thang.
+ Tứ giác KMNI có KM // IN nên là hình thang.
+ Hình 21a): AB // CD ⇒ 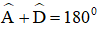
hay x + 80º = 180º ⇒ x = 100º.
Lại có: AB // CD ⇒ 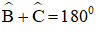
hay 40º + y = 180º ⇒ y = 140º.
+ Hình 21b): AB // CD ⇒ x = 70º (Hai góc đồng vị bằng nhau)
AB // CD ⇒ y = 50º (Hai góc so le trong bằng nhau)
+ Hình 21c): AB // CD ⇒ 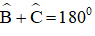
hay x + 90º = 180º ⇒ x = 90º
AB // CD ⇒ 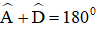
hay y + 65º = 180º ⇒ y = 115º.
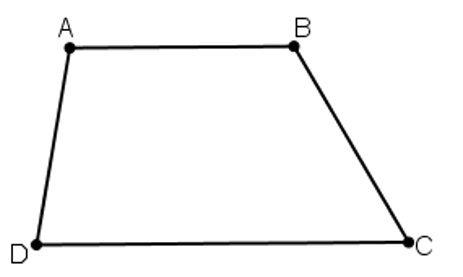


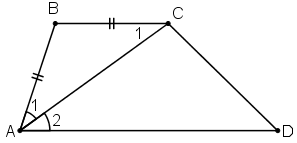
* Để chứng minh ABCD là hình thang ta cần chứng minh AD // BC.
Thông thường để chứng minh hai đường thẳng song song ta có thể chọn một trong các cách:
+ Chứng minh hai góc so le trong bằng nhau hoặc hai góc đồng vị bằng nhau.
+ Chứng minh hai đường thẳng cùng song song hoặc cùng vuông góc với đường thẳng thứ ba.
Ở bài này ta sẽ đi chứng minh hai góc so le trong bằng nhau là góc A2 và C1.
Theo giả thiết ta có:
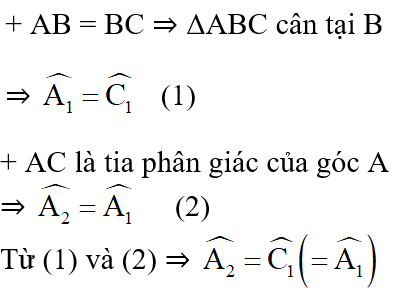
Mà hai góc này ở vị trí so le trong ⇒ AD // BC
Vậy ABCD là hình thang (đpcm).
Hướng dẫn giải.
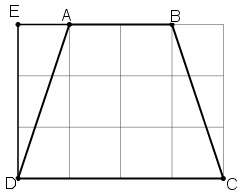
(Mỗi ô vuông là 1cm).
Nhìn vào hình vẽ ta thấy :
+ AB = 2cm
+ CD = 4cm.
+ Tính AD : Xét tam giác vuông ADE có AE = 1cm, DE = 3cm.
⇒ AD2 = AE2 + DE2 (Định lý Pytago) = 12 + 32 = 10 ⇒ AD = √10 cm
+ Tính BC : ABCD là hình thang cân nên BC = AD = √10 cm.
Vậy AB = 2cm, CD = 4cm, AD = BC = √10 cm.

Vì hình thang ABCD cân
AD = BC;
Ĉ = D̂
Xét hai tam giác vuông AED và BFC có: AD = BC; Ĉ = D̂
⇒ ΔAED = ΔBFC (cạnh huyền – góc nhọn) ⇒ DE = CF.
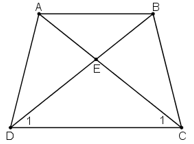
Do ABCD là hình thang cân nên: AD = BC; AC = BD;
Xét hai tam giác ADC và BCD, ta có: AD = BC (gt) ; AC = BD (gt); DC cạnh chung
⇒ ΔADC = ΔBCD (c.c.c)
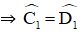
⇒ ΔECD cân tại E ⇒ EC = ED.
Mà AC = BD
⇒ AC – EC = BD – ED hay EA = EB.
Vậy EA = EB, EC = ED.
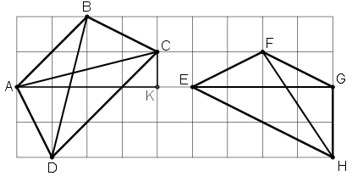
+ Xét tứ giác ABCD
Nhận thấy AB // CD ⇒ Tứ giác ABCD là hình thang.
Xét ΔACK vuông tại K ta có: AC2 = AK2 + KC2 = 42 + 12 = 17
Tương tự ta có BD2 = 42 + 12 = 17 ⇒ AC2 = BD2 ⇒ AC = BD
Vậy hình thang ABCD có hai đường chéo AC = BD nên là hình thang cân.
+ Xét tứ giác EFGH
FG // EH ⇒ Tứ giác EFGH là hình thang.
Lại có : EG = 4cm
FH2 = 22 + 32 = 13 ⇒ FH = √13 ≠ EG.
Vậy hình thang EFGH có hai đường chéo không bằng nhau nên không phải hình thang cân.
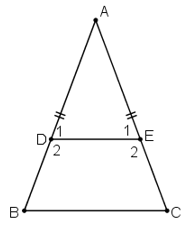
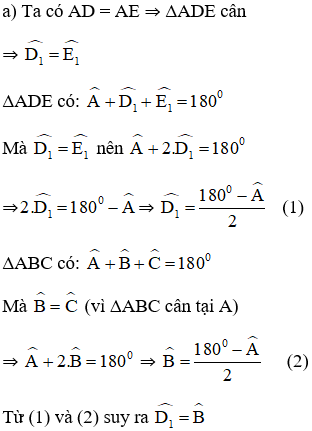
Mà hai góc ở vị trí đồng vị ⇒ DE // BC ⇒ Tứ giác DECB là hình thang.
Mà hai góc ở đáy B và C bằng nhau nên hình thang DECB là hình thang cân.
b)
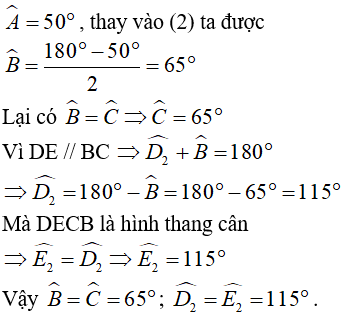
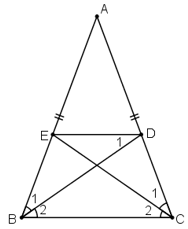
- Chứng minh tứ giác BCDE là hình thang cân:
+ ΔABC cân tại A
BD là phân giác của
CE là phân giác của
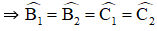
+ Xét ΔAEC và ΔADB có:
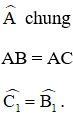
⇒ ΔAEC = ΔADB ⇒ AE = AD
Vậy tam giác ABC cân tại A có AE = AD
Theo kết quả bài 15a) suy ra BCDE là hình thang cân.
- Chứng minh ED = EB.
ED // BC ⇒ 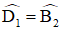
Mà 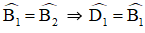
Vậy ta có EBCD là hình thang cân có đáy nhỏ bằng cạnh bên.
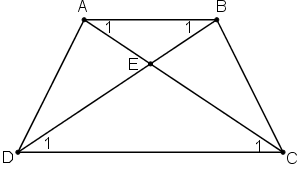
Gọi E là giao điểm của AC và BD.
+ 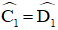
+ AB//CD ⇒ 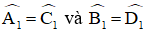
Mà
⇒ ΔEAB cân tại E ⇒ EA = EB (2)
Từ (1) và (2) suy ra: EA + EC = EB + ED hay AC = BD.
Vậy hình thang ABCD có hai đường chéo AC = BD nên là hình thang cân.
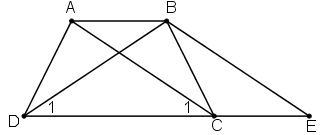
a) Hình thang ABEC (AB//CE) có hai cạnh bên AC, BE song song nên chúng bằng nhau: AC = BE (1)
Theo giả thiết AC = BD (2)
Từ (1) và (2) suy ra BE = BD do đó ΔBDE cân
Vậy hình thang ABCD có hai góc kề một đáy bằng nhau nên là hình thang cân.
Hướng dẫn giải.
+ K̂ = Ĉ (= 50º) ⇒ IK // BC (Vì có hai góc đồng vị bằng nhau)
+ KA = KC (= 8cm) nên K là trung điểm AC
Đường thẳng IK đi qua trung điểm cạnh AC và song song với cạnh BC nên đi qua trung điểm cạnh AB
⇒ I là trung điểm AB ⇒ IA = IB hay x = 10cm.
⇒ CD là đường trung bình của ΔOAB ⇒ AB = 2CD = 2.3 = 6cm.
⇒ EM // DC hay EM // DI.
ΔAEM có DI // EM (cmt) và AD = DE (gt) ⇒ IA = IM (Theo định lý 1)
* Ba đường thẳng MP, NQ và IK cùng vuông góc với PQ => MP// IK// NQ
=> Tứ giác MPQN là hình thang
Do đường thẳng IK đi qua trung điểm cạnh bên MN và song song với hai đáy nên K là trung điểm PQ.
Nên PK = KQ =5dm
Vậy x = 5dm
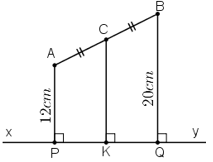
Gọi P, Q, K lần lượt là chân đường vuông góc hạ từ A, B, C xuống xy.
+ AP ⊥ xy và BQ ⊥ xy ⇒ AP // BQ ⇒ Tứ giác ABQP là hình thang.
+ CK ⊥ xy ⇒ CK // AP//BQ
+ Hình thang ABQP có AC = CB (gt) và CK // AP // BQ ⇒ PK = KQ
⇒ CK là đường trung bình của hình thang ⇒ CK = (AP + BQ)/2.
Mà AP = 12cm, BQ = 20cm ⇒ CK = 16cm.
Vậy khoảng cách từ trung điểm C của AB đến xy bằng 16cm.
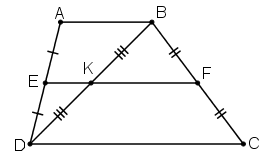
+ ΔABD có DE = EA và DK = KB ⇒ EK là đường trung bình của ΔDAB ⇒ EK // AB
+ Hình thang ABCD có: AE = ED và BF = FC
⇒ EF là đường trung bình của hình thang ABCD ⇒ EF // AB// CD
+ Qua điểm E ta có EK // AB và EF // AB nên theo tiên đề Ơclit ta có E, K, F thẳng hàng.
+ Tính x : AB // EF nên tứ giác ABFE là hình thang
Hình thang ABFE có: CA = CE và DB = DF
⇒ CD là đường trung bình của hình thang ABFE ⇒ CD = (AB + EF)/2
hay x = (8 + 16)/2 = 12(cm)
+ Tính y: CD // GH nên tứ giác CDHG là hình thang
Hình thang CDHG có : EC = EG, FD = FH
⇒ EF là đường trung bình của hình thang CDHG ⇒ EF = (CD + GH)/2
hay (x + y)/2 = 16cm ⇒ x + y = 32cm
Mà x = 12cm ⇒ y = 20cm.
Vậy x = 12cm và y = 20cm.
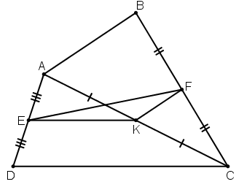
a) + ΔADC có: AE = ED (gt) và AK = KC (gt) ⇒ EK là đường trung bình của ΔADC
⇒ EK = CD/2
+ ΔABC có AK = KC (gt) và BF = FC (gt) ⇒ KF là đường trung bình của ΔABC
⇒ KF = AB/2.
b) Ta có: EF ≤ EK + KF =
(Bổ sung: 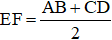
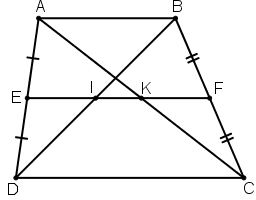
a) + Hình thang ABCD có EA = ED, FB = FC (gt)
⇒ EF là đường trung bình của hình thang ABCD. ⇒ EF // AB // CD
+ ΔABC có BF = FC (gt) và FK // AB (cmt) ⇒ AK = KC
+ ΔABD có: AE = ED (gt) và EI // AB (cmt) ⇒ BI = ID
b) + Vì EF là đường trung bình của hình thang ABCD.
⇒ EF = (AB + CD)/2 = (6 + 10)/2 = 8cm.
+ ΔABD có AE = ED, DI = IB ⇒ EI là đường trung bình của ΔABD
⇒ EI = AB/2 = 6/2 = 3(cm)
+ ΔABC có CF = BF, CK = AK ⇒ KF là đường trung bình của ΔABC
⇒ KF = AB /2 = 6/2 = 3cm
+ Lại có: EI + IK + KF = EF ⇒ IK = EF – EI – KF = 8 – 3 – 3 = 2cm
Hướng dẫn giải.
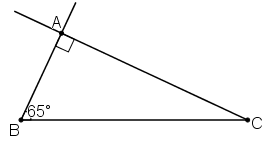
a) Phân tích
Giả sử dựng được ΔABC thỏa mãn yêu cầu đề bài.
Đoạn thẳng BC dựng được vì đã biết độ dài.
Khi đó điểm A là giao điểm của:
+ Tia Bx tạo với đoạn thẳng BC góc 65º
+ Đường thẳng qua C và vuông góc với tia Bx vừa dựng.
b) Cách dựng:
- Dựng đoạn thẳng BC = 4cm.
- Dựng tia Bx tạo với BC một góc 65º.
- Dựng đường thẳng a qua C và vuông góc với Bx.
- Bx cắt a tại A.
ΔABC là tam giác cần dựng.
c) Chứng minh: ΔABC vừa dựng vuông tại A, góc B = 65º và BC = 4cm.
d) Biện luận: Ta luôn dựng được một tam giác thỏa mãn điều kiện đề bài.
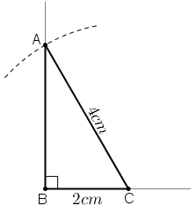
a) Phân tích:
Giả sử dựng được ΔABC thỏa mãn yêu cầu.
Ta dựng được đoạn BC vì biết BC = 2cm.
Khi đó điểm A là giao điểm của:
+ Tia Bx vuông góc với BC
+ Cung tròn tâm C bán kính 4cm.
b) Cách dựng:
+ Dựng đoạn thẳng BC = 2cm.
+ Dựng tia Bx vuông góc với cạnh BC.
+ Dựng cung tròn tâm C, bán kính 4cm. Cung tròn cắt tia Bx tại A.
Kẻ AC ta được ΔABC cần dựng.
c) Chứng minh
ΔABC có góc B = 90º, BC = 2cm.
A thuộc cung tròn tâm C bán kính 4cm nên AC = 4cm.
Vậy ΔABC thỏa mãn yêu cầu đề bài
d) Biện luận: Ta luôn dựng được một hình thang thỏa mãn điều kiện của đề bài.
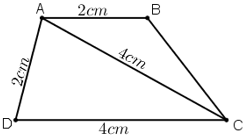
a) Phân tích :
Giả sử dựng được hình thang ABCD thỏa mãn yêu cầu đề bài.
Tam giác ADC dựng được vì biết ba cạnh của tam giác.
Điểm B phải thỏa mãn hai điều kiện :
+ B nằm trên tia Ax song song với CD
+ B cách A một đoạn 2cm.
b) Cách dựng:
+ Dựng tam giác ADC có AD = 2cm, AC = 4cm, CD = 4cm.
+ Dựng tia Ax song song với CD và nằm trên cùng một nửa mặt phẳng chứa điểm C bờ là đường thẳng AD.
+ Trên tia Ax lấy điểm B sao cho AB = 2cm.
Kẻ BC ta được hình thang ABCD cần dựng.
c) Chứng minh
Tứ giác ABCD là hình thang vì AB // CD.
Hình thang ABCD có AB = AD = 2cm, AC = BC = 4cm thỏa mãn yêu cầu đề bài
d) Biện luận: Ta luôn dựng được một hình thang thỏa mãn yêu cầu của đề bài.
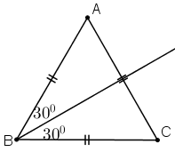
a) Phân tích
Để dựng một góc 30º, ta dựng góc 60º rồi dựng tia phân giác của góc đó.
Để dựng góc 60º, ta dựng tam giác đều với độ dài cạnh bất kì.
b) Cách dựng:
- Dựng tam giác đều ABC cạnh bất kì (Ví dụ 2cm)
- Dựng tia phân giác Bx của góc
Ta được góc
c) Chứng minh
ΔABC đều nên
Bx là tia phân giác của 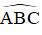
Vậy ta dựng được góc 30º thỏa mãn yêu cầu đề bài.
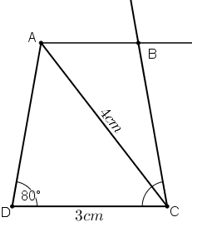
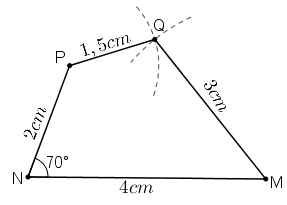
a) Phân tích
Giả sử dựng được hình thang ABCD theo yêu cầu đề bài.
Ta dựng được đoạn thẳng CD = 3cm.
Điểm A phải thỏa mãn hai điều kiện:
+ Tia DA tạo với DC một góc bằng 80º.
+ CA = 4cm nên A thuộc cung tròn tâm C bán kính 4cm.
ABCD là hình thang nên AB // CD
Hình thang ABCD cân nên
Vì vậy điểm B phải thỏa mãn 2 điều kiện:
+ B nằm trên đường thẳng đi qua A và song song với CD
+ Tia CB tạo với CD một góc 80º.
b) Cách dựng
+ Dựng đoạn CD = 3cm.
+ Dựng tia Dx thỏa mãn
+ Dựng cung tròn tâm C, bán kính 4cm cắt tia Dx tại A.
+ Qua A dựng đường thẳng m song song với CD.
+ Dựng tia Cy trên cùng nửa mặt phẳng chứa điểm A, bờ CD thỏa mãn
+ Tia Cy cắt đường thẳng m tại B.
Ta dựng được hình thang ABCD
c) Chứng minh
+ Tứ giác ABCD là hình thang vì AB // CD
+ Hình thang ABCD có 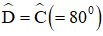
+ Hình thang cân ABCD có CD = 3cm, AC = 4cm, 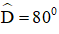
d) Biện luận: Ta luôn dựng được một hình thang thỏa mãn điều kiện đề bài.
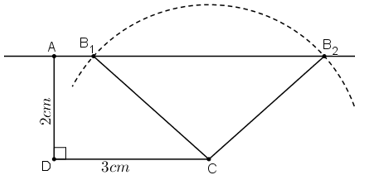
a) Phân tích
Giả sử dựng được hình thang ABCD thỏa mãn yêu cầu đề bài.
Ta dựng được tam giác ADC vì biết hai cạnh và góc xen giữa.
Điểm B phải thỏa mãn hai điều kiện:
+ B nằm trên đường thẳng qua A và song song với CD
+ CB = 3cm nên B thuộc cung tròn tâm C bán kính 3cm.
b) Cách dựng:
- Dựng tam giác ADC vuông tại D với DC = 3cm, DA = 2cm.
- Dựng tia Ax // CD (tia Ax về phía C).
- Dựng (C; 3cm) cắt tia Ax tại hai điểm B1 và B2.
Hình thang ABCD với B trùng với B1 hoặc B trùng với B2 là hình thang cần dựng.
c) Chứng minh: Theo cách dựng thì tứ giác ABCD hoặc AB1CD có góc ∠D = 90º, đáy CD = 3cm, cạnh bên AD = 2cm, cạnh bên BC = 3cm nên đó là hình thang vuông thỏa mãn điều kiện đề bài.
d) Biện luận: Ta dựng được hai hình thang thỏa mãn điều kiện đề bài.
Hướng dẫn giải.
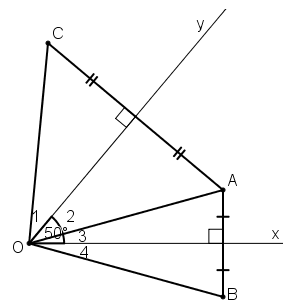
a) + B đối xứng với A qua Ox ⇒ Ox là đường trung trực của AB ⇒ OA = OB (1)
+ C đối xứng với A qua Oy ⇒ Oy là đường trung trực của AC ⇒ OA = OC (2)
Từ (1) và (2) suy ra OB = OC (= OA)
b) + ΔOAC cân tại O có Oy là đường trung trực ⇒ Oy đồng thời là đường phân giác
+ ΔOAB cân tại O có Ox là đường trung trực
⇒ Ox đồng thời là đường phân giác
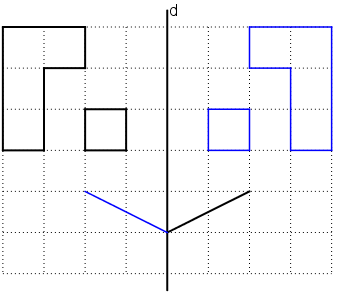
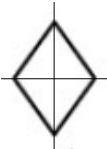
+ Hình a có hai trục đối xứng:
+ Hình b có một trục đối xứng

+ Hình c có một trục đối xứng

+ Hình d có một trục đối xứng

+ Hình e có một trục đối xứng
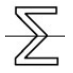
+ Hình g có năm trục đối xứng

+ Hình h không có trục đối xứng
+ Hình i có một trục đối xứng
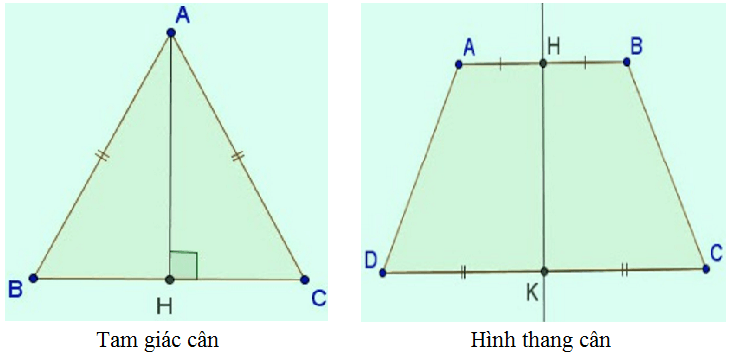
- ΔABC cân tại A có trục đối xứng là đường phân giác AH của góc BAC (đường này đồng thời là đường cao, đường trung trực, đường trung tuyến).
– Hình thang cân ABCD nhận đường thẳng đi qua trung điểm hai đáy HK làm trục đối xứng.
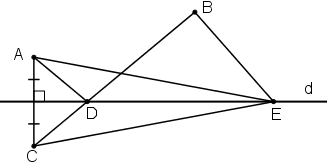
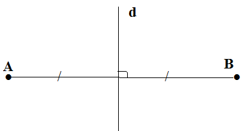
a) + A và C đối xứng qua d ⇒ d là trung trực của AC ⇒ AD = CD
⇒ AD + DB = CD + DB = CB (1)
+ E ∈ d ⇒ AE = CE ⇒ AE + EB = CE + EB (2)
+ CB < CE + EB (3)
Từ (1), (2), (3) ⇒ AD + DB < AE + EB
b) Vì với mọi E ∈ d thì AE + EB > AD + DB
Do đó con đường ngắn nhất bạn Tú nên đi là đường ADB.
- Các biển báo ở hình a, b, d có trục đối xứng.
- Biển báo c không có trục đối xứng.
a) Đúng
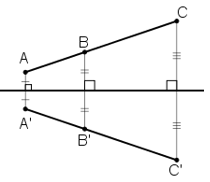
b) Đúng vì hai tam giác đối xứng nhau qua một trục thì bằng nhau nên chúng cũng có chu vi bằng nhau.
c) Đúng. Tất cả các đường thẳng đi qua tâm đều là trục đối xứng của đường tròn.
d) Sai.
Mọi đoạn thẳng AB đều có hai trục đối xứng là đường thẳng AB và đường trung trực của đoạn thẳng AB.
a) Cắt được chữ D:
Gấp đôi chữ D theo đường thẳng là trục đối xứng của chữ D như trên hình vẽ.
Một số chữ cái in hoa có trục đối xứng:
- Chỉ có một trục đối xứng dọc: A, M, T, U, V, Y
- Chỉ có một trục đối xứng ngang: B, C, D, E, K
- Có hai trục đối xứng dọc và ngang: H, I, O , X
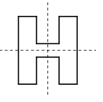
b) Có thể gấp tờ giấy làm tư để cắt chữ H vì chữ H có hai trục đối xứng vuông góc.





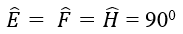
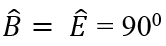
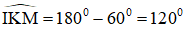
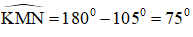
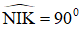
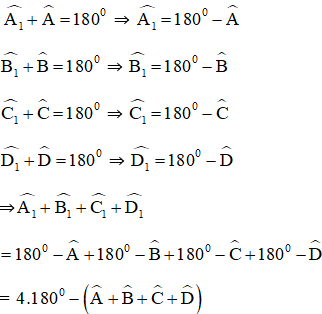
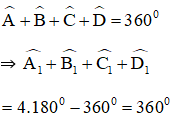
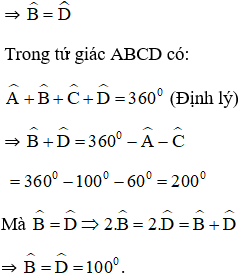








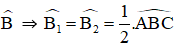
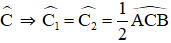
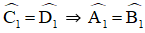






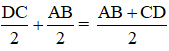



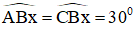

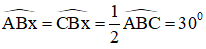
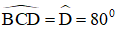
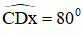
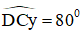






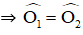
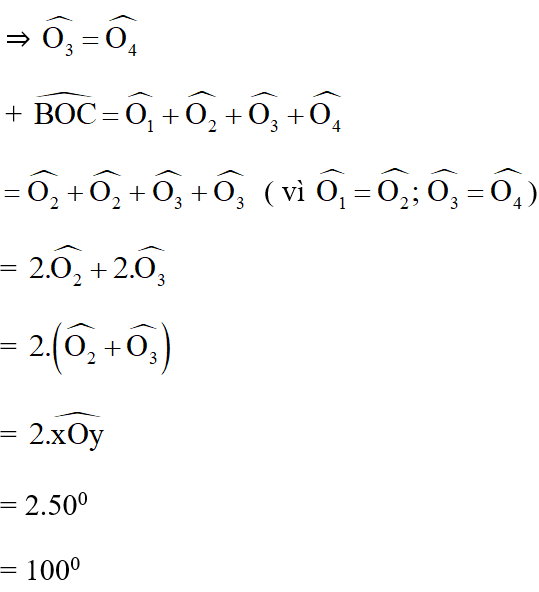


Nhận xét
Đăng nhận xét