[HH8] TỨ GIÁC - &02. Hình bình hành. Hình chữ nhật. Hình thoi. Hình vuông
Hướng dẫn giải.
- Tứ giác ABCD là hình bình hành vì có AB // CD và AB = CD = 3 (dấu hiệu nhận biết 3)
- Tứ giác EFGH là hình bình hành vì có EH // FG và EH = FG = 3 (dấu hiệu nhận biết 3)
- Tứ giác MNPQ là hình bình hành vì có MN = PQ và MQ = NP (dấu hiệu nhận biết 2)
(Chú ý:
- Với các tứ giác ABCD, EFGH còn có thể nhận biết là hình bình hành bằng dấu hiệu nhận biết 2.
- Với tứ giác MNPQ còn có thể nhận biết là hình bình hành bằng dấu hiệu nhận biết 5.)
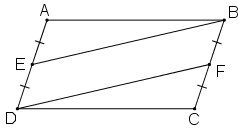
Cách 1:
+ ABCD là hình bình hành ⇒ AB = CD, AD = BC, Â = Ĉ.
+ E là trung điểm của AD ⇒ AE = AD/2
F là trung điểm của BC ⇒ CF = BC/2
Mà AD = BC (cmt) ⇒ AE = CF.
+ Xét ΔAEB và ΔCFD có: AB = CD, Â = Ĉ, AE = CF (cmt)
⇒ ΔAEB = ΔCFD (c.g.c) ⇒ EB = DF.
Cách 2:
ABCD là hình bình hành ⇒ AD//BC và AD = BC.
+ AD // BC ⇒ DE // BF
+ E là trung điểm của AD ⇒ DE = AD/2
F là trung điểm của BC ⇒ BF = BC/2
Mà AD = BC ⇒ DE = BF.
+ Tứ giác BEDF có: DE // BF và DE = BF ⇒ BEDF là hình bình hành ⇒ BE = DF.
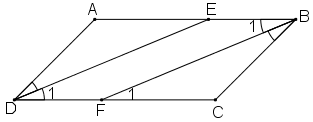
a) Ta có:
+ ABCD là hình bình hành ⇒ AB // CD ⇒ 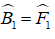
+ DE là tia phân giác của góc D

Mà hai góc này ở vị trí đồng vị ⇒ DE // BF (đpcm)
b) Tứ giác DEBF có: DE // BF (chứng minh ở câu a)
BE // DF (vì AB // CD)
⇒ DEBF là hình bình hành.
a) Đúng, vì hình thang có hai đáy song song lại có thêm hai cạnh đáy bằng nhau nên là hình bình hành theo dấu hiệu nhận biết 5
b) Đúng, vì khi đó ta được tứ giác có các cạnh đối song song là hình bình hành (định nghĩa)
c) Sai.
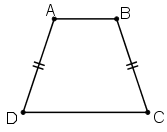
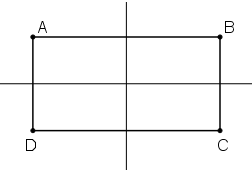
Ví dụ tứ giác ABCD ở dưới có AB = CD nhưng không phải hình bình hành.
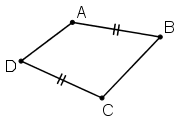
d) Sai, vì hình thang cân có hai cạnh bên bằng nhau nhưng nó không phải là hình bình hành.
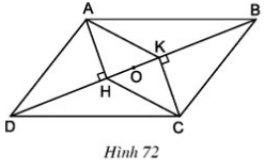
a)+ ABCD là hình bình hành ⇒ AD // BC và AD = BC.
⇒ ∠ADH = ∠CBK (Hai góc so le trong).
Hai tam giác vuông AHD và CKB có: AD = BC; ∠ADH = ∠CBK
⇒ ΔAHD = ΔCKB (cạnh huyền, góc nhọn) ⇒ AH = CK
+ AH ⊥ BD; CK ⊥ BD ⇒ AH // CK
Tứ giác AHCK có AH // CK, AH = CK nên là hình bình hành.
b) Hình bình hành AHCK có O là trung điểm HK ⇒ O = AC ∩ HK ⇒ A, C, O thẳng hàng.
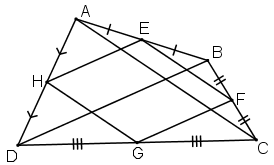
+ E là trung điểm AB, F là trung điểm BC
⇒ EF là đường trung bình của tam giác ABC ⇒ EF // AC và EF = AC/2
+ H là trung điểm AD, G là trung điểm CD
⇒ HG là đường trung bình của tam giác ACD ⇒ HG // AC và HG = AC/2.
+ Ta có: EF //AC, HG//AC ⇒ EF // HG.
EF = AC/2; HG = AC/2 ⇒ EF = HG
⇒ tứ giác EFGH là hình bình hành.
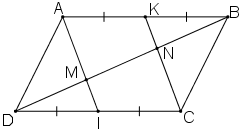
a) + K là trung điểm của AB ⇒ AK = AB/2.
+ I là trung điểm của CD ⇒ CI = CD/2.
+ ABCD là hình bình hành
⇒ AB // CD hay AK // CI và AB = CD ⇒ AB/2 = CD/2 hay AK = CI
+ Tứ giác AKCI có AK // CI và AK = CI ⇒ AKCI là hình bình hành.
b) + AKCI là hình bình hành ⇒ AI//KC hay MI//NC.
ΔDNC có: DI = IC, IM // NC ⇒ DM = MN (1)
+ AI // KC hay KN//AM
ΔBAM có: AK = KB, KN//AM ⇒ MN = NB (2)
Từ (1) và (2) suy ra DM = MN = NB.
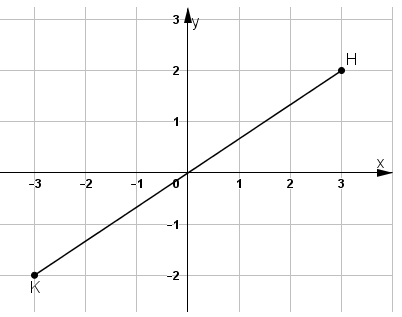
K đối xứng với H qua gốc tọa độ ⇔ O(0; 0) là trung điểm của KH.
Dựa vào hình biểu diễn ta có K(-3; -2).
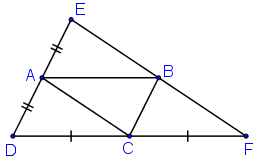
Ta có: ABCD là hình bình hành nên AB //= CD, AD//=BC.
+ E đối xứng với D qua A ⇒ AE = AD
Mà BC = AD ⇒ BC = AE.
Lại có BC // AE (vì BC // AD ≡ AE) ⇒ AEBC là hình bình hành ⇒ EB //= AC (1).
+ F đối xứng với D qua C ⇒ CF = CD
Mà AB = CD ⇒ AB = CF
Mà AB // CF (vì AB // CD ≡ CF) ⇒ ABFC là hình bình hành ⇒ AC //= BF (2)
Từ (1) và (2) suy ra E, B, F thẳng hàng và BE = BF
⇒ B là trung điểm EF ⇒ E đối xứng với F qua B
ME // AD (vì ME // AC)
Nên AEMD là hình bình hành, I là trung điểm của DE nên I cũng là trung điểm của AM, do đó A đối xứng với M qua I.
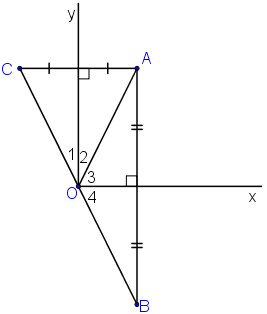
+ B đối xứng với A qua Ox ⇒ Ox là đường trung trực của AB ⇒ OA = OB (1)
+ C đối xứng với A qua Oy ⇒ Oy là đường trung trực của AC ⇒ OA = OC (2)
Từ (1) và (2) suy ra OB = OC (*).
+ Xét ΔOAC cân tại O (do OA = OC) có Oy là đường trung trực
⇒ Oy đồng thời là đường phân giác
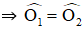
Xét ΔOAB cân tại O có Ox là đường trung trực ⇒ Ox đồng thời là đường phân giác
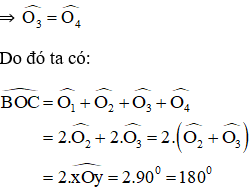
⇒ B, O, C thẳng hàng (**)
Từ (*) và (**) suy ra O là trung điểm BC ⇒ B đối xứng với C qua O.
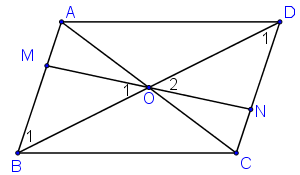
+ ABCD là hình bình hành có O là giao điểm hai đường chéo ⇒ OB = OD.
+ ABCD là hình bình hành ⇒ AB // CD ⇒ 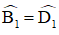
Hai tam giác BOM và DON có:
⇒ ΔBOM = ΔDON (g.c.g) ⇒ OM = ON ⇒ O là trung điểm của MN
⇒ M đối xứng với N qua O.
- Hình 83a có tâm đối xứng là trung điểm của đoạn thẳng AB
- Hình 83b không có tâm đối xứng
(Lưu ý: Trọng tâm đồng thời là trực tâm của tam giác đều ABC không phải tâm đối xứng của tam giác đó)
- Hình 83c có tâm đối xứng là tâm của hình tròn.
- Hình 83d không có tâm đối xứng.
a) Đúng, vì nếu lấy một điểm O bất kì trên đường thẳng thì nó chia đường thẳng đó thành hai và với bất kì một điểm M, trên tia này cũng luôn có một điểm M' đối xứng với nó qua O trên tia kia.
b) Sai,
Giả sử tam giác ABC có trọng tâm G.
Khi đó điểm A’ đối xứng với A qua G không nằm trong tam giác.
c) Đúng, vì hai tam giác đối xứng với nhau qua một điểm thì chúng bằng nhau.
Do đó chu vi của chúng bằng nhau.
Hướng dẫn giải.
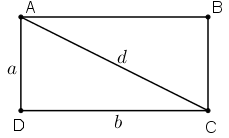
Trong hình chữ nhật ABCD ta luôn có
Do đó áp dụng định lý Py-ta-go ta có: d2 = a2 + b2.
Vậy :
- Cột thứ hai: d2 = a2 + b2 = 52 + 122 = 25 + 144 = 169 nên d = 13
- Cột thứ ba: a2 + b2 = d2 ⇒ a2 = d2 – b2 = (√10)2 – (√6)2 = 4 nên a = 2
- Cột thứ tư: a2 + b2 = d2 ⇒ b2 = d2 – a2 = 72 – (√13)2 = 36 nên b = 6.
Vậy ta có bảng sau:
| a | 5 | 2 | √13 |
| b | 12 | √6 | 6 |
| d | 13 | √10 | 7 |
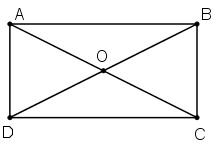
Giả sử ABCD là hình chữ nhật. Gọi O là giao điểm của AC và BD.
Theo tính chất đường chéo của hình chữ nhật ta có; hai đường chéo bằng nhau và cắt nhau tại trung điểm mỗi đường.
Vậy: OA = OC và OB= OD
Do đó, O là tâm đối xứng của hình chữ nhật đó.
b)
Áp dung tính chất: Đường thẳng đi qua trung điểm hai đáy của hình thang cân là trục đối xứng của hình thang cân đó.
ABCD là hình chữ nhật ⇒ ABCD là hình thang cân (hai đáy AB và CD)
⇒ Đường thẳng đi qua trung điểm AB và CD là trục đối xứng ABCD.
Tương tự vậy: ABCD cũng là hình thang cân với hai đáy AD và BC
⇒ Đường thẳng đi qua trung điểm AD và BC là trục đối xứng của ABCD.
Vậy ta có điều phải chứng minh.
Theo định lý Pi-ta-go ta có: a2 = 72 + 242 = 625 ⇒ a = 25cm
⇒ Độ dài trung tuyến ứng với cạnh huyền bằng: a/2 = 25/2 = 12,5 (cm).
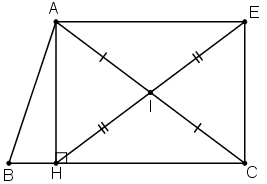
I là trung điểm của AC ⇒ IA = IC.
E đối xứng với H qua I ⇒ IE = IH ⇒ AC ∩ HE = I là trung điểm của AC và HE
⇒ AHCE là hình bình hành (dấu hiệu nhận biết 4)
Lại có : Ĥ = 90º ⇒ AHCE là hình chữ nhật (đpcm).
a) Đúng
Gọi O là trung điểm của AB.
Ta có CO là trung tuyến ứng với cạnh huyền nên ⇒ OC = AB/2 = OA = OB.
⇒ A, B, C cùng thuộc đường tròn bán kính OA.
Tâm O là trung điểm của AB nên AB là đường kính.
Vậy C thuộc đường tròn đường kính AB.
b) Đúng
Gọi O là tâm đường tròn. ⇒ OA = OB = OC = R
AB là đường kính nên AB = 2R.
Tam giác ABC có CO là trung tuyến và CO = AB/2 ⇒ ΔABC vuông tại C.
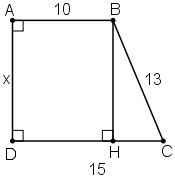
* Kẻ BH vuông góc CD.
Xét tứ giác ABHD có:
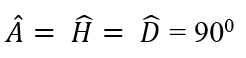
=> Tứ giác ABHD là hình chữ nhật
=> AB = DH= 10 ( hình chữ nhật có các cạnh đối bằng nhau)
+ Suy ra: HC =DC- DH =15- 10= 5
+ Áp dụng định lí py- ta- go vào tam giác vuông BHC có:
BC2 = BH2 + HC2 ⇔ 132 = BH2 + 52 ⇔ BH2 = 132 – 52 = 144 ⇔ BH = 12
+ Do ABHD là hình chữ nhật nên AD= BH = 12. Vậy x= 12

Vậy tứ giác EFGH là hình chữ nhật.
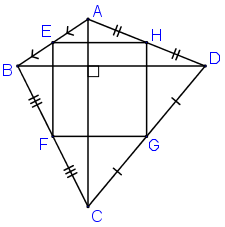
Ta có EB = EA, FB = FC (gt) ⇒ EF là đường trung bình của ΔABC
⇒EF // AC và EF = AC/2 (1)
HD = HA, GD = GC ⇒ HG là đường trung bình của ΔADC
⇒ HG // AC và HG = AC/2 (2)
Từ (1) và (2) suy ra EF // HG và EF = HG ⇒ Tứ giác EFGH là hình bình hành (*)
EA = EB, HA = HD ⇒ EH là đường trung bình của ΔABD ⇒ EH // BD.
Mà EF // AC, AC ⊥ BD ⇒ EH ⊥ EF ⇒ Ê = 90º (**)
Từ (*) và (**) suy ra EFGH là hình chữ nhật.
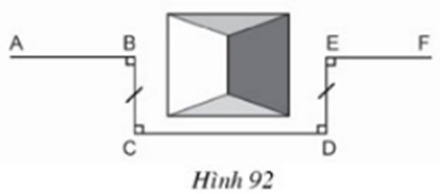
Tứ giác BCDE có: BC // DE (vì cùng vuông góc với CD); BC = DE
nên BCDE là hình bình hành ⇒ CD // BE.
Lại có : 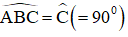
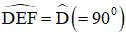
Theo tiên đề Ơ-clit suy ra A, B, E, F thẳng hàng.
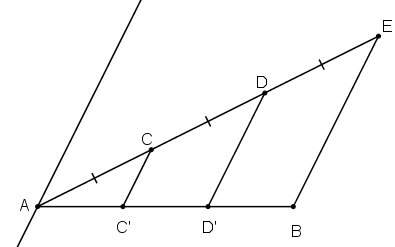
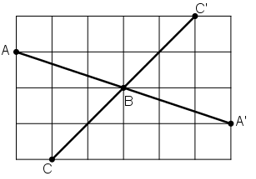
Kẻ đường thẳng At // CC’ // DD’ // BE như hình vẽ.
Ta có: AC = CD = DE ⇒ At, CC’, DD‘, BE là các đường thẳng song song cách đều
⇒ AC’ = C’D’ = D’B hay đoạn thẳng AB bị chia ra làm 3 phần bằng nhau.
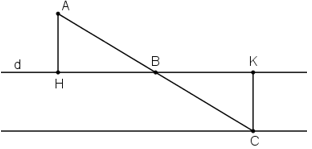
Gọi H, K là hình chiếu của A và C trên đường thẳng d.
⇒ Khoảng cách từ A đến d bằng AH ⇒ AH = 2cm.
Xét ΔAHB vuông tại H và ΔCKB vuông tại K có:
AB = BC
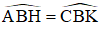
⇒ ΔAHB = ΔCKB (cạnh huyền – góc nhọn) ⇒ CK = AH = 2cm.
Vậy điểm C nằm trên đường thẳng song song với d, không đi qua A và cách d 2cm.
(1) với (7)
(2) với (5)
(3) với (8)
(4) với (6)
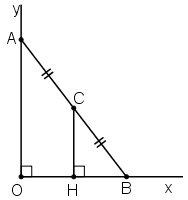
- Cách 1:
Kẻ CH ⊥ Ox.
Ta có CB = CA (gt).
CH // AO (cùng vuông góc Ox) ⇒ HB = OH
⇒ CH là đường trung bình của tam giác AOB ⇒ CH = AO/2 = 1cm.
Điểm C cách tia Ox cố định một khoảng không đổi 1cm nên C di chuyển trên tia song song với Ox, cách Ox một khoảng bằng 1cm và nằm trong góc xOy.
- Cách 2:
Vì C là trung điểm của AB nên OC là trung tuyến ứng với cạnh huyền AB do đó OC = CA.
Điểm C di chuyển trên tia Em thuộc đường trung trực của OA.
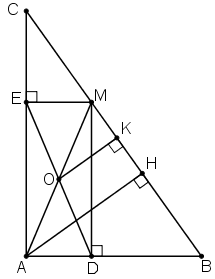
a) Tứ giác ADME có: 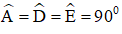
O là trung điiểm của đường chéo DE nên O cũng là trung điểm của đường chéo AM.
Vậy A, O, M thẳng hàng.
b) Kẻ AH ⊥ BC; OK ⊥ BC. Ta có OA = OM, OK // AH (cùng vuông góc BC)
⇒ MK = KH ⇒ OK là đường trung bình của ΔMAH ⇒ OK = AH/2.
⇒ điểm O cách BC một khoảng cố định bằng AH/2
⇒ O nằm trên đường thẳng song song với BC.
Mặt khác khi M trùng C thì O chính là trung điểm của AC, khi M trùng B thì O chính là trung điểm của AB.
Vậy O di chuyển trên đoạn thẳng PQ là đường trung bình của tam giác ABC.
c) Vì AH là đường cao hạ từ A đến BC nên AM ≥ AH (trong tam giác vuông thì cạnh huyền là cạnh lớn nhất).
Vậy AM nhỏ nhất khi M trùng H.
- Căn cứ vào tính chất đường thẳng song song với một đường thẳng cho trước.
- Vì điểm C cách mép gỗ AB một khoảng không đổi bằng 10cm nên khi tay di chuyển thì đầu bút chì C vạch nên một đường thẳng song song với AB và cách AB một khoảng 10cm.
Hướng dẫn giải.
– Hình 102a: ABCD là hình thoi vì có AB = BC = CD = DA
– Hình 102b: EFGH là hình thoi vì:
EF = GH và EH = FG ⇒ EFGH là hình bình hành
Lại có EG là tia phân giác của Ê ⇒ EFGH là hình bình hành. (Dấu hiêu 4).
- Hình 102c: KINM là hình thoi vì:
IKMN có hai đường chéo cắt nhau tại trung điểm mỗi đường ⇒ IKMN là hình bình hành
Lại có IM ⊥ KN ⇒ IKMN là hình thoi. (Dấu hiệu 3).
– Hình 102e: ADBC là hình thoi vì:
AC = AD = AB (C, B, D cùng thuộc đường tròn tâm A).
BC = BA = BD (A, C, D cùng thuộc đường tròn tâm B) ⇒ AC = CB = BD = DA
⇒ ACBD là hình thoi.
- Tứ giác trên hình 102d không là hình thoi vì 4 cạnh không bằng nhau.
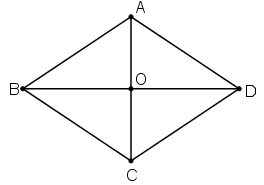
- Gọi ABCD là hình thoi, O là giao điểm hai đường chéo. ⇒ O là trung điểm của AC và BD.
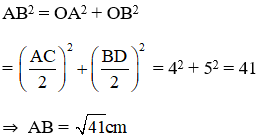
Vậy chọn đáp án là B.
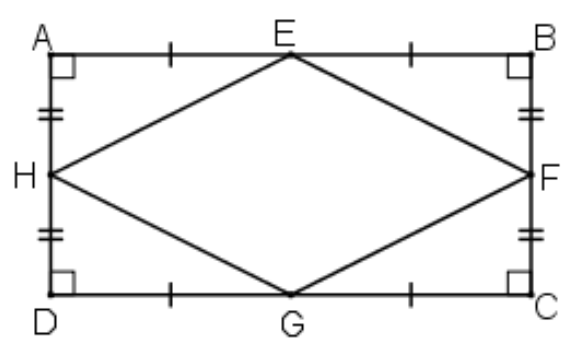
* Xét tam giác ABD có E và H lần lượt là trung điểm của AB và AD
=> EH là đường trung bình của tam giác
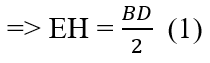
* Chứng minh tương tự, ta có:
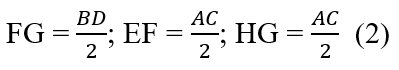
* Lại có, ABCD là hình chữ nhật nên AC = BD (3)
Từ (1), (2), (3) suy ra: EF = FG = GH= HE => tứ giác EFGH là hình thoi.
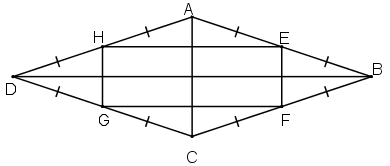
* Xét tam giác ABC có E và F lần lượt là trung điểm của AB và BC
=> EF là đường trung bình của tam giác ABC
* Tương tự tam giác ADC có HG là đường trung bình nên:
Từ (1) và (2) suy ra: EF // HG và EF = HG => tứ giác EFGH là hình bình hành.
Lại có: EF // AC và BD ⊥ AC nên BD ⊥ EF
EH // BD và EF ⊥ BD nên EF ⊥ EH
Nên
Hình bình hành EFGH có Ê = 90º nên là hình chữ nhật
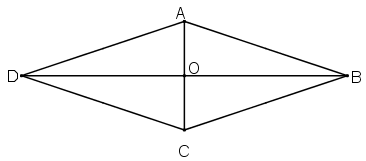
a) ABCD là hình thoi ⇒ ABCD là hình bình hành
⇒ giao điểm O của AC và BD là tâm đối xứng của ABCD.
b)
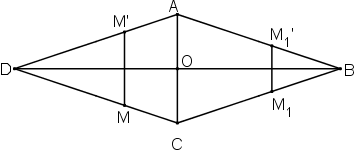
Xét hình thoi ABCD, gọi O là giao điểm của 2 đường chéo.
* Ta chứng minh: đường chéo BD là trục đối xứng của hình
Lấy điểm M bất kì thuộc hình thoi. Không mất tổng quát, M nằm trên CD.
Gọi M’ đối xứng với M qua đường thẳng BD. Ta chứng minh điểm M’ cũng thuộc hình thoi
+ Gọi I là giao điểm của MM’ và BD.
Xét tam giác DIM và DIM’ có:
DI chung ; IM= IM’ ( do M và M’ đối xứng với nhau qua BD)
=> ∆ DIM = ∆ DIM’ ( c.g.c) => DM = DM’ và
Lại có: ABCD là hình thoi nên
Từ (1) và (2) suy ra, điểm M’ nằm trên cạnh AD hay điểm M’ thuộc hình thoi
=> BD là trục đối xứng của hình thoi.
*Chứng minh tương tự, ta có: AC là trục đối xứng của hình thoi.
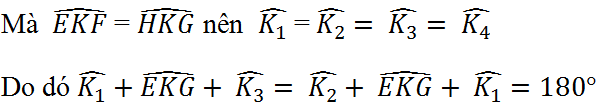
Suy ra I, K, M thẳng hàng.
Chứng minh tương tự, các điểm I, K, M, N, O cùng nằm trên một đường thẳng.
Hướng dẫn giải.
a)
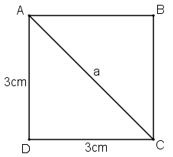
Gọi đường chéo của hình vuông có độ dài là a.
Áp dụng định lí Pi-ta-go ta có: a2 = 32 + 32 = 18 suy ra a = √18 = 3√2
Vậy đường chéo của hình vuông đó bằng 3√2 (cm)
b)
Gọi cạnh của hình vuông là a.
Áp dụng định lí Pi-ta-go ta có: a2 + a2 = 22 ⇒ 2a2 = 4 ⇒ a2 = 2 ⇒ a = √2
Vậy cạnh của hình vuông đó bằng √2 (dm).

+ Hình vuông cũng là hình bình hành nên nhận O là giao điểm của hai đường chéo là tâm đối xứng.
+ Hình vuông cũng là hình thoi nên nhận hai đường chéo AC và BD là các trục đối xứng.
+ Hình vuông cũng là hình thang cân nên nhận đường thẳng nối trung điểm các cặp cạnh đối diện là trục đối xứng.
Vậy hình vuông có 1 tâm đối xứng và 4 trục đối xứng như trên.
Cách 1:
Tứ giác AEDF có EA // DF (cùng vuông góc AF)
DE // FA (cùng vuông góc AE) ⇒ AEDF là hình bình hành (theo định nghĩa)
Hình bình hành AEDF có đường chéo AD là phân giác của góc A ⇒AEDF là hình thoi.
Hình thoi AEDF có Â = 90º ⇒ AEDF là hình vuông.
Cách 2:
Tứ giác AEDF có EA // DF (cùng vuông góc AF)
DE // FA (cùng vuông góc AE) ⇒ AEDF là hình bình hành (theo định nghĩa)
Hình bình hành AEDF có Â = 90º ⇒ AEDF là hình chữ nhật.
Hình chữ nhật AEDF có AD là phân giác của  ⇒ AEDF là hình vuông.
* Do ABCD là hình vuông nên AB = BC = CD = DA.
Theo giả thiết ta có: AE = BF = CG = DH nên ta có:
AB – AE = BC – BF = CD – CG = DA – DH ⇔ BE = CF= DG = HA
* Xét các tam giác vuông AEH, BFE, CGF, DHG có:
AE= BF = CG = DH (giả thiết)
HA= BE = CF = DG (chứng minh trên)
⇒ ΔAEH = ΔBFE = ΔCGF = ΔDHG ( c.g.c)
Suy ra: HE = EF = FG = GH (các cạnh tương ứng)
* Tứ giác EFGH là hình thoi có 1 góc bằng 90o nên EFGH là hình vuông.
- Các câu a và d sai.
- Các câu b, c, e đúng.
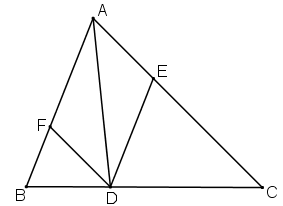
a) Tứ giác AEDF là hình bình hành.
Vì có DE // AF, DF // AE (gt) (theo định nghĩa)
b) Hình bình hành AEDF là hình thoi khi AD là tia phân giác của góc A. Vậy nếu D là giao điểm của tia phân giác góc A với cạnh BC thì AEDF là hình thoi.
c) Nếu ΔABC vuông tại A thì AEDF là hình chữ nhật (vì là hình bình hành có một góc vuông).
d) Nếu ABC vuông tại A và D là giao điểm của tia phân giác của góc A với cạnh BC thì AEDF là hình vuông (vì vừa là hình chữ nhật, vừa là hình thoi).
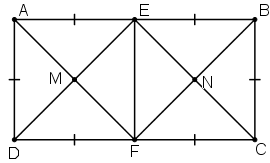
a) E, F là trung điểm AB, CD ⇒ AE = EB = AB/2, DF = FC = CD/2.
Ta có: AB = CD = 2AD = 2BC ⇒ AE = EB = BC = CF = FD = DA.
+ Tứ giác ADFE có AE // DF, AE = DF ⇒ ADFE là hình bình hành.
Hình bình hành ADFE có Â = 90º ⇒ ADFE là hình chữ nhật.
Hình chữ nhật ADFE là hình chữ nhật có AE= AD ⇒ ADFE là hình vuông.
b) Tứ giác DEBF có EB // DF, EB = DF nên là hình bình hành
Do đó DE // BF
Tương tự: AF // EC
Suy ra EMFN là hình bình hành
Theo câu a, ADFE là hình vuông nên ME = MF, ME ⊥ MF.
Hình bình hành EMFN có M̂ = 90º nên là hình chữ nhật.
Lại có ME = MF nên EMFN là hình vuông.
- Tứ giác nhận được theo nhát cắt của AB là hình thoi vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường và vuông góc với nhau.
- Nếu có thêm OA = OB thì hình thoi nhận được có hai đường chéo bằng nhau nên là hình vuông.
Hướng dẫn giải.
a) Tập hợp các hình chữ nhật là tập hợp con của tập hợp các hình bình hành, hình thang.
b) Tập hợp các hình thoi là tập hợp con của tập hợp các hình bình hành, hình thang.
c) Giao của tập hợp các hình chữ nhật và tập hợp các hình thoi là tập hợp các hình vuông.
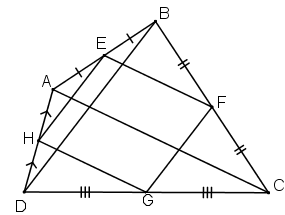
Ta có: EB = EA, FB = FC (gt) ⇒ EF là đường trung bình của ΔABC ⇒ EF // AC và EF = AC/2.
Ta có: HA = HD, GC = GD ⇒ HG là đường trung bình của ΔADC ⇒ HG // AC và HG = AC/2.
Do đó EF // HG, EF = HG ⇒ EFGH là hình bình hành.
a) Hình bình hành EFGH là hình chữ nhật ⇔ EH ⊥ EF ⇔ AC ⊥ BD (vì EH // BD, EF// AC)
b) Hình bình hành EFGH là hình thoi ⇔ EF = EH
⇔ AC = BD (Vì EF = AC/2, EH = BD/2)
c) EFGH là hình vuông ⇔ EFGH là hình thoi và EFGH là hình chữ nhật
⇔ AC = BD và AC ⊥ DB.
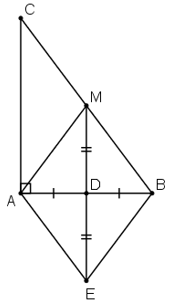
a) Ta có MB = MC, DB = DA ⇒ MD là đường trung bình của ΔABC ⇒ MD // AC
Mà AC ⊥ AB ⇒ MD ⊥ AB.
Mà D là trung điểm ME ⇒ AB là đường trung trực của ME ⇒ E đối xứng với M qua AB.
b) + MD là đường trung bình của ΔABC ⇒ AC = 2MD.
E đối xứng với M qua D ⇒ D là trung điểm EM ⇒ EM = 2.MD ⇒ AC = EM.
Lại có AC // EM ⇒ Tứ giác AEMC là hình bình hành.
+ Tứ giác AEBM là hình bình hành vì có các đường chéo cắt nhau tại trung điểm của mỗi đường.
Hình bình hành AEBM lại có AB ⊥ EM nên là hình thoi.
c) Ta có: BC = 4cm ⇒ BM = 2cm
Chu vi hình thoi AEBM bằng 4.BM = 4.2 = 8cm
d)- Cách 1:
Hình thoi AEBM là hình vuông ⇔ AB = EM ⇔ AB = AC
Vậy nếu ABC vuông có thêm điều kiện AB = AC (tức tam giác ABC vuông cân tại A) thì AEBM là hình vuông.
- Cách 2:
Hình thoi AEBM là hình vuông ⇔ AM ⊥ BM ⇔ ΔABC có trung tuyến AM là đường cao
⇔ ΔABC cân tại A.
Vậy nếu ΔABC vuông có thêm điều kiện cân tại A thì AEBM là hình vuông.
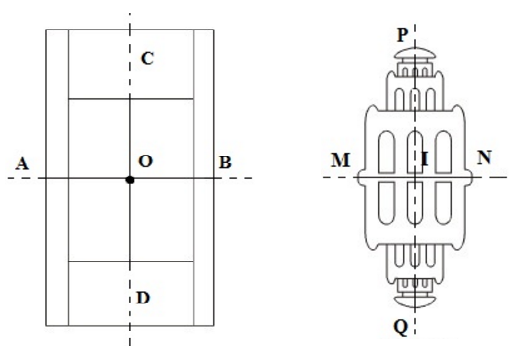
a) Hình 110
- Hai trục đối xứng AB và CD.
- Một tâm đối xứng là O.
b) Hình 111
- Hai trục đối xứng là MN và PQ
- Một tâm đối xứng là I.














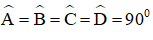



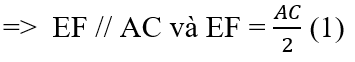
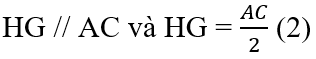
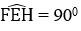
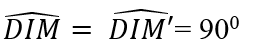
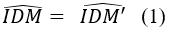
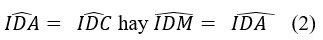









Nhận xét
Đăng nhận xét