[HH7] Hình học phẳng - &01. Từ song song đến vuông góc
Hướng dẫn giải.
a) Góc xOy và góc x'Oy' là hai góc đối đỉnh vì cạnh Ox là tia đối của cạnh Ox' và cạnh Oy là tia đối của cạnh Oy'.
b) Góc x'Oy và góc xOy' là hai góc đối đỉnh vì cạnh Ox' là tia đối của cạnh Ox và cạnh Oy là tia đối của cạnh Oy'.
a) Hai góc có mỗi cạnh của góc này là tia đối của một cạnh của góc kia được gọi là hai góc đối đỉnh.
b) Hai đường thẳng cắt nhau tạo thành hai cặp góc đối đỉnh.
Cặp góc đối đỉnh thứ nhất là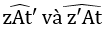 
(vì Az và Az’; At’ và At là các cặp tia đối nhau).
Cặp góc đối đỉnh thứ hai là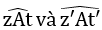 
(vì Az và Az’; At và At’ là các cặp tia đối nhau)
Vẽ tia By’ là tia đối của tia By
Vẽ tia Bx’ là tia đối của tia Bx
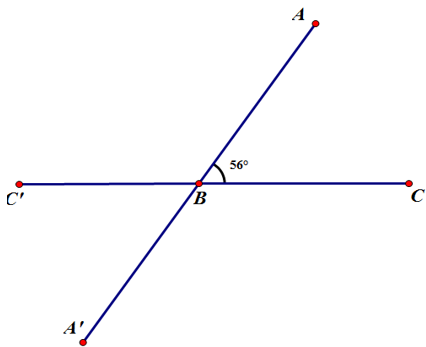
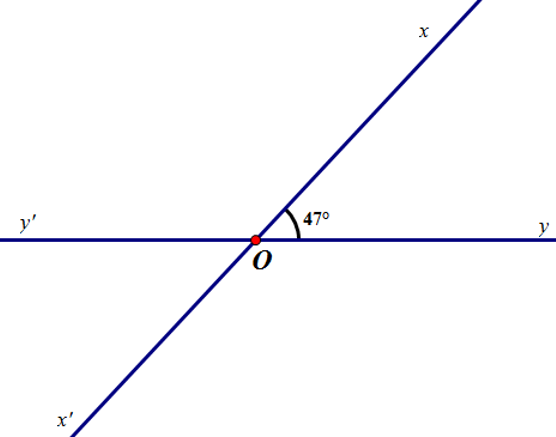
Vẽ đường thẳng xx’.
Trên đường thẳng xx’ ta lấy điểm O bất kì.
Sử dụng thước đo góc để vẽ tia yy’ đi qua O sao cho góc xOy = 47º.
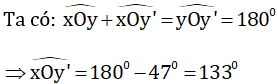
Nhận xét: Ox là tia đối của tia Ox’; Oy là tia đối của tia Oy’ suy ra:
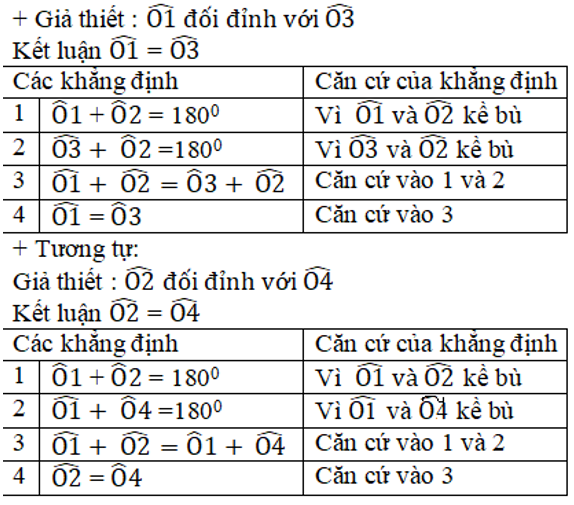
+ hai góc xOy và x’Oy’ là hai góc đối đỉnh nên 
+ hai góc xOy’ và x’Oy là hai góc đối đỉnh nên 
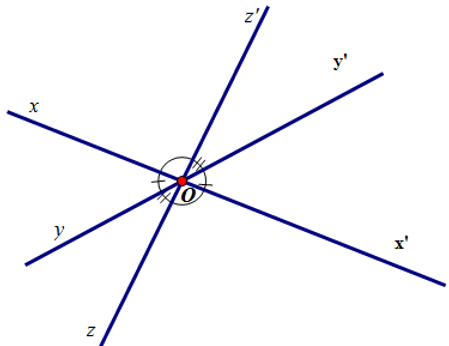
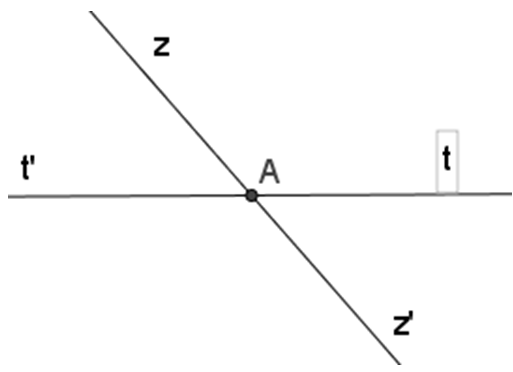
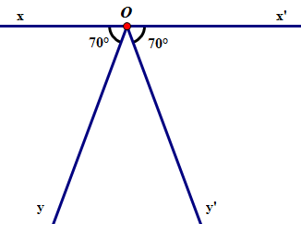
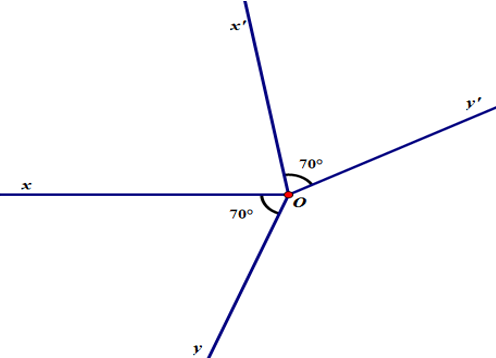
Trên hình vẽ ba đường thẳng xx', yy', zz' cùng đi qua điểm O.
Tên các cặp góc bằng nhau là:
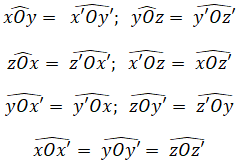
Cách 1: Vẽ đường thằng x’x . Trên x’x lấy điểm O
Vẽ góc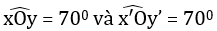 
(Oy và Oy’ cùng thuộc một nửa mặt phẳng bờ xx’).
Cách 2 : Hoặc vẽ góc 
Từ O vẽ tia Ox’ bất kì (không phải là tia đối của Ox )
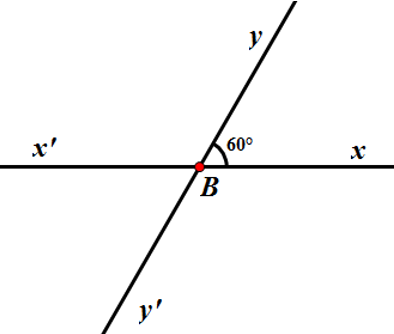
Hai góc vuông không đối đỉnh là:
+ Góc xAy và góc x’Ay.
+ Góc x’Ay và góc x’Ay’
+ Góc x’Ay’ và góc xAy’
+ Góc xAy’ và góc xAy.
a) Hai đường thẳng vuông góc với nhau là hai đường thẳng cắt nhau tạo thành một góc vuông.
b) Hai đường thẳng a và a' vuông góc với nhau được kí hiệu là a ⊥ a'.
c) Cho trước một điểm A và một đường thằng d. Có một và chỉ một đường thẳng d' đi qua A và vuông góc với d.
a) Đúng
b) Sai
Hình dưới minh họa hai đường thẳng a và b cắt nhau tại O nhưng a không vuông góc với b. Đây là một phần ví dụ bác bỏ câu: "Hai đường thẳng cắt nhau thì vuông góc"
- Phương pháp giải :
Dựa vào định nghĩa đường trung trực của đoạn thẳng :
Đường thẳng vuông góc với một đoạn thẳng tại trung điểm của nó được gọi là đường trung trực của đoạn thẳng ấy
- Đáp án :
Gấp tờ giấy sao cho điểm A trùng với điểm B .
Khi đó nếp giấy gấp sẽ trùng với đường trung trực của đoạn thẳng AB
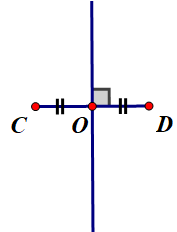
- Dùng thước có chia khoảng vẽ đoạn thẳng CD=3cm. Vẽ trung điểm O của CD bằng cách lấy O sao cho CO =1,5cm
- Dùng eke vẽ đường thẳng d vuông góc với CD tại O
- Đường thẳng d chính là đường trung trực của CD.
- Dùng eke vẽ đường thẳng d vuông góc với CD tại I. Đường thẳng d chính là đường trung trực của CD
- Nếp gấp zt vuông góc với đường thẳng xy tại O. Có bốn góc vuông là góc xOz, yOz, yOt, tOx.
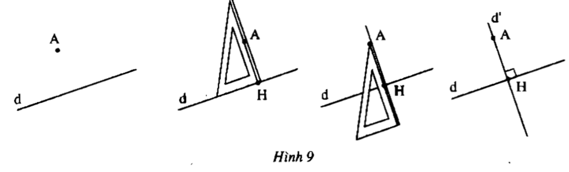
Thứ tự vẽ đường thẳng d' và d' ⊥ d như sau (hình vẽ):
- Đặt eke sao cho một mép góc vuông của eke đi qua điểm A mép góc vuông kia của eke nằm trên đoạn thẳng d
- Kẻ đoạn thẳng theo mép góc vuông của eke đi qua điểm A
- Dùng eke kéo dài đoạn thẳng trên về hai phía thành đường thẳng d' vuông góc với d
a) a và a’ không vuông góc với nhau
b) a và a’ vuông góc với nhau
c) a và a’ vuông góc với nhau
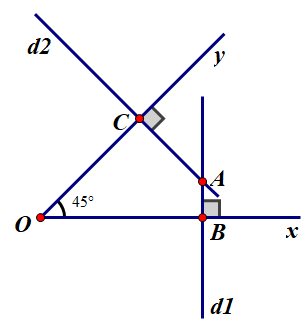
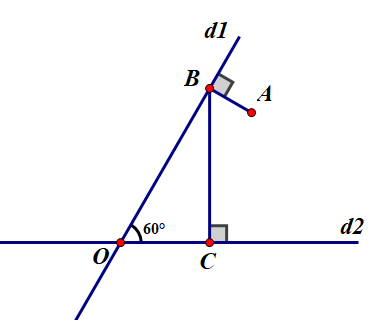
Có thể vẽ hình đã cho theo nhiều trình tự khác nhau. Ví dụ:
Trình tự 1:
Vẽ đường thẳng d2 bất kì. Lấy điểm O nằm trên d2.
Vẽ đường thẳng d1 cắt d2 tại O và tạo với d2 góc 60º.
Lấy điểm A tùy ý nằm trong 
Vẽ đoạn thẳng AB vuông góc với d1 tại B
Vẽ đoạn thẳng BC vuông góc với d2 tại C.
Trình tự 2:
Vẽ hai đường thẳng d1 ,d2 cắt nhau tại O và tạo thành góc 60º
Lấy điểm B tùy ý nằm trên tia Od1
Vẽ đoạn thẳng BC vuông góc với tia Od2 điểm C nằm trên tia Od2
Vẽ đoạn thẳng BA vuông góc với tia Od1 điểm A nằm trong góc
- Trường hợp: ba điểm A, B, C thẳng hàng
- Trường hợp: ba điểm A, B, C không thẳng hàng
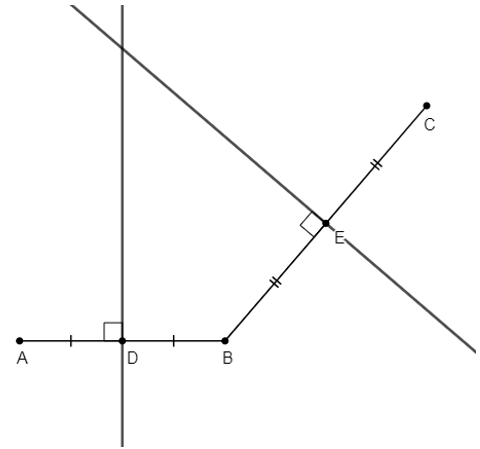
Hướng dẫn giải.
a) ... so le trong.
b) ... đồng vị.
c) ... đồng vị.
d) ... cặp góc so le trong.
a) Vẽ lại hình 15
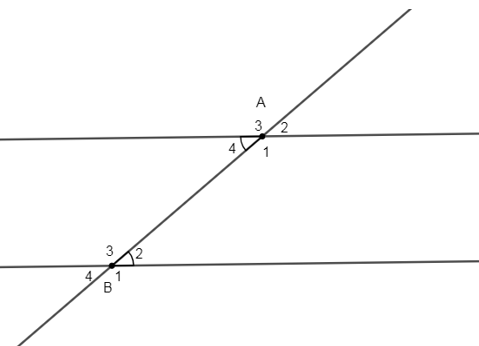
b)
(theo tính chất hai góc đối đỉnh)
(theo tính chất hai góc đối đỉnh)
(Tính chất hai góc đối đỉnh).
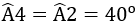
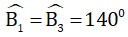
a) ... a // b.
b) ... a song song với b.
Dùng eke vẽ đường thẳng c vuông góc với đường thẳng a tại A.
Vẽ đường thẳng b đi qua B và vuông góc với c.
Khi đó ta được đường thẳng b đi qua B và song song với đường thẳng a.
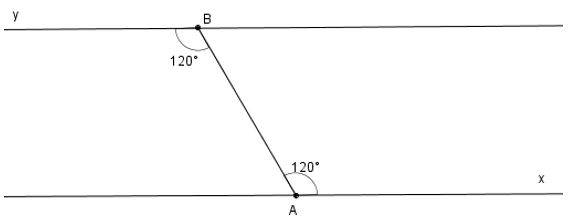
Ta có AB cắt hai đường thẳng Ax và By
Có một cặp góc so le trong bằng nhau: góc xAB = góc yBA = 120º
Vậy Ax // By (theo dấu hiệu nhận biết hai đường thẳng song song).
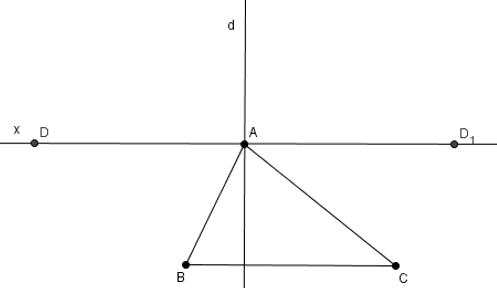
Cách vẽ:
- Vẽ đường thẳng d qua A và vuông góc với BC.
- Vẽ đường thẳng Ax vuông góc với đường thẳng d tại A. Khi đó ta có được đường thẳng Ax song song với BC (hai cặp góc so le trong tạo thành đều là góc vuông).
- Trên đường thẳng Ax đặt đoạn thẳng AD có độ dài bằng độ dài đoạn thẳng BC. Ta được đoạn AD cần vẽ (có 2 điểm D thỏa mãn).
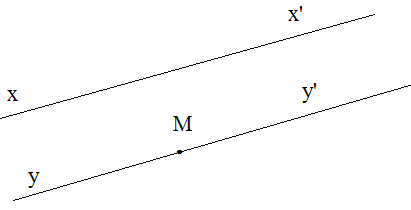
Cách vẽ:
- Vẽ một đường thẳng xx’ bất kì.
- Lấy điểm M tùy ý nằm ngoài đường thẳng xx’.
- Vẽ qua M đường thẳng yy’ sao cho yy’ //xx’
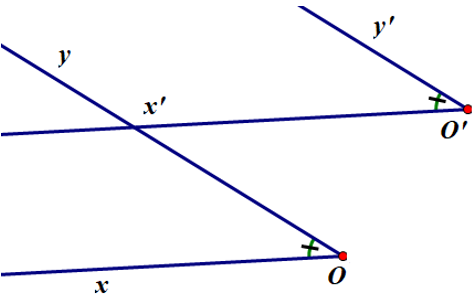
- Từ O’ vẽ O’x’ // Ox
- Từ O’ vẽ O’y’//Oy sao cho góc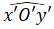 
là góc nhọn.
Ta được trường hợp hình vẽ trên
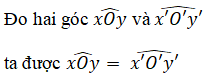
- Theo hình vẽ thì m // n, p // q
- Cách kiểm tra: Vẽ một đường thẳng tùy ý cắt p, q. Đo hai góc đồng vị hoặc góc so le trong tạo thành xem có bằng nhau không. Nếu hai góc bằng nhau thì hai đường thẳng p và q song song, còn nếu hai góc không bằng nhau thì hai đường thẳng p và q không song song.
Bài 31. Vẽ rất đơn giản, các bạn kẻ theo dòng kẻ trong vở.
a) Đúng
b) Đúng
c) Sai vì có rất nhiều đường thẳng cùng song song với đường thẳng a.
d) Sai vì qua điểm M nằm ngoài đường thẳng a chỉ có duy nhất một đường thẳng song song với a.
a) ... bằng nhau.
b)... bằng nhau.
c)... bù nhau.
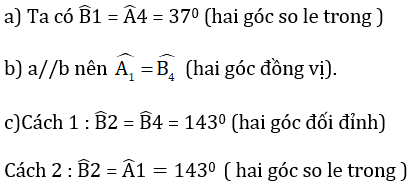
•Biết d//d’ thì suy ra
•Nếu một đường thẳng cắt hai đường thẳng song song thì : a)Hai góc so le trong bằng nhau b)Hai góc đồng vị bằng nhau c)Hai góc trong cùng phía bù nhau |
Thì suy ra d//d’ •Nếu một đường thẳng cắt hai đường thẳng Mà a) Hai góc so le trong bằng nhau Hoặc b) Hai góc đồng vị bằng nhau Hoặc c) Hai góc trong cùng phía bù nhau thì hai đường thẳng đó song song với nhau |
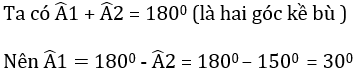
Góc nhọn tạo bởi a và d2 bằng với góc A1 (là hai góc so le trong ) nên góc đó bằng 30o
Hướng dẫn giải.
Nếu a ⊥ c và b ⊥ c thì a // b
Nếu a // b và c ⊥ a thì c ⊥ b
a) Vẽ c ⊥ a
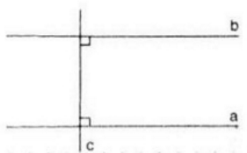
b) Vẽ b ⊥ c (như hình trên)
Ta được a song song với b vì c cắt a và b trong các góc tạo thành có 1 cặp góc so le trong bằng nhau bằng 90o
c) Phát biểu: Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau.
a) Vẽ c ⊥ a
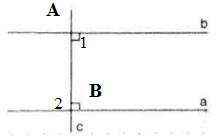
b) Vẽ b // a (hình vẽ)
- Ta được c có vuông góc với b vì a // b nên nếu c cắt a tại B thì c cũng cắt b tại A.
Vì góc A1 = 90o nên góc so le trong của nó là góc B2 = 90o ⇒ c ⊥ b
c) Phát biểu: Một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng vuông góc với đường thẳng kia.
a) Vẽ a // b
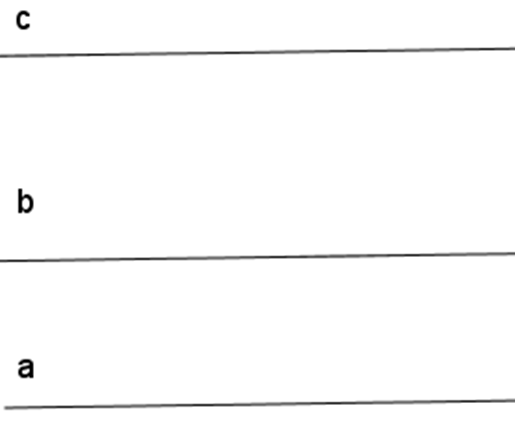
b) Vẽ c // a (hình vẽ)
- c có song song với b.
Giả sử b không song song với c thì b cắt c tại một điểm O nào đó. Khi đó qua O ta có thể vẽ được hai đường thẳng b và c cùng song song với a. Điều đó trái với tiên đề Ơ-clit về đường thẳng song song. Vậy c // b.
c) Phát biểu: Hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba thì chúng song song với nhau.
a) Vẽ d//d' và d''//d
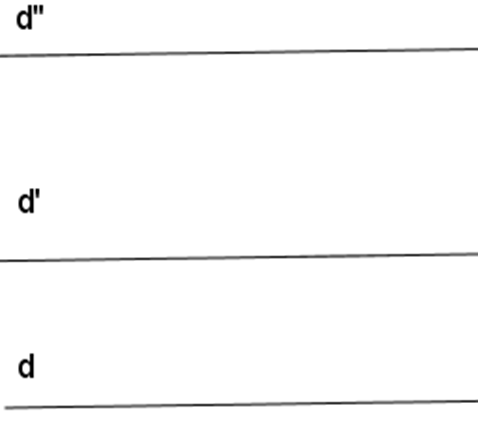
b) Suy ra d'//d'' vì
- Nếu d' cắt d'' tại điểm M thì M không nằm trên d vì d//d', d//d''
- Qua điểm M nằm ngoài d ta vẽ được hai đường thẳng d', d'' cùng song song với d. Điều này trái với tiên đề Oclit về đường thẳng song song
- Nên d' và d'' không thể cắt nhau. Vậy d'//d''
a) a//b vì a và b cùng vuông góc với đường thẳng AB.
b) Ta có:
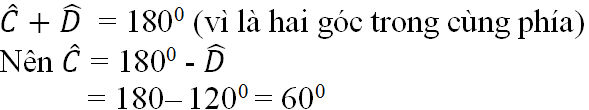
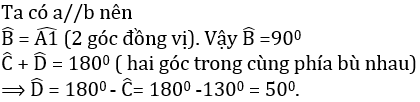
Vậy các nếp gấp là hình ảnh của một đường thẳng vuông góc với hai đường thẳng song song .
a) Giả thiết: Đường thẳng cắt hai đường thẳng sao cho có một góc so le trong bằng nhau.
Kết luận: Hai đường thẳng đó song song.
b) Giả thiết: Một đường thẳng cắt hai đường thẳng song song.
Kết luận: Hai góc so le trong bằng nhau.
a) Nếu hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ b thì song song với nhau.
b) Hình minh họa và viết giả thiết kết luận bằng kí hiệu:
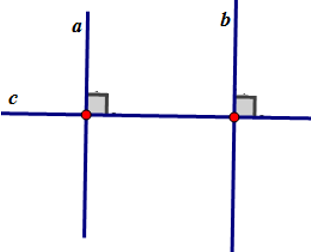
Giả thiết: a⊥c, b⊥c
Kết luận: a//b
a) Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng vuông góc với đường thẳng kia.
b) Hình minh hoa và viết giả thiết kết luận bằng kí hiệu:
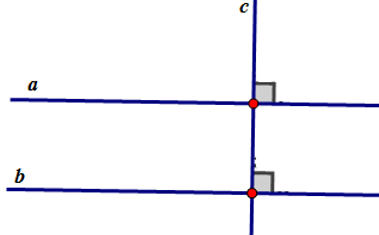
GT : a//b , c⊥a
KL : c⊥b
a) Vẽ hình:
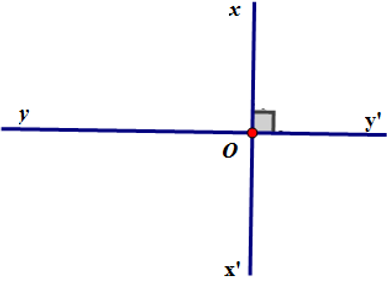
b) Viết giả thiết và kết luận:
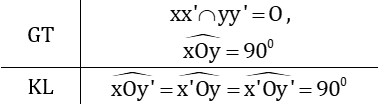
c) Điền vào chỗ trống:
Bốn cặp đường thẳng song song là: d4 // d5; d4 // d7; d5 // d7; d2 // d8
Từ hình vẽ ta có:
a) g ⊥ d; h ⊥ d
b) a // e; b // e
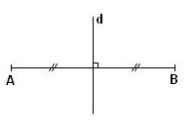
Qua I vẽ đường thẳng d vuông góc với AB
d là đường trung trực của AB
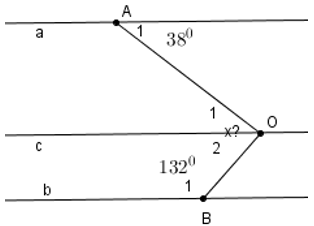
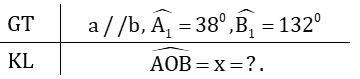
- Vẽ đường thẳng c//a đi qua O. Vì a//b và a//c nên c//b.
- a//c nên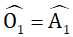 
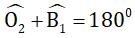
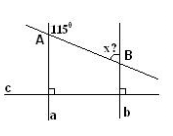
(hai góc so le trong) nên 
- b//c nên 
(hai góc trong cùng phía) nên 
Kí hiệu như hình vẽ ta có:
a ⊥ c, b ⊥ c nên suy ra a // b
Do đó x + 115o = 180o (hai góc trong cùng phía)
Nên x = 180o - 115o = 65o
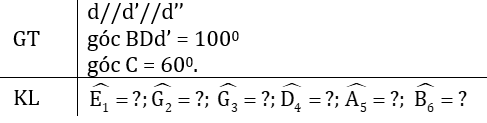
a) Nếu hai đường thằng cùng vuông góc với một đường thẳng thứ ba thì hai đường thẳng đó song song với nhau.
Hoặc: Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó sẽ vuông góc với đường thẳng còn lại .
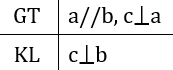
b) Nếu hai đường thẳng cùng song song với một đường thẳng thứ ba thì hai đường thẳng đó song song với nhau.
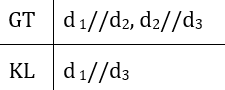
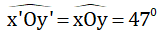
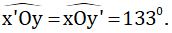
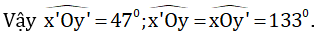
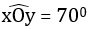
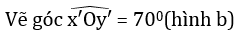
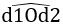
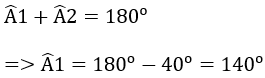
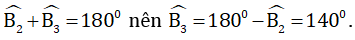
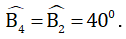
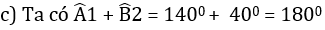
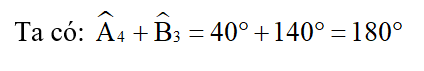
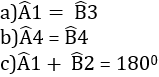
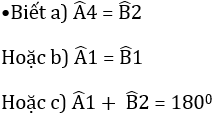
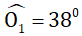
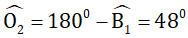
Nhận xét
Đăng nhận xét