[HH7] Hình học phẳng - &01. Tam giác và các vấn đề liên quan
Hướng dẫn giải.
- Hình 47
x + 90o + 55o = 180o
x = 180o - 90o - 55o
x = 35o
- Hình 48
x + 30o + 40o = 180o
x = 180o - 30o - 40o
x = 110o
- Hình 49
x + x + 50o = 180o
2x = 180o - 50o
x = 65o
Áp dụng định lý góc ngoài của tam giác ta có:
- Hình 50
y = 60o + 40o
y = 100o
x + 40o = 180o (2 góc kề bù)
x = 140o
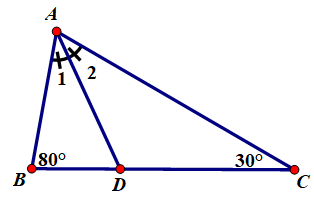
- Hình 51
Áp dụng định lý góc ngoài trong tam giác ABD có: x = 70º + 40º = 110º
Áp dụng định lý tổng ba góc trong tam giác ADC có:
y + 110º + 40º = 180º ⇒ y = 30º.

Áp dụng định lý góc ngoài trong các tam giác ABD và ACD ta có:
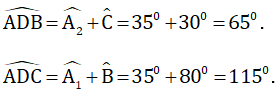

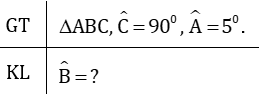
Áp dụng định lý tổng ba góc trong một tam giác ta có:
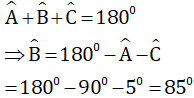
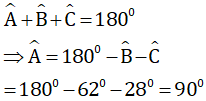
Vậy tam giác ABC là tam giác vuông.
Xét tam giác DEF có:
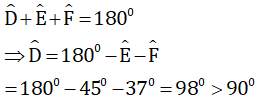
Vậy tam giác DEF là tam giác tù.
Xét tam giác HIK:
Nhận thấy
Vậy tam giác HIK là tam giác nhọn.
+ Hình 55:

+ Hình 56:

+ Hình 57 :
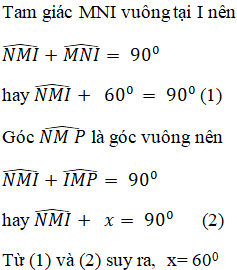
+ Hình 58:
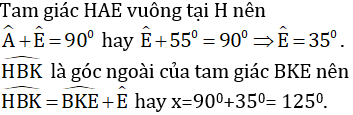
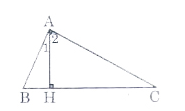
a) Tam giác ABC vuông tại A nên
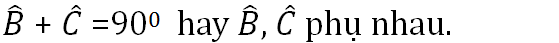
Tam giác AHB vuông tại H nên
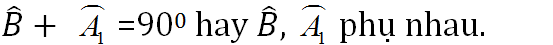
Tam giác AHC vuông tại H nên
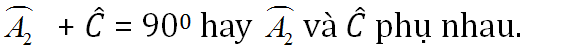
b) Ta có:
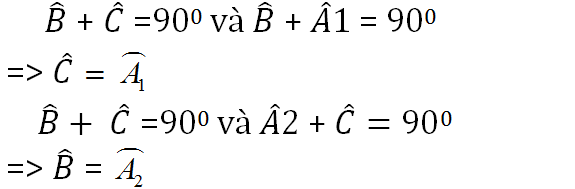
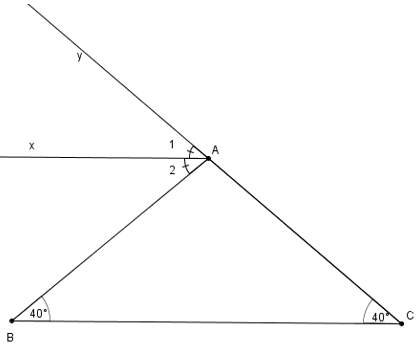
Gọi góc BAy là góc ngoài của tam giác ABC

Mà hai góc này ở vị trí so le trong nên Ax//BC (đpcm).
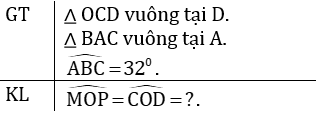
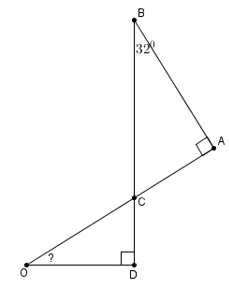
Ta có tam giác ABC vuông ở A nên
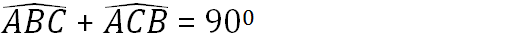
Tam giác OCD vuông ở D nên
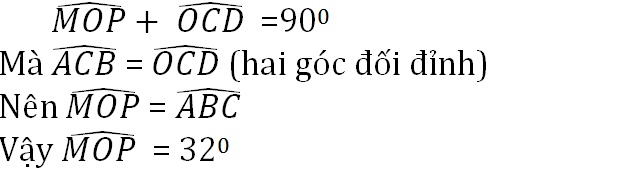
Hướng dẫn giải.
- Xem hình 63)
Ta có:
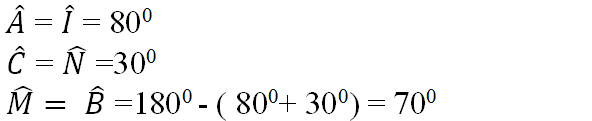
Và AB = MI; AC = IN; BC = MN
Nên ΔABC = ΔIMN
- Xem hình 64)
ΔPQR có:
Và QH = RP, HR = PQ, QR cạnh chung
Nên ΔHQR = ΔPRQ
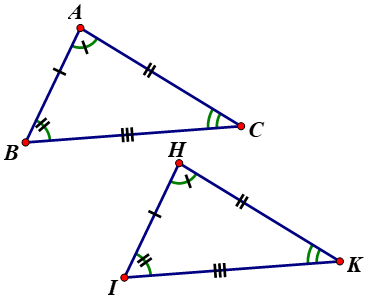
a) Vì tam giác ABC = tam giác HIK nên
- Cạnh tương ứng với cạnh BC là IK
- Góc tương ứng với góc H là góc A
b) - Các cạnh bằng nhau là: AB = HI, AC = HK, BC = IK
- Các góc bằng nhau là:
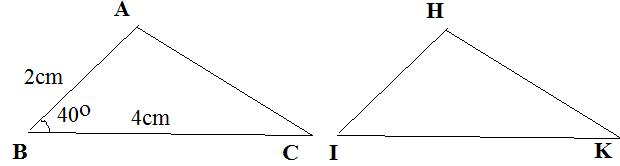
Ta có ΔABC = ΔHIK
Theo định nghĩa hai tam giác bằng nhau
HI = AB = 2cm
IK = BC = 4cm
góc I = góc B = 40º
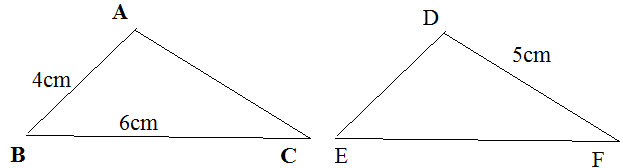
Vì ΔABC = ΔDEF nên suy ra:
AB = DE = 4cm
BC = EF = 6cm
DF = AC = 5cm
Chu vi tam giác ABC bằng:
AB + BC + CA = 4 + 6 + 5 = 15 (cm)
Chu vi tam giác DEF bằng:
DE + EF + DF = 4 + 6 + 5 = 15 (cm)

Ta có:
góc B = góc K nên B, K là hai đỉnh tương ứng
AB = KI nên A, I là hai đỉnh tương ứng
Nên ΔABC = ΔIKH
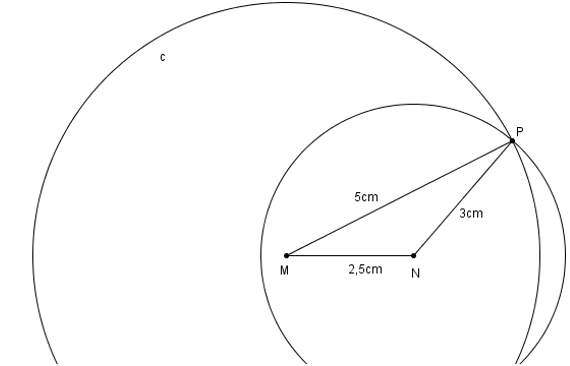
- Vẽ đoạn thẳng MN = 2,5cm.
- Trên cùng một nửa mặt phẳng bờ MN vẽ cung tròn tâm M bán kính 5cm, và cung tròn tâm N bán kính 3cm
- Hai cung tròn cắt nhau tại P. Vẽ các đoạn thẳng MP, NP ta được tam giác MNP.
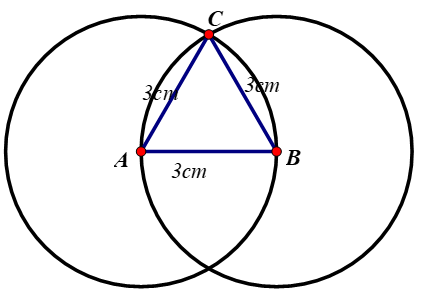
Vẽ tam giác ABC (tương tự với cách vẽ ở Bài 15):
- Vẽ cạnh AB có độ dài bằng 3 cm.
- Trên một nửa mặt phẳng bờ AB lần lượt vẽ hai cung tròn tại A và B có bán kính 3 cm
- Hai cung tròn này cắt nhau tại C. Nối các điểm A, B, C ta được tam giác ABC cần vẽ.
Đo mỗi góc của tam giác ABC ta được: góc A = góc B = góc C = 60º
- Hình 68
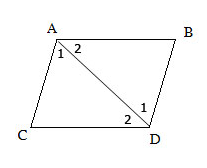
Xét tam giác ABC và tam giác ABD có:
AB = AB (cạnh chung)
AC = AD (gt)
BC = BD (gt)
Vậy ΔABC = ΔABD (c.c.c)
- Hình 69
Xét tam giác MNQ và tam giác QPM có:
MN = QP (gt)
NQ = PM (gt)
MQ cạnh chung
Vậy ΔMNQ = ΔQPM (c.c.c)
- Hình 70
Xét tam giác EHI và tam giác IKE có:
EH = IK (gt)
HI = KE (gt)
EI = IE (cạnh chung)
Vậy ΔEHI = ΔIKE (c.c.c)
Xét tam giác EHK và tam giác IKH có:
EH = IK (gt)
EK = IH (gt)
HK = KH (cạnh chung)
Vậy ΔEHK = ΔIKH (c.c.c)
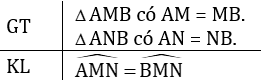
2) Thứ tự sắp xếp là d-b-a-c

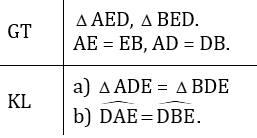
a) ΔADE và ΔBDE có:
DE cạnh chung
AD = BD (gt)
AE = BE (gt)
Vậy ΔADE = ΔBDE (c.c.c)
b) Từ ΔADE = ΔBDE (cmt) suy ra góc DAE = góc DBE (hai góc tương ứng ).
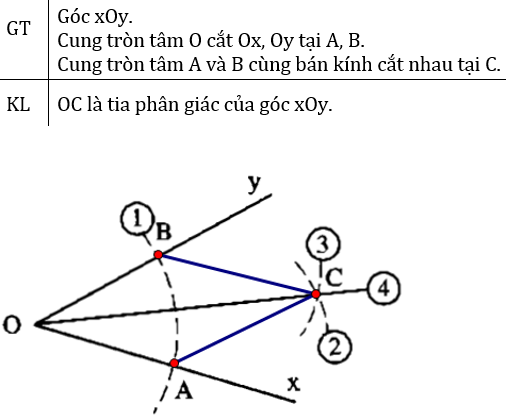
Nối BC, AC
ΔOBC và ΔOAC có:
OB = OA (bán kính)
AC = BC (gt)
OC cạnh chung
Nên ΔOBC = ΔOAC (c.c.c)
nên OC là tia phân giác của góc xOy.
Vẽ cung tròn tâm A cung này cắt tia AB ,AC theo thứ tự ở M,N
Vẽ các cung tròn tâm M và tâm N có cùng bán kính sao cho chúng cắt nhau ở điểm I.
Nối AI, ta được AI là tia phân giác của góc A.
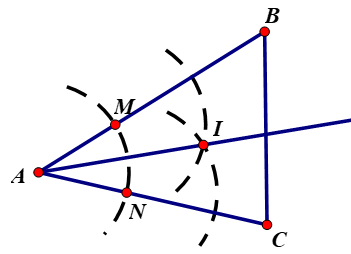
- Tương tự cho cách vẽ tia phân giác của góc B, C
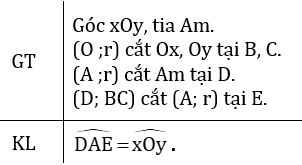
Kí hiệu: (O ;r) là đường tròn tâm O bán kính r.
B, C thuộc (O; r) nên OB = OC = r.
D thuộc (A;r) nên AD = r.
E thuộc (D; BC) và (A;r) nên AE = r, DE = BC.
Xét OBC và ADE có:
OB = AD (cùng bằng r)
OC = AE (cùng bằng r)
BC = DE
Nên ΔOBC = ΔADE (c.c.c)
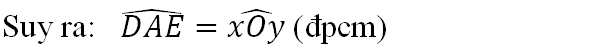

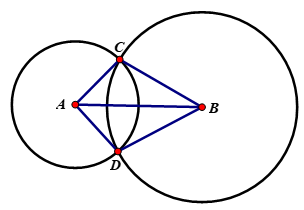
Nối BC, BD, AC, AD.
ΔABC và ΔABD có:
AC = AD (=2cm)
BC = BD (=3cm)
AB cạnh chung
Nên ΔABC = ΔABD (c.c.c)
Suy ra góc CAB = góc DAB (góc tương ứng)
⇒ AB là tia phân giác của góc CAD
Hướng dẫn giải.
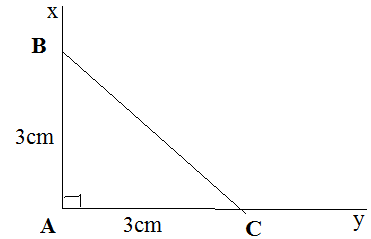
- Cách vẽ:
+ Vẽ góc xAy = 90o
+ Trên tia Ax vẽ đoạn thẳng AB = 3cm
+ Trên tia Ay vẽ đoạn thẳng AC = 3cm
+ Vẽ đoạn thẳng BC
Ta được tam giác ABC là tam giác cần vẽ
- Đo các góc B và C ta được góc B = góc C = 45º
+ Hình 82: ∆ADB = ∆ADE (c.g.c) vì :
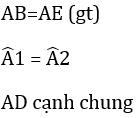
+ Hình 83: ∆HGK = ∆IKG (c.g.c) vì:
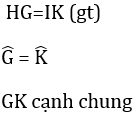
+ Hình 84: ∆PMQ và ∆PMN có:
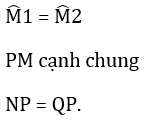
Nhưng góc M không phải góc xen giữa nên ∆PMQ không bằng ∆PMN
- Thứ tự sắp xếp là 5, 1, 2, 4, 3
Tam giác AMB và tam giác EMC có
MB = MC (gt)
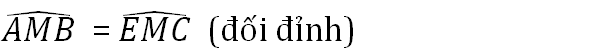
MA = ME (gt)
Do đó ΔAMB = ΔEMC (c.g.c)

a) Bổ sung thêm góc BAC = góc DAC.
b) Bổ sung thêm MA = ME.
c) Bổ sung thêm AC = BD.
- Trong ΔDEK có:
- Xét ΔABC và ΔKDE có:
AB = KD (gt)
BC = DE (gt)
Do đó ΔABC = ΔKDE
- Xét ΔMNP và ΔABC có:
MN = AB
NP = BC
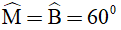
⇒ ΔMNP không bằng ΔABC
⇒ ΔMNP cũng không bằng ΔKDE.
Ta có: AB = AD, BE = DC ⇒ AB + BE = AD + DC hay AE = AC.
Xét ΔABC và Δ ADE có:
AC = AE (cmt)
Góc A chung
AB = AD (gt)
⇒ ΔABC = ΔADE (c.g.c)
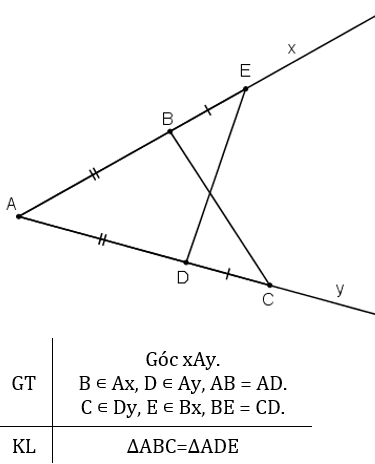
Gọi H là giao điểm của đường trung trực với đoạn AB
⇒ H là trung điểm AB và MH ⊥ AB.
Xét ΔAHM và ΔBHM có:

Nên ΔAHM = ΔBHM
Vậy MA = MB

Hướng dẫn giải.
Cách vẽ:
- Vẽ đoạn thẳng AC = 2cm
- Trên cùng một nửa mặt phẳng bờ AC vẽ các tia Ax và Cy sao cho
Hai tia cắt nhau tại B. Ta được tam giác ABC cần vẽ.
+ Hình 98: ∆ABC = ∆ABD (g.c.g) vì:
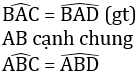
+ Hình 99:


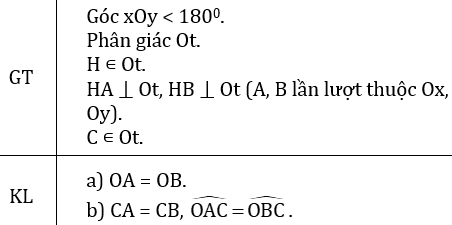
a) ΔAOH và ΔBOH có
∠ AOH = ∠ BOH (vì Ot là tia phân giác góc xOy)
OH cạnh chung
∠ OHA = ∠ OHB (= 90º)
⇒ ΔAOH = ΔBOH (g.c.g)
⇒ OA = OB (hai cạnh tương ứng).
b) ΔAOC và ΔBOC có:
OA = OB (cmt)
∠ AOC = ∠ BOC (vì Ot là tia phân giác góc xOy)
OC cạnh chung
⇒ ΔAOC = ΔBOC (c.g.c)
⇒ CA = CB (hai cạnh tương ứng)
∠ OAC = ∠ OBC ( hai góc tương ứng).
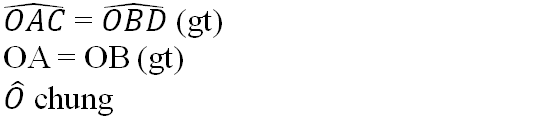
Nên ΔOAC = ΔOBD (g.c.g)
Suy ra AC = BD (hai cạnh tương ứng).
+ Hình 101: Xét ΔFDE có
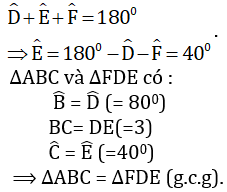
+ Hình 102 :
+ Hình 103 :

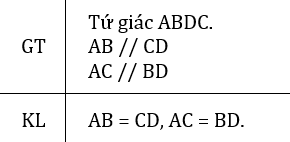
Vẽ đoạn thẳng AD
Xét ΔABD và ΔDCA có:

⇒ ΔADB = ΔDAC ( g.c.g)
⇒ AB = CD ; BD = AC (hai cạnh tương ứng).
+ Hình 105: ΔABH và ΔACH cùng vuông tại H có:
BH = CH (gt)
AH cạnh chung
⇒ ΔABH = ΔACH (hai cạnh góc vuông)
+ Hình 106: Xét ΔDKE vuông tại K và ΔDKF vuông tại K có:
DK chung
⇒ ΔDKE và ΔDKF (cạnh góc vuông – góc nhọn kề).
+ Hình 107: Xét ΔABD vuông tại B và ΔACD vuông tại C có:
AD chung
⇒ ΔABD = ΔACD (cạnh huyền – góc nhọn )
+ Hình 108:
• ΔABD = ΔACD (cạnh huyền – góc nhọn) (giống hình 107).
⇒ AB = AC và BD = CD (hai cạnh tương ứng)
• Xét ΔABH vuông tại B và ΔACE vuông tại C có
Góc A chung
AB = AC
⇒ΔABH = ΔACE (cạnh góc vuông – góc nhọn kề).
• Xét ΔDBE vuông tại B và ΔDCH vuông tại C có:
BD = DC (chứng minh trên)
⇒ ΔDBE = ΔDCH (cạnh góc vuông – góc nhọn kề)
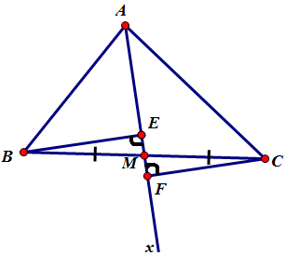
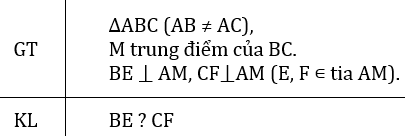
Hai tam giác vuông BME và CMF có
⇒ ΔBME = ΔCMF (cạnh huyền – góc nhọn)
⇒ BE = CF (hai cạnh tương ứng).
* Chú ý: Các em có thể suy nghĩ tại sao cần điều kiện AB ≠ AC ???
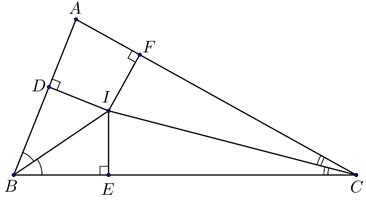
Xét ΔBID (góc D = 90º) và ΔBIE (góc E = 90º) có:
BI là cạnh chung
góc IBD = góc IBE (do BI là tia phân giác góc ABC)
⇒ ΔBID = ΔBIE (cạnh huyền - góc nhọn)
⇒ ID = IE (2 cạnh tương ứng) (1)
Tương tự, xét ΔCIE (góc E = 90º) và ΔCIF (góc F = 90º) có:
CI là cạnh chung
góc ICE = góc ICF (do CI là tia phân giác góc ACB)
⇒ ΔICE = ΔICF (cạnh huyền – góc nhọn)
⇒ IE = IF (2 cạnh tương ứng) (2)
Từ (1) và (2) suy ra: ID = IE = IF (đpcm)
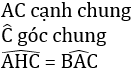
Nhưng hai tam giác này không bằng nhau vì góc AHC không phải là góc kề với cạnh AC.
Hướng dẫn giải.
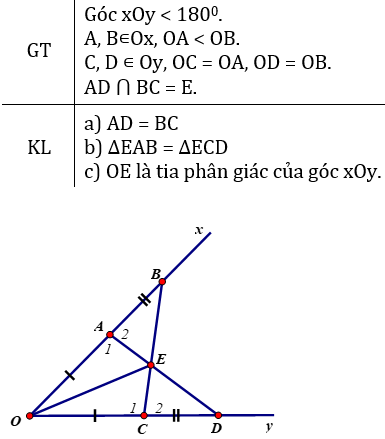
a) ΔOAD và ΔOCB có:
OA = OC (gt)
Góc O chung
OD = OB (gt)
⇒ ΔOAD = ΔOCB (c.g.c)
⇒ AD = BC (hai cạnh tương ứng).
b) Do ΔOAD = ΔOCB (chứng minh trên)
OA = OC, OB = OD ⇒ OB – OA = OD – OC hay AB = CD.
Xét ΔAEB và ΔCED có:
∠B = ∠D
AB = CD
∠A2 = ∠C2
⇒ΔAEB = ΔCED (g.c.g)
c) ΔAEB = ΔCED ⇒ EA = EC (hai cạnh tương ứng)
ΔOAE và ΔOCE có
OA = OC
EA = EC
OE cạnh chung
⇒ ΔOAE = ΔOCE (c.c.c)
⇒ 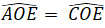
Vậy OE là tia phân giác của góc xOy.
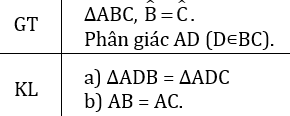
a)

Do đó ΔADB = ΔADC (g.c.g)
b) ΔADB = ΔADC ( câu a )
Suy ra AB = AC (hai cạnh tương ứng)
+ ΔAHB và ΔCKD có
HB = KD (=1)
góc AHB = góc CKD(=90º)
AH = CK (=3).
⇒ ΔAHB = ΔCKD(c.g.c)
⇒AB = CD (hai cạnh tương ứng)
+ ΔCEB và ΔAFD có
BE = DF (=2)
góc BEC = góc DFA (=90º)
CE = AF (=4).
⇒ ΔCEB = ΔAFD ( c.g.c)
⇒ BC = AD (hai cạnh tương ứng)
b) ΔABD và ΔCDB có
AB = CD
AD = BC
BD cạnh chung
⇒ ΔABD = ΔCDB (c.c.c)
⇒ góc ABD = góc CDB (hai góc tương ứng)
Vậy AB // CD ( hai gó so le trong bằng nhau )
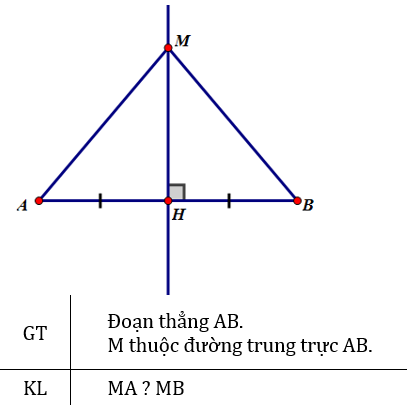
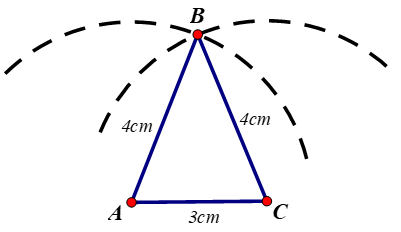
a) Vẽ đoạn thẳng AC = 3cm.
- Trên cùng một nửa mặt phẳng bờ AC vẽ cung tròn tâm A bán kính 4cm và cung tròn C bán kính 4cm.
- Hai cung tròn trên cắt nhau tại B.
- Vẽ các đoạn thẳng AB, BC ta được tam giác ABC.
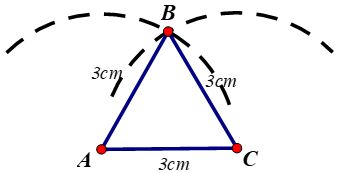
b) Vẽ đoạn thẳng AC = 3cm
- Trên cùng một nửa mặt phẳng bờ AC vẽ cung tròn tâm A bán kính 3cm và cung tròn C bán kính 3cm
- Hai cung tròn trên cắt nhau tại B
- Vẽ các đoạn thẳng AB, BC ta được tam giác ABC.
- Hình 116
Ta có ΔABD cân vì AB = AD
ΔACE cân vì AC = AE
Do AB = AD , BC = DE nên AB + BC = AD + DE hay AC = AE
⇒ ΔACE cân
- Hình 117
Ta tính được
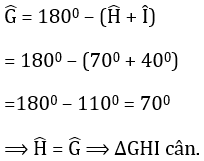
- Hình 118
* ΔOMN là tam giác đều vì ba cạnh bằng nhau OM = MN = NO
* ΔOMK cân tại M vì OM = MK
* ΔONP là tam giác cân tại N vì ON = NP

- Cắt tấm bìa hình tam giác cân.
- Gấp tấm bìa sao cho hai cạnh bên trùng nhau.
- Quan sát phần cạnh đáy sau khi gấp lại chúng trùng nhau.
Vậy hai góc ở đáy của tam giác cân bằng nhau.
a)
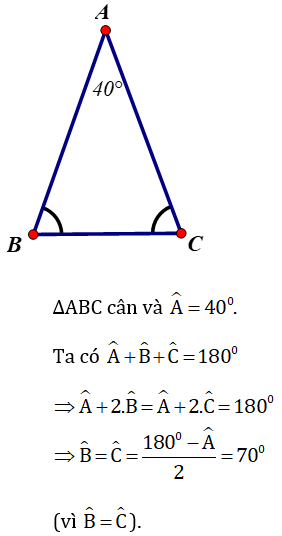
b)

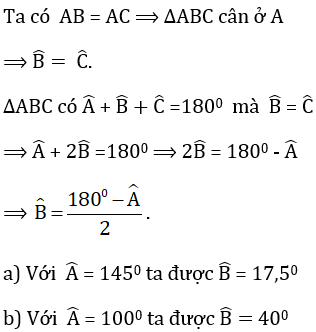
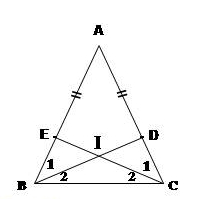

a) Xét ΔABD và ΔACE có:
AB = AC (gt)
Góc A chung
AD = AE (gt)
Nên ΔABD = ΔACE ( c.g.c)
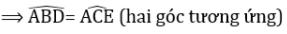
b)

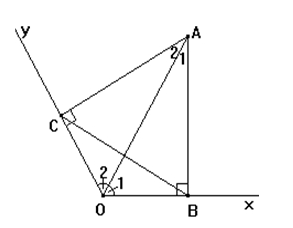

Hai tam giác vuông ABO (góc B = 90º) và ACO (góc C = 90º) có :

⇒ ΔABO = ΔACO (cạnh huyền – góc nhọn)
⇒ AB = AC (hai cạnh tương ứng) ⇒ ΔABC cân.
Tam giác cân ABC có góc A = 60º nên là tam giác đều.
- Hình a
Áp dụng định lí Pi-ta-go ta có: x2 = 122 + 52 = 144 + 25 = 169 ⇒ x = 13
- Hình b
Ta có: x2 = 12 + 22 = 1 + 4 = 5 ⇒ x = √5
- Hình c
Theo định lí Pi-ta-go 292 = 212 + x2
Nên x2 = 292 - 212 = 841 - 441 = 400 ⇒ x = 20
- Hình d
Theo định lí Pi-ta-go ta có:
x2 = (√7)2 + 32 = 7 + 9 = 16 ⇒ x = 4
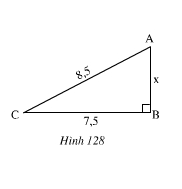
Áp dụng định lí Py–ta–go vào tam giác vuông ABC vuông tại B ta có:
AB2 + BC2 = AC2 Nên AB2 = AC2 – BC2 = 8,52 – 7,52 = 72,25 – 56,25 =16
⇒ AB = 4 (m)
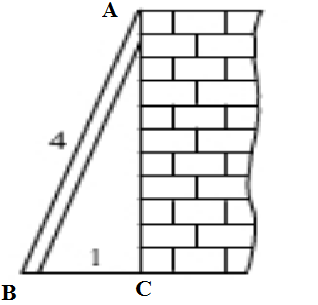
Kí hiệu như hình vẽ:
Vì mặt đất vuông góc với chân tường nên góc C = 90º.
Áp dụng định lí Pi-ta-go trong ΔABC ta có:
AC2 + BC2 = AB2 ⇒ AC2 = AB2 - BC2 = 16 - 1 = 15
⇒ AC = √15 ≈ 3,87(m) hay chiều cao của bức tường là 3,87m.
a) Ta có 92 = 81 ; 152 =225 ; 122 =144
Mà 225 = 144 + 81
Nên Theo định lí Py – ta – go đảo, tam giác có độ dài 3 cạnh 9cm ,12cm ,15cm là tam giác vuông.
b) Ta có 52 = 25 ; 132 =169 ; 122 =144
Mà 169 = 144 + 25
Nên Theo định lí Py – ta – go đảo tam giác có độ dài 3 cạnh 5dm ,13dm ,12dm là tam giác vuông.
c) Ta có 72 = 49 ; 102 =100
Mà 100 ≠ 49 + 49
Nên tam giác có độ dài 3 cạnh 7m, 7m, 10m không là tam giác vuông
AB2 + BC2 = 82 + 152 = 64+225 = 289
AC2 = 172 = 289. ⇒ AB2 + BC2 = AC2
Vậy tam giác ABC là tam giác vuông tại B (Theo định lí Py-ta-go đảo)
Ta có d2 = 202 + 42 = 400 + 16 = 416 ⇒ d = √416 ≈ 20,4 dm
Suy ra d < 21dm (là chiều cao của căn phòng)
Như vậy khi anh Nam đẩy tủ cho đứng thẳng tủ không bị vướng vào trần nhà
AC2 = AD2 + CD2 = 482 + 362 = 2304 + 1296 = 3600
⇒ AC = 60(cm)
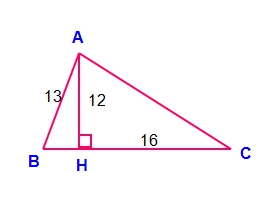
Áp dụng định lí Pi-ta-go trong ΔAHC vuông tại H ta có:
AC2 = AH2 + HC2 = 122 + 162 = 144 + 256 = 400 ⇒ AC = 20 (cm)
Áp dụng định lí Pi-ta-go trong ΔAHB vuông tại H ta có:
BH2 + AH2 = AB2 ⇒ BH2 = AB2 - AH2 = 132 - 122 = 169 -144 = 25 ⇒ BH = 5cm
Do đó BC = BH + HC = 5 + 16 = 21 (cm)
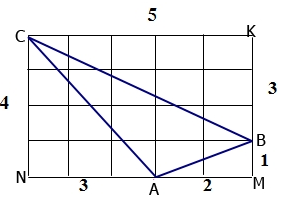
Áp dụng định lí Pi-ta-go trong ΔAMB vuông tại M ta có:
AB2 = AM2 + MB2 = 22 + 12 = 5 ⇒ AB = √5
Áp dụng định lí Pi-ta-go trong ΔANC vuông tại N ta có:
AC2 = AN2 + NC2 = 32 + 42 = 25 ⇒ AC = 5
Áp dụng định lí Pi-ta-go trong ΔBKC vuông tại K ta có:
BC2 = BK2 + KC2 = 32 + 52 = 34 ⇒ BC = √34
+) OA2 = 42 + 32 = 16 + 9 = 25 ⇒ OA = 5m < 9m
+) OC2 = 62 + 82 = 36 + 64 = 100 ⇒ OC = 10m > 9m
+) OB2 = 42 + 62 = 16 + 36 = 52 ⇒ OB = √52m ≈ 7,21 (m) < 9m
+) OD2 = 32 + 82 = 9 + 64 = 73 ⇒ OD = √73 ≈ 8,54(m) < 9m
Như vậy con Cún có thể tới các vị trí A, B, D nhưng không tới được vị trí C.
Hướng dẫn giải.
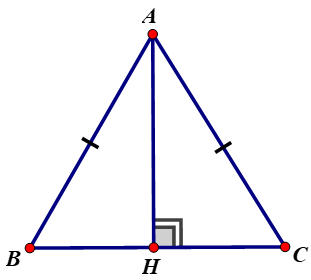
a) Xét hai tam giác vuông ΔABH và ΔACH đều vuông tại H có:
AB = AC (gt)
AH cạnh chung
Nên ΔABH = ΔACH (cạnh huyền - cạnh góc vuông)
Suy ra HB = HC
b) Ta có ΔABH = ΔACH (cmt)
Suy ra góc BAH = góc CAH (hai góc tương ứng)
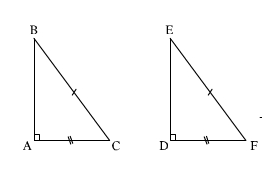
- Bổ sung AB =DE thì ΔABC = ΔDEF (c.g.c)
- Hoặc Bổ sung góc C = góc F (2 tam giác bằng nhau theo trường hợp g.c.g)
- Bổ sung BC = EF thì ΔABC = ΔDEF (cạnh huyền - cạnh góc vuông)
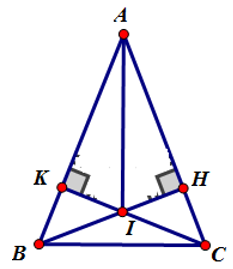

a) Xét ΔABH vuông tại H và ΔACK vuông tại K có:
AB = AC (Do ΔABC cân tại A)
góc A chung
Nên ΔABH = ΔACK (cạnh huyền – góc nhọn) ⇒ AH = AK (hai cạnh tương ứng).
b) Xét ΔAIK vuông tại K và ΔAIH vuông tại H có:
AH = AK (theo phần a)
AI chung
⇒ ΔAIK = ΔAIH (cạnh huyền – cạnh góc vuông).
⇒ góc IAK = góc IAH (hai góc tương ứng)
Vậy AI là tia phân giác của góc A.
+ Hai tam giác vuông AMD và AME 
AM chung
⇒ ΔAMD = ΔAME ( cạnh huyền - góc nhọn)
⇒ MD = ME và AD = AE ( Hai cạnh tương ứng) (1)
+ Hai tam giác vuông MDB và MEC 
MB = MC (GT)
MD = ME (chứng minh trên)
⇒ ΔMDB = ΔMEC ( cạnh huyền – cạnh góc vuông)
⇒ BD=CE ( hai cạnh tương ứng) (2)
Từ (1) và (2) ⇒ AD+BD=AE+CE ⇒ AB=AC.
+ Xét ΔAMB và ΔAMC có:
MB = MC (GT)
AB = AC (chứng minh trên)
AM chung
⇒ ΔAMB = ΔAMC (c.c.c)
Hướng dẫn giải.
1. Đúng
2. Đúng
3. Sai. Tam giác nhọn có 3 góc đều nhọn.
4. Sai. Hai góc nhọn phụ nhau.
5. Đúng.
6. Sai. Ví dụ tam giác ABC có 3 góc lần lượt là 120º, 30º, 30º là tam giác cân có góc ở đỉnh bằng 120º.
- Các tính chất ở các câu a, b được suy ra từ định lí "Tổng ba góc của một tam giác bằng 180o".
* Chứng minh:
a) ?4 bài 1 – trang 107.
b) Tam giác ABC vuông tại A
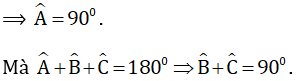
- Tính chất ở câu c được suy ra từ định lí "Trong một tam giác cân hai góc ở đáy bằng nhau".
* Chứng minh:
Giả sử có tam giác ABC đều ⇒ AB = AC =BC ⇒ ΔABC cân tại A và cân tại B
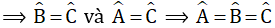
- Tính chất ở câu d được suy ra từ định lí: "Nếu một tam giác có hai góc bằng nhau thì tam giác đo là tam giác cân".
* Chứng minh:
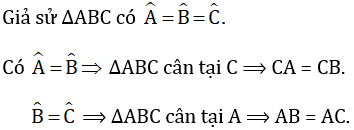
⇒ AB = AC = BC ⇒ ΔABC là tam giác đều.
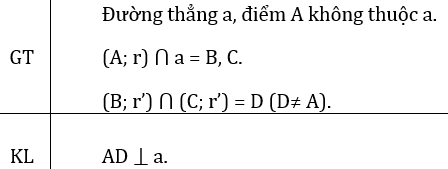
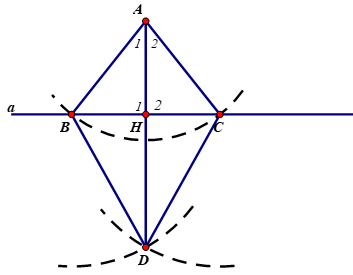
Gọi bán kính cung tròn tâm A là r, bán kính cung tròn tâm B và C là r’.
Xét ΔABD và ΔACD có:
AB = AC (=r)
DB = DC (=r')
AD cạnh chung
Nên ΔABD = ΔACD (c.c.c)
- Gọi H là giao điểm của AD và a
ΔAHB và ΔAHC có
AB = AC (= r)
AH cạnh chung
⇒ ΔAHB = ΔAHC (c.g.c)
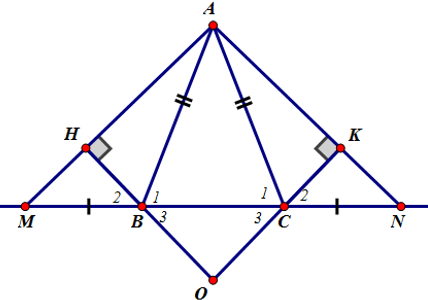

a) ΔABC cân tại A suy ra
Ta lại có :
- ΔABM và ΔACN có
AB = AC (Do ΔABC cân tại A).
BM = CN(gt)
⇒ ΔABM = ΔACN (c.g.c)
⇒ AM = AN (hai cạnh tương ứng) ⇒ ΔAMN cân tại A.
b) Xét ΔBHM vuông tại H và ΔCKN vuông tại K có:
BM = CN (gt)
⇒ ΔBHM = ΔCKN (cạnh huyền – góc nhọn)
⇒ BH = CK (hai cạnh tương ứng)
c) Theo câu b ta có ΔBHM = ΔCKN ⇒ HM = KN (hai cạnh tương ứng)
Mà AM = AN ⇒ AM –MH = AK – KN hay AH = AK.
d) ΔBHM = ΔCKN
Vậy tam giác OBC là tam giác cân tại O.
e) Khi góc BAC = 60º và BM = CN = BC
Tam giác cân ABC có góc BAC = 60º nên là tam giác đều
⇒ AB = BC và góc B1 = 60º
Ta có: AB = CB, BC = BM (gt) ⇒ AB = BM ⇒ ΔABM cân ở B ⇒
Mà theo tính chất góc ngoài trong ΔBAM thì
Tương tự ta có
* Ta chứng minh tam giác OBC là tam giác đều.
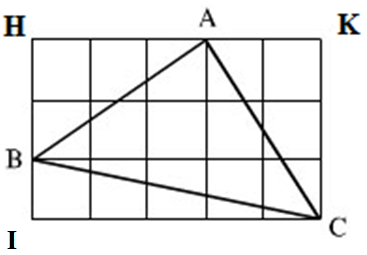
Gọi độ dài mỗi ô vuông là 1:
- Áp dụng định lý Pytago vào tam giác AHB vuông tại H ta có : AB2 = AH2 + HB2 = 32 + 22 = 13.
- Áp dụng định lý Pytago vào tam giác AKC vuông tại K ta có : AC2 = AK2 + KC2 =22 + 32 = 13.
- Áp dụng định lý Pytago vào tam giác BIC vuông tại I có: BC2 = BI2 + IC2 = 12 + 52 = 26.
Nhận thấy AB2 = AC2 ⟹ AB = AC nên ∆ABC cân tại A (1)
Áp dụng định lý Pytago đảo ta thấy AB2 + AC2 = 13 + 13 = 26 = BC2 nên ∆ABC vuông tại A (2)
Từ (1) và (2) suy ra ∆ABC vuông cân tại A.
a) Xếp tam giác đều: Xếp tam giác với mỗi cạnh là bốn que diêm.
b) Một tam giác cân mà không đều: 2 cạnh bên 5 que diêm, cạnh đáy 2 que.
c) Xếp tam giác vuông: Xếp tam giác có các cạnh lần lượt là ba, bốn và năm que diêm. (Cạnh huyền 5 que diêm, 2 cạnh bên lần lượt là 3, 4 que diêm vì 52 = 32 + 42).
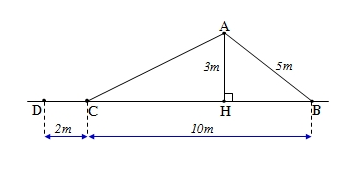
+ ΔAHB vuông tại H
Theo định lí Py–ta- go ta có
HB2 = AB2 – AH2 = 52 – 32 =25 - 9 =16
Suy ra HB = 4 (m)
Suy ra HC = BC – HB = 10 - 4 = 6(m)
+ ΔAHC vuông tại H
Theo định lí Py-ta-go ta có
AC2 = AH2 + HC2 = 32 + 62 = 9 + 36 = 45.
Suy ra AC = √45 ≈ 6,7(m)
Độ dài đường trượt ACD bằng: 6,7 + 2= 8,7 (m)
Và hai lần đường lên BA bằng 5.2 =10 (m)
Đo độ dài đường trượt ACD chưa bằng hai lần đườg lên BA
Vậy bạn Mai nói sai, bạn Vân nói đúng.





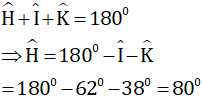
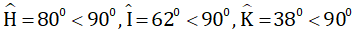







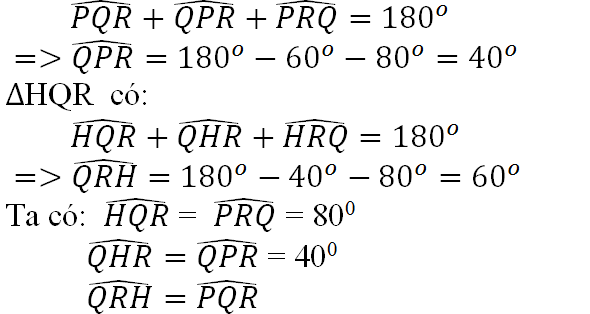




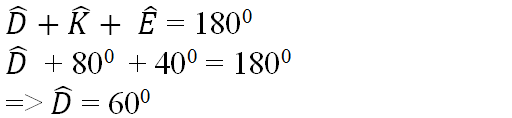





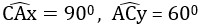
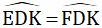
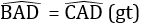
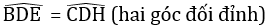









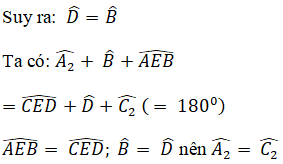





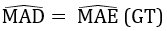



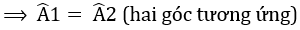
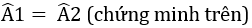

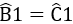
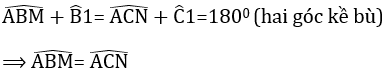
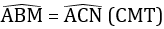
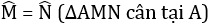

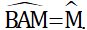
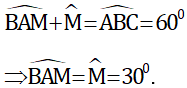
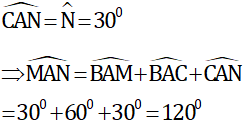



Nhận xét
Đăng nhận xét