[HH12] KHỐI ĐA DIỆN - &02. Thể tích khối đa diện.
Hướng dẫn giải.
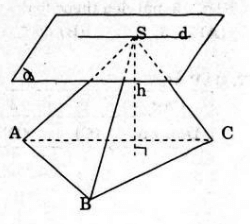
Thể tích hình chóp S.ABC là :
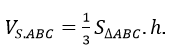
Trong đó SΔABC không đổi, h = d(S; (ABC))
a) Khi S di chuyển trên mp (α)// (ABC) thì d(S, (ABC)) = d((α);(ABC)) không đổi nên VVS.ABC không đổi.
b) Khi S di chuyển trên một mặt phẳng song song với một cạnh đáy. Mặt phẳng này có thể không song song với mp (ABC).
Khi đó h = d(S: (ABC)) có thể thay đổi nên VS.ABC có thể thay đổi.
c) Giả sử S di chuyển trên ∆ và ∆ // AC
Do ∆ // AC ⇒ ∆ //(ABC) ⇒ d(S, (ABC)) = d(∆; (ABC)) không đổi nên VS.ABC không đổi.
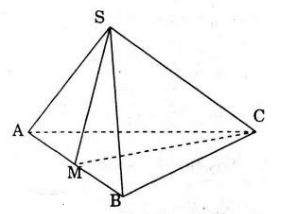
Gọi M là một điểm trên đoạn thẳng AB. Khi đó (SMC) chia tứ diện S.ABC thành hai tứ diện S.AMC và S. BMC lần lượt với thể tích V1,2
Vì d(S, (AMC) = d(S,(BMC)) nên
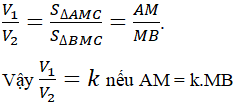
Kết luận: Lấy điểm M trên AB sao cho AM = k.MB. Khi đó, khối tứ diện SABC được chia thành hai khối tứ diện SAMC và SBMC thỏa yêu cầu bài toán.
* Ta tính thể tích khối tứ diện đều AA’B’D’.
Gọi H là tâm của tam giác đều A’B’D’ cạnh a và O là giao điểm của A’C’ và B’D’
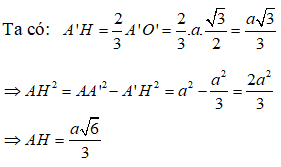
Vì (ABCD)// mp (A’B’C’D’ nên:
d( H, ( A’B’C’D’))= d( (ABCD), (A’B’C’D’)) = AH =
Diện tích tam giác đều A’B’D’ cạnh a là:
Diện tích tứ giác A’B’C’D’ là:
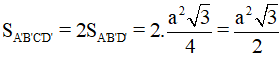
Thể tích hình hộp đã cho là:
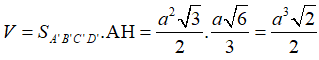
- Xét lăng trụ n – giác đều A1 A2…An A1' A2'…An' có tất cả các cạnh bằng a.
Ta có: V = S.h, trong đó
S là diện tích n – giác đều A1 A2…An cạnh a.
h là chiều cao.
V là thể tích của lăng trụ.
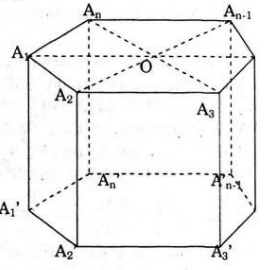
Theo đề ra: h = a.
* Gọi O là tâm của đáy A1 A2…An.
Xét tam giác OA1 A2. Gọi H là trung điểm của A1 A2.
⇒ H là trung điểm của A1 A2:
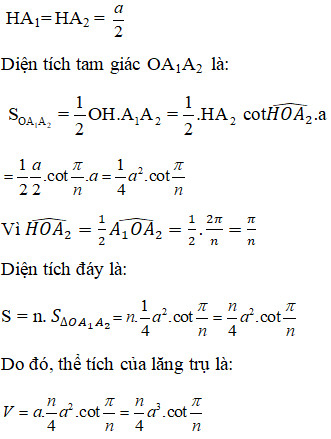
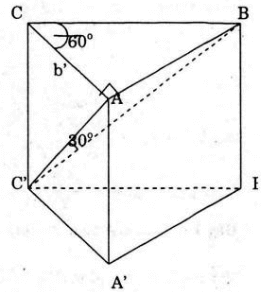
a) Do ABC.A’B’C’ là lăng trụ đứng nên AA’ ⊥ AB mà AC ⊥ AB.
⇒ AB ⊥ (ACC’A’) ⇒ góc BC'A=30o và ΔABC' vuông tại A. ⇒ AC’ = AB.cot 30o
Xét ΔABC:
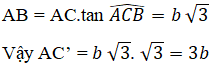
b) VABC.A'B'C'=SΔABC.h. Trong đó
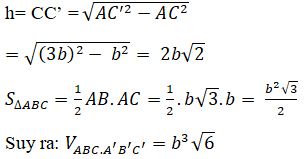
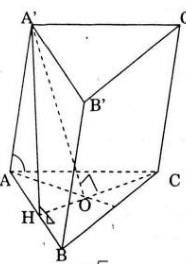
a) Gọi O là tâm của tam giác ABC, vì OA = OB = OC nên A' O ⊥ (ABC)
Suy ra, OA = OB = OC
Lại có: A’A = A’B = A’C
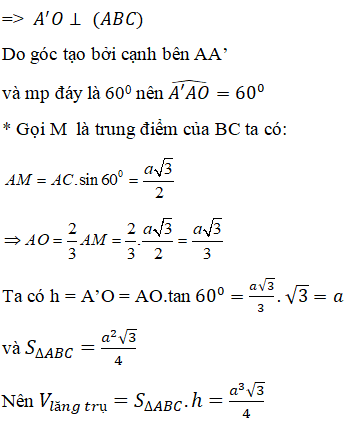
b) Ta có: BC ⊥ AO nên BC ⊥ AA' (định lí 3 đường vuông góc)
Lại có AA’ //CC’ => BC ⊥ CC’
Tứ giác BB’C’C là hình bình hành có một góc vuông nên là hình chữ nhật.
c) Gọi H là trung điểm của AB .
Ta có: AB⊥(A^' HO)nên A^' H⊥AB
Trong tam giác vuông A’OH có:
Diện tích hình bình hành ABB’A’ là :
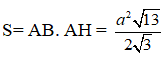
Tương tự, diện tích hình bình hành ACC’A’ là:
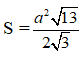
Diện tích hình chữ nhật BCC’B’ là
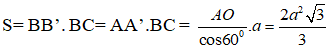
Vậy diện tích xung quanh của hình lăng trụ là:
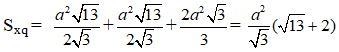
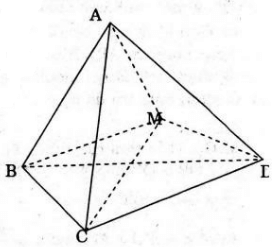
Gọi h1,h2,h3,h4 lần lượt là khoảng các từ M đến (ABC), (ACD), (ABD), (BCD). Khối tứ diện ABCD được chia thành 4 khối tứ diện MABC, MACD, MABD, MBCD.
Ta có:
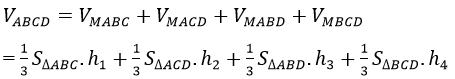
Lại vì SΔABC=SΔACD=SΔABD=SΔBCD
Nên VABCD=(1/3).S_ΔABC (h1+h2+h3+h4) (1)
Gọi h là chiều cao của tứ diện đều, ta có:
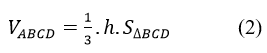
Từ (1) và (2) có: h1+h2+h3+h4=h
Vậy khoảng cách từ M đến 4 mặt của hình tứ diện là một số không phụ thuộc vào vị trí của M.
* Xét tứ diện đều ABCD có cạnh là a. Ta tính h.
Gọi là trực tâm của tam giác đều BCD và M là trung điểm của CD
Ta có:

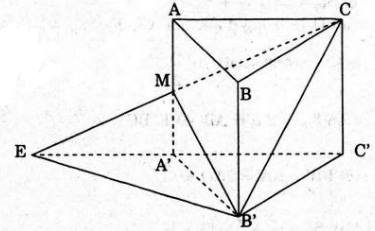
Gọi V, S, h lần lượt là thể tích và diện tích đáy, chiều cao của lăng trụ: V= S.h. V1,V2 lần lượt là thể tích phần lăng trụ bên trên, bên dưới thiết diện MB’C
E = CM ∩ C'A', do M là trung điểm của AA’ nên A’E = A’C’
SΔEA'B'=SΔA'B'C' =S
Ta có:
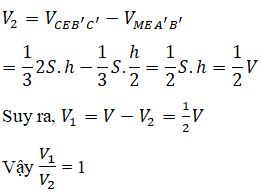
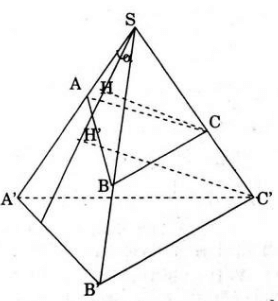
Ta có:
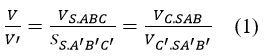
Kẻ CH, C’H’ vuông góc với (SAB) (H, H’ ∈ (SAB)) => CH // C’H’ và S, H, H’ thẳng hàng. Theo định lí Ta- let ta có:
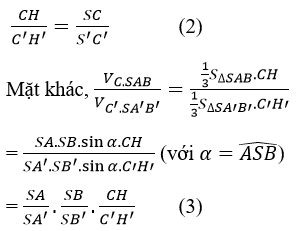
Từ (1), (2) và (3) suy ra:
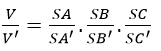
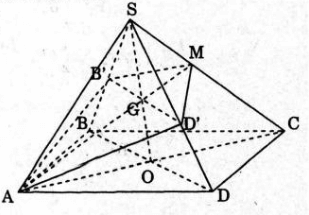
Gọi B’= (P) ∩SB; D’ = (P) ∩SD;O=AC ∩BD
Khi đó: B’D’, AM, SO đồng quy tại trọng tâm G của ΔSAC và B’D’ // BD (do (P) // BD)
Cách 1.
Ta có:
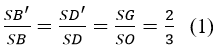
Lại có: GB’ = GD’
=> SΔAB'M=SΔAD'M (2)
Từ (1) và (2) suy ra:
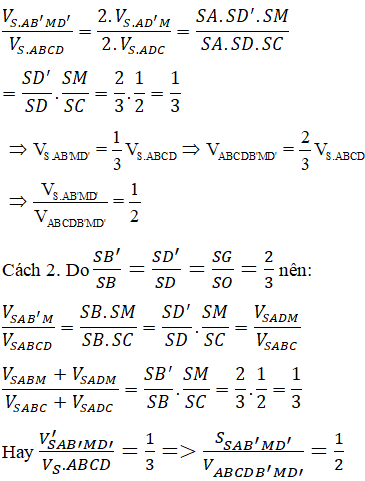
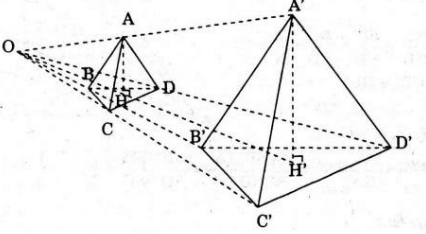
Gọi H là hình chiếu của A trên (BCD). Giả sử phép vị tự tỉ số k biến A, B, C, D, H lần lượt thành A’, B’, C’, D’, H’.
Hơn nữa, theo tính chất của phép vị tự thì:
A’H’ song song hoặc trùng hợp với AH;
Và (B’C’D’) song song hoặc trùng hợp với (BCD)
Mà AH ⊥ (BCD) nên A'H'⊥(B'C'D').
Vậy A’H’ là đường cao của tứ diện (A’B’C’D’) (1)
Mặt khác, dễ thấy:
Hơn nữa, cũng từ tính chất của phép vị từ ta có:
Từ (1), (2), (3) ta có:
Hướng dẫn giải Ôn tập chương 1.
- Khối lăng trụ n – giác có 2n đỉnh, 3n cạnh và n + 2 mặt.
- Khối chóp n – giác có n + 1 đỉnh, 2n cạnh và n + 1 mặt.
- Khối đa diện đều loại {3; 3} là tứ diện đều, mỗi đỉnh là đỉnh chung của 3 cạnh.
- Khối đa diện đều loại {3, 4} là khối 8 mặt đều, mỗi đỉnh là đỉnh chung của 4 cạnh.
- Khối đa diện đều loại {3, 5} là khối 20 mặt đều, mỗi đỉnh là đỉnh chung của 5 cạnh.
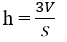
- Hình tứ diện đều có 6 mặt phẳng đối xứng. đó là các mặt phẳng đi qua một cạnh và trung điểm của cạnh đối diện.
- Hình lập phương có 9 mặt phẳng đối xứng, gồm 3 mặt phẳng trung trực của 3 cạnh cùng xuất phát tại một đỉnh; các mặt phẳng xác định bởi một cặp cạnh đối diện của hình lập phương.
- Hình bát diện đều ABC.DEF có 9 mặt phẳng đối xứng gồm: (ABCD), (BEDF), (AECF), mặt phẳng phẳng trung trực của các cạnh AB, AD, AF, BE, BF.
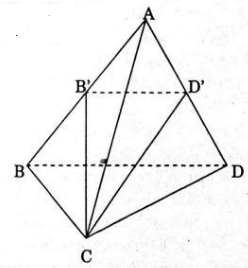
Mặt phẳng (CB’D’) chia khối tứ diện ABC thành hai khối chóp là AB’CD’ và C.BB’D’D ta có:
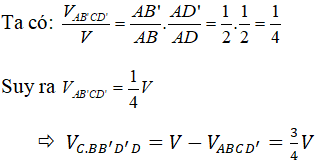
Gọi O là giao điểm của các đường chéo của hình hộp. Ta có O là trung điểm của AC’, tứ giác AMC’Q là hình bình hành nên O là trung điểm của MQ.
Vậy O, M, Q thẳng hàng. Hơn nữa MN, SP, RQ đôi một song song và lần lượt đi qua O, M, Q nên M, N, P, Q, R, S cùng nằm trên mp(α) đi qua O (và mp(α) // (ACD’)).
Ta thấy O là trung điểm của AC’, BD’, A’C, B’D, MQ, NR, SP nên (α) chia khối hộp thành hai phần là ảnh của nhau qua V(O,-1) (hay phép đối xứng tâm O). Do đó chúng có thể tích bằng nhau.
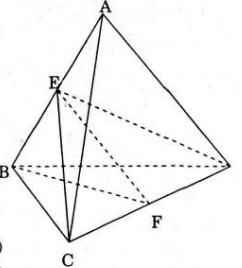
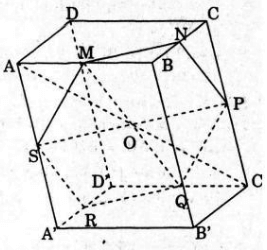
a) Hai mp( ABF) và (CDE) chia khối tứ diện ABCD thành 4 khối tứ diện là:
BCEF, ACEF, BDEF, ADEF.
b) Do E là trung điểm của AB nên S∆BEF=S∆AEF ⇒ VCBEF = VCAEF và VDBEF = VDAEF (1)
Tương tự S∆CEF = S∆DEF và VACEF = VADEF (2)
Từ (1) và (2), suy ra: VBCEF=VADEF=VBDEF=VADEF
c) Nếu ABCD là khối tứ diện đều thì (CED), (ABF) là các mặt phẳng đối xứng của tứ diện.
Cách 1.
Ta có: phép đối xứng qua (ABF) biến tứ diện BCEF thành tứ diện ADEF; biến tứ diện ACEF thành ADEF (1)
Phép đối xứng qua (CED) biến tứ diện DBEF thành tứ diện CAEF ; biến tứ diện BDEF thành ACEF. (2)
Từ (1) và (2) suy ra các tứ diện BCEF, ACEF, ADEF, BDEF bằng nhau.
Cách 2. Thực hiện phép đối xứng qua mặt phẳng (ABF).
Ta có: tứ diện BCEF biến BDEF, AECF biến thành AEDF (1)
Do EF là trục đối xứng qua đường thẳng EF biến tứ diện BCEF thành ADEF (2)
Từ (1) và (2) đpcm.
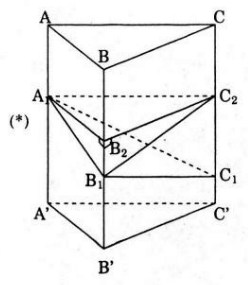
a) Không làm mất tính tổng quát, giả sử a≤b≤c.
Trên cạnh BB’ lấy B2 sao cho BB2=a ; B1B2=b-a
Trên cạnh CC’ lấy C2 sao cho CC2=a ; C1C2=c-a
Ta có: VABC.A1 B1 C1 =VABC.A1 B2 C2+VA1 B2 C2 B1+VA1 B1 C2 C1
Trong đó:
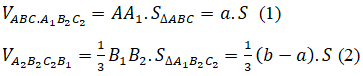
(vì B1 B2⊥(A1 B2 C2 ); ∆A1 B2 C2=∆ABC)
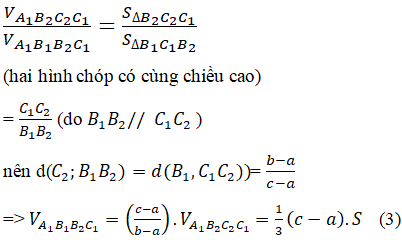
Thay (1), (2) và (3) và (*) ta được:
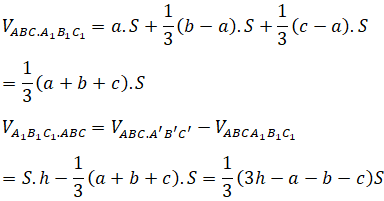
b) Để thể tích hai phần đó bằng nhau, ta có:
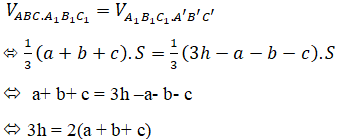
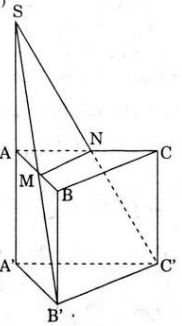
Gọi V1 là thể tích của phần chứa cạnh AA’, V2 là thể tích phần còn lại
S là diện tích đáy A’B’C’, h là chiều cao của lăng trụ và V là thể tích của lăng trụ. Do BC//B’C’ nên (ABC) cắt (MB’C’) theo giao tuyến là đường thẳng d qua M và d // BC.
Gọi N = d ∩ AC. Ba mp(AA’B’); mp(ACC’A’) và (B’C’M) cắt nhau theo ba giao tuyến là AA’; MB’ và NC’. Suy ra, ba giao tuyến này đồng quy với nhau tại S.
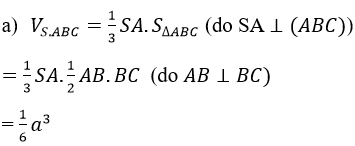
b) Cách 1. Ta có: BC⊥AB (gt) ; BC⊥SA (do SA⊥(ABC))
=>BC⊥(SAB)=>SB là hình chiếu của SC trên (SAB)
Mặt khác: SA = AB (do đều bằng a) và B’ là trung điểm của SB nên AB'⊥SB . vậy AB'⊥SC (1) (định lí 3 đường vuông góc)
Lại có, C’ là hình chiếu của A trên SC nên AC’⊥ SC (2)
Từ (1), (2) suy ra SC⊥(AB'C')
Cách 2.
Ta có: BC ⊥(SAB) vì (BC ⊥AB,BC⊥SA do SA ⊥(SAB) => BC ⊥AB'
Lại có SB ⊥AB'(trung tuyến trong tam giác cân)
Vậy AB’ ⊥(SBC)=> AB'⊥SC (1)
Mặt khác C’ là hình chiếu của A trên SC nên AC’ ⊥ SC (2)
Từ (1), (2) suy ra SC ⊥(AB'C' )
c) Tính VS.AB'C'?
Cách 1. Vì SC'⊥AB'C' nên:
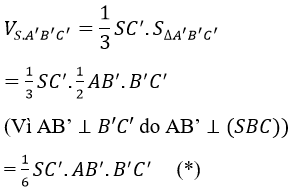

(trung tuyến trong tam giác vuông)
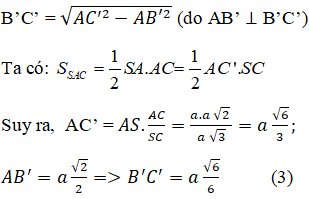
Thay (1), (2), (3) vào (*) ta được:
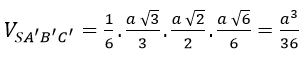
Nhận xét:
Ta có: AB'⊥(SBC) nên có thể lấy V = (1/3)AB'.SΔSB'C'=(1/6). AB'.B' C'.SC' rồi giải như cách 1.
Cách 2: ta có:
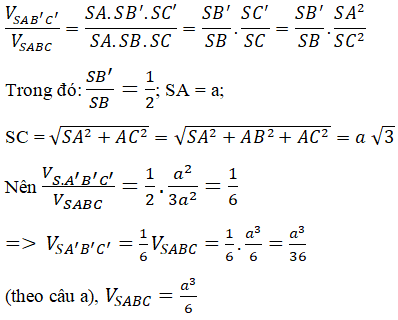
Chọn C
Chọn B
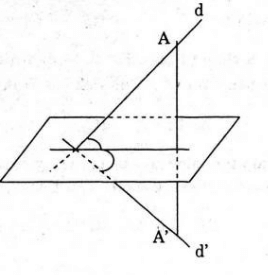
Vì d, d’ phân biệt và đồng phẳng nên d // d’ hoặc d cắt d’.
- Nếu d // d’ thì có 1 phép đối xứng qua mặt phẳng biến d thành d’, (đó là mặt phẳng song song với mặt phẳng (d, d’) và cách đều hai đường thẳng d và d’.
- Nếu d cắt d’, có 2 phép đối xứng qua mặt phẳng biến d thành a’ (xem câu 4).
Chọn D
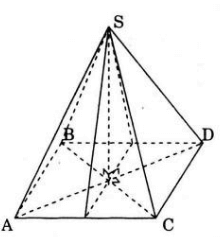
Hình chóp tứ giác đều S.ABCD có 4 mặt phẳng đối xứng là: (SAC), (SBD), mặt phẳng trung trực của các cạnh AB, AD,
Chọn D
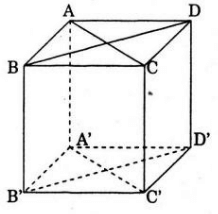
Hình thoi có hai đường chéo vuông góc và cắt nhau tại trung điể, của mỗi đường, ABCD.A’B’C’D’ là hình hộp đứng có đáy là hình thoi (không phải hình vuông) có các mặt phẳng đối xứng là: (ACC’A’), (BDD’B’), mặt phẳng trung trực của cạnh AA’
Chọn C
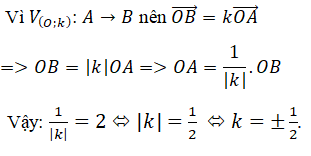
Chọn C
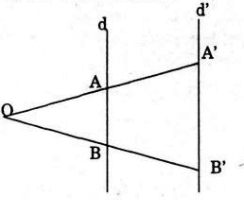
- Nếu O ∈ mp(d,d’) thì có 1 phép vị tự nào biến d thành d’.
- Nếu O ∉ mp(d, d’). Không có phép vị tự tâm O nào biến d thành d.
Chọn D
Chọn D
Chọn B
Chọn C
Diện tích 1 mặt là S = a2.
Tổng diện tích các mặt là St = 6a2 = 96 ⇒ a = 4.
Do đó, thể tích của hình lập phương là: V = 43 = 64
Chọn A
Vậy 3 kích thước là: 6, 12, 24 => Chọn D
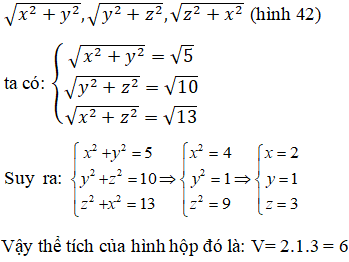
Chọn C
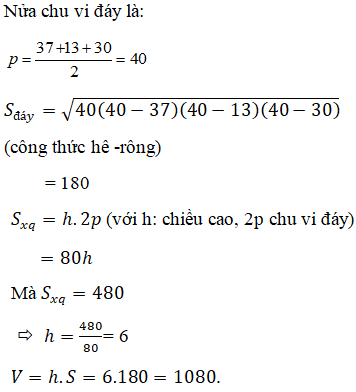
Chọn C

Chọn B
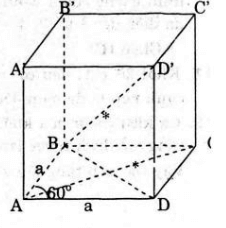
Gọi O là giao điểm của AC và BD.
* Tam giác ABD là tam giác cân có 1 góc bằng 60º nên tam giác này đều
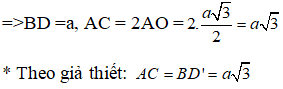
Xét tam giác BDD’ có:
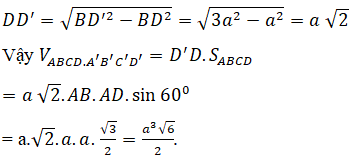
Chọn D
Ta có: VH'=(a+2)2,VH=a3
Theo gt: VH' - VH=98 <=> (a+2)3-a3=98 ⇔ a3 + 6a2 + 12a + 8 – a3 = 98 ⇔ 6a2 + 12a -90 = 0
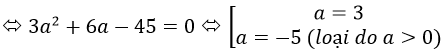
Chọn D
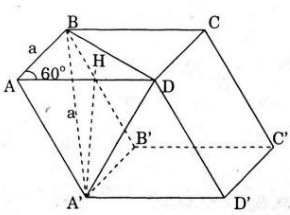
Xét hình hộp ABCD.A’B’C’D’ có các mặt đều là hình thoi cạnh a góc nhọn là 60o.
Trong ΔABD, có góc BAD=60o (gt)
Và AB = AD (cùng bằng a) nên ΔABC đều cạnh a.
=> BD = a, tương tự các hình đường chéo nhỏ của các mặt hình hộp đều bằng a.
=> A’D = A’B = BD = A’A = AB = AD = a
Hay A'.ABD là tứ diện đều cạnh a nên đường cao A'H=a √6/3
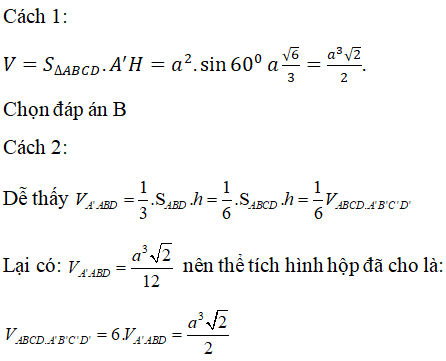
Chọn B
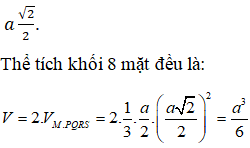
Chọn D
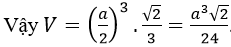
( dùng công thức tính nhanh)
Chọn A
Gọi V1,V2,V3,…V12 thể tích của 12 hình chóp tam giác đều trên, h1,h2,…h12 là chiều cao của chúng (khoảng cách từ M đến các mặt).
Ta có:
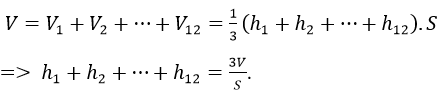
Chọn C
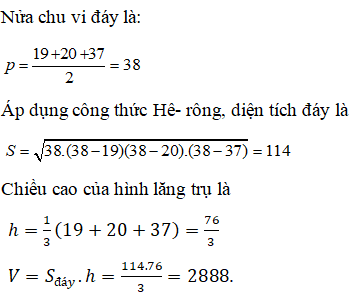
Chọn A
Chọn B
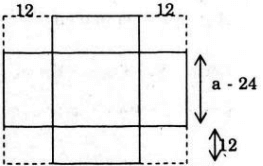
Gọi a là độ dài cạnh hình vuông ban đầu. (cm) (a > 24)
Hình hộp chữ nhật có các kích thước là: a - 24, a - 24 và 12 (cm)
Thể tích khối hộp đó là: V = 12. (a-24)2 <=> 4800 = 12.(a-24)2 <=> a = 44.
Chọn C
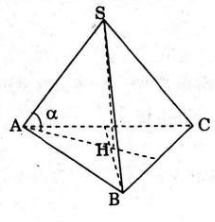
Xét chóp tam giác đều S.ABC. Gọi H là hình chiếu của S trên (ABC)
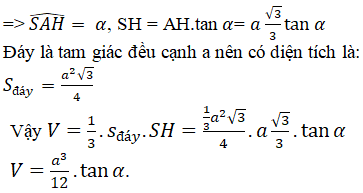
Gọi H là tâm của tam giác đều.
Lại có, SA = SB = SC = b nên SH vuông góc với (ABC) và góc SAH = α
Gọi I là trung điểm của BC. Ta có:

Chọn B.
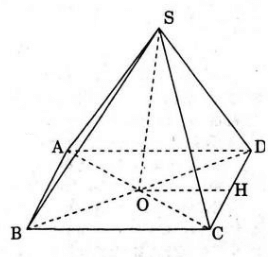
Gọi độ dài cạnh đáy của hình chóp là a.
Do đáy là hình vuông và có diện tích là 4 nên ta có: a2 = 4 ⇒ a = 2.
Gọi O là hình chiếu của S trên (ABCD)
Suy ra, O là tâm của đáy và SO vuông góc với mp (ABCD)
Thể tích của hình chóp đã cho là:
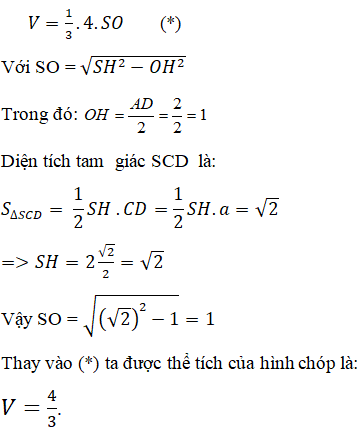
Chọn đáp án C
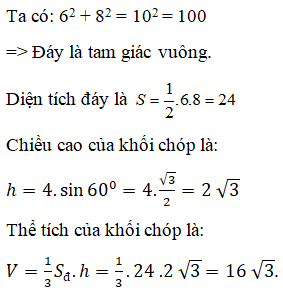
Chọn A
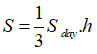
Khi mỗi cạnh tăng lên n lần thì Sđáy tăng lên n2 lần và h tăng n lần.
Vậy V tăng n3 lần. Chọn C
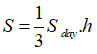
Khi mỗi cạnh giảm n lần thì Sđáy giảm n2 lần mà h tăng lên n lần. Vậy V giảm đi n lần.
Chọn D.














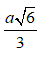
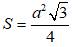
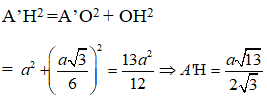
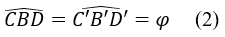
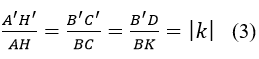
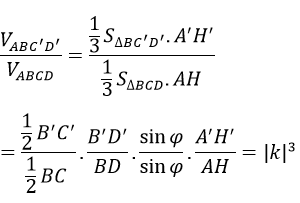
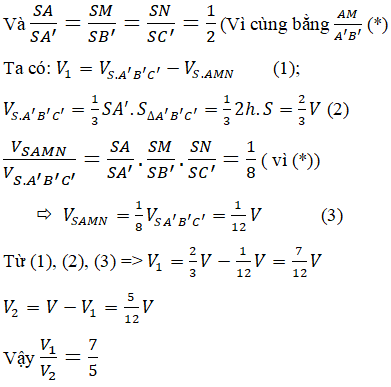
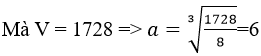


NTH_AT_17 đã đọc và hiểu
Trả lờiXóaNTH_AT_12 đã học và hiểu
Trả lờiXóaNTH-AT-05 đã đọc và hiểu
Trả lờiXóaNTH-AT-02 đã đọc và hiểu
Trả lờiXóaNTH-AT-23 đã đọc và hiểu
Trả lờiXóaNTH-AT-18 đã đọc và hiểu
Trả lờiXóaNTH-AT-07 đã đọc và hiểu
Trả lờiXóaNTH_AT_11 đã đọc và hiểu
Trả lờiXóaNTH-A4-36 đã đọc và hiểu
Trả lờiXóaNTH - A5 - 37 đã đọc và hiểu ạ.
Trả lờiXóaNTH-A2-33 đã đọc và hiểu
Trả lờiXóa