[HH12] KHỐI ĐA DIỆN - &01. Khối đa diện đều và phép biến hình trong không gian
Hướng dẫn giải.
- Giải sử khối đa diện đã cho có M mặt và C cạnh.
Vì mỗi mặt có 3 cạnh nên M mặt có 3M cạnh, nhưng mỗi cạnh lại là cạnh chung cho 2 mặt nên có 2C = 3M, suy ra M chẵn. vậy nếu khối đa diện có các mặt làm tam giác thì số mặt phải là số chẵn.
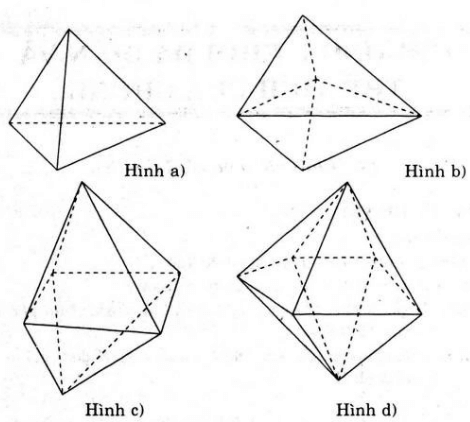
- Khối a) khối tứ diện có 4 mặt là tam giác.
- Hình b) khối 6 mặt là tam giác.
- Hình c) khối 8 mặt là tam giác.
- Hình d) khối 10 mặt là tam giác
Vì mỗi đỉnh là đỉnh chung của ba cạnh nên Đ đỉnh có 3 Đ cạnh, nhưng mỗi cạnh là cạnh chung của 2 đỉnh.
Vậy 2C = 3Đ. Từ đó suy ra Đ là số chẵn.

Gọi A là một đỉnh của khối đa diện. A là đỉnh chung của 3 cạnh AB, AC, AD. Mặt chứa cạnh AB, AC, AD phải là ΔABC, tương tự ΔACD, ΔADB cũng là các mặt của đa diện. vậy xuất phát từ đỉnh D của đa diện có các cạnh DC, DB, nên mặt chứa cạnh DB và Dc phải là ΔBCD dây là mặt thứ 4 của đa diện. Từ đó suy ra kết quả bài toán.
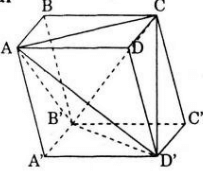
Khối hộp ABCDA’B’C’D’ được chia thành 5 khối tứ diện CB’C’D’; BCB’A; AA’B’D’; DACD’; B’ACD’; bởi các mặt phẳng (CB’D’), (ACB’), (ABD’), (ACD’).

Gọi M, N là hai điểm trên cạnh AB, CD (khác hai đầu nút). Khi đó hai mặt phẳng (ABN) và (CMD) chia khối tứ diện ABCD thành bốn khối tứ diện: CBMN, DBMN, CAMN, DAMN.
Hướng dẫn giải.
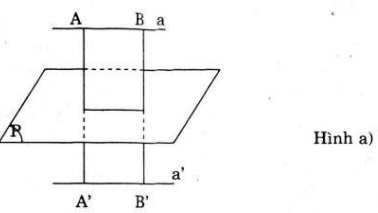
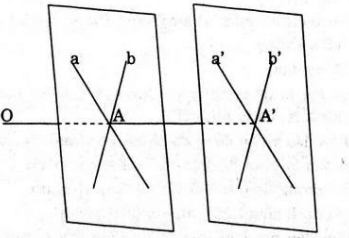
a)+ Nếu a ⊂ (P), khi đó, lấy điểm A bất kì trên a thì A∈ (P) nên Đ biến A thành A'≡ A. vậy Đ biến a thành a’ ≡a
+ Nếu a ⊥ (P). lấy A bất kì trên a. nếu Đ biến A thành A’ thì AA’ ⊥ (P) mà a ⊥ (P), (A) ∈ a ⇒ A' ∈ a ⇒ a' ≡ a
Vậy nếu đường thẳng a nằm trong mp(P) hoặc đường thẳng a vuông góc với mp(P) thì qua Đ biến đường thẳng a thành a’ ≡ a.
b)+ Nếu a // (P). lấy 2 điểm A, B phân biệt trên a giả sử Đ biến A thành A’, B thành B’. Ta thấy tứ giác ABB’A’ là hình chữ nhật nếu A’B’ // AB hay a’ // a
Vậy để a // a’ thì a// (P).
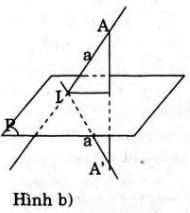
c)+ a cắt (P) tại I nhưng không vuông góc với (P). Khi đó, Đ biến I thành chính nó (vì I ∈(P) và biến A ∈a (với A không trùng I) thành A’ sao cho (P) là mặt phẳng trung trực của AA’. Vậy Đ biến AI thành A’I.
Do a không vuông góc với (P) nên dễ thấy A, I, A’ không thẳng hàng hay AI, A’I cắt nhau tại I tức a, a’ cắt nhau.
Vậy a cắt a’ nếu a cắt (P) nhưng a không vuông góc với (P).
d) a, a’ chéo nhau không xảy ra.
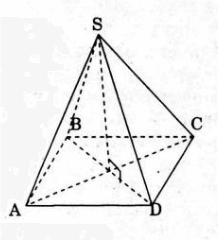
a) xét hình chóp tứ giác đều S.ABCD
- Dễ thấy (SAC) là mặt phẳng trung trực của BD nên phép đối xứng qua (SAC) biến các đỉnh S, A, B, C D lần lượt thành các đỉnh S, A, D, C, B hay biến hình chóp S.ABCD thành chính nó. Vậy (SAC) là một mặt phẳng đối xứng của hình chóp S.ABCD.
Tương tự (SBD) cũng là một mp đối xứng của hình chóp S.ABCD .
- Lại có, mặt phẳng trung trực của cạnh AB đồng thời là mặt phẳng trung trực của cạnh CD và chứa S nên đó là một mặt đối xứng của hình chóp S.ABCD. tương tự mặt phẳng trung trực của AD cũng là một mặt phẳng đối xứng của hình chóp S.ABCD.
- Kết luận: Hình chóp tứ giác đều S.ABCD có 4 mặt phẳng đối xứng là (SAC), (SBD) , mặt phẳng trung trực của cạnh AD và AD.
b) Xét hình chóp cụt tam giác đều ABC.A’B’C’
Gọi S là điểm đồng quy của AA’, BB’, CC’, M, N, P lần lượt là trung điểm của BC, CA, AB.
Ta có (SAM) là mặt phẳng trung trực của BC, cũng là mặt phẳng trung trực của B’C’.
Mặt khác, A’ ∈ SA => A’ ∈ mp (SAM). Vậy phép đôi xứng qua mp(SAM) biến các đỉnh A, B, C, A’, B’, C’ lần lượt thành A, C; B, A’, C’, B’ do đó biến hình chóp cụt tam giác đều ABC.A’B’C’ thành chính nó hay (SAM) là một mp đối xứng là (SAM), (SBN), (SCP).
Tương tự các mặt phẳng là (SBN), (SCP) cũng là mặt phẳng đối xứng.
c) Xét hình hộp chữ nhật ABCD.A’B’C’D’ mà không có mặt nào là hình vuông.
- Gọi (P) là mặt phẳng trung trực của cạnh AB thì (P) cũng là mặt phẳng trung trực của các cạnh CD, D’C’, A’B’ nếu cho phép đối xứng qua (P) biến A, B, C, D, A’, B’, C’, D’ lần lượt thành B, A, D, C, B’, A’, D’, C’ hay phép đối xứng qua (P) biến hình hộp của hình chữ nhật ABCD.A’B’C’D’ thành chính nó. Vậy (P) là một mặt phẳng đối xứng của hình hộp chữ nhật.
Tương tự, mặt phẳng trung trực của các cạnh AA’, AD cũng là các mặt phẳng đối xứng của hình hộp chữ nhật ABCD.A’B’C’D’.
Kết luận: hình hộp chữ nhật mà không có mặt phẳng nào vuông góc có 3 mặt phẳng đối xứng là 3 mặt phẳng trung trực của 3 cạnh cùng xuất phát tại một đỉnh.
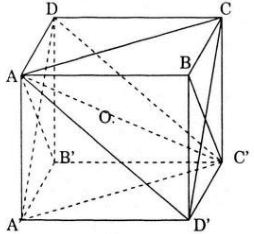
a) Cách 1: Do ABCD.A’B’C’D’ là hình lập phương nên phép đối xứng qua mặt phẳng trung trực của AA’ biến hình chóp A.A’B’C’D’ thành hình chóp A’.ABCD và phép đối xứng qua (BB’DD’) biến hình chóp A’.ABCD thành hình chóp C’.ABCD. Do đó, A.A’B’C’D’ và C’.ABCD bằng nhau (vì phép đối xứng qua mặt phẳng phép dời hình)
Cách 2: cho điểm O cố định. Phép biến hình biến mỗi điểm M trong không gian thành điểm M’ sao cho 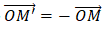
Gọi O là trung điểm của AC’ thì O cũng là trung điểm của các đường chép BD’, A’C, B’D nên phép đối xứng tâm O biến A, A’, B’, C’, D’ lần lượt thành C’, C, D, A, B. vậy các hình chóp A.A’B’C’D’ và C’.ABCD bằng nhau (do phép đối xứng tâm là phép dời hình).
b) Xét phép đối xứng qua mặt phẳng (ADC’B’)
Ta có: A->A';B->A,C->D,A'->B,B'->B; C'->C'
Do đó lăng trụ ABC.A’B’C’ -> lăng trụ AA’D’.BB’C’
Vì vậy hai lăng trụ ABC.A’B’C’ và AA’D’.BB’C’ bằng nhau.
• Phép tịnh tiến là phép dời hình.
Nếu phép tính tiến v→ biến hai điểm M, N lần lượt thành M’, N’ thì
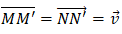
Suy ra M’N’ = MN hay phép tịnh tiến là một phép dời hình.
• Phép đối xứng trục là phép dời hình.
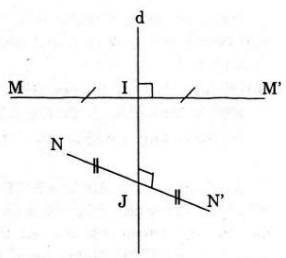
Cách 1. Gọi Đd là phép đối xứng qua đường thẳng d
Giả sử I là trung điểm MN’, J là trung điểm của NM’
Suy ra I, J ∈ d
Ta có:
Từ (1), (2), (3) suy ra MN2=MN'2=>MN=M'N'
=> Vậy phép đối xứng trục là phép dời hình.
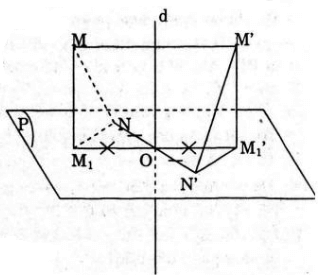
Cách 2. Giả sử phép đối xứng qua đường thẳng d biến M thành M’, N thành N’
Gọi (P) là mặt phẳng chứa NM’ và (P) // MM’
M1,M1' lần lượt là hình chiếu của M, M’ trên (P); O = ∩(P). Ta có d ⊥ (P) nên O đồng thời là trung điểm của M1 M1' và NN'. Vậy phép đối xứng tâm O biến M1 thành M1', N thành N’ nên M1 M1' nên M1 N=M1'N'.
Mặt khác M1 N,M1'N' lần lượt là hình chiếu của MN, M’N’ trên (P), MM’ // (P) nên MN = M’N’.
Vậy phép đối xứng qua đường thẳng là phép dời hình.
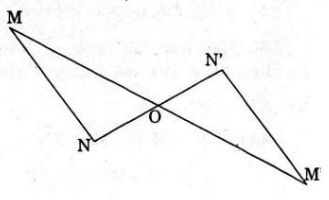
• Phép đối xứng tâm là phép dời hình.
Nếu phép đối xứng tâm O biến hai điểm M, N lần lượt thành M’, N’ thì
Vậy phép đối xứng tâm là phép dời hình.
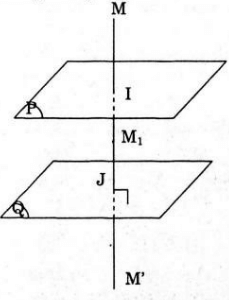
a) Lấy điểm M bất kì trong không gian
Giả sử phép đối xứng qua (P) biến M thành M1 và phép đối xứng qua (Q) biến M1 thành M’.
Gọi I, J là trung điểm của MM1, M1 M' (suy ra I ∈ (P), J ∈(Q), IJ ⊥ (P))
Ta có:
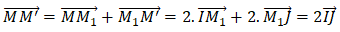
Chú ý rằng: IJ→ có phương vuông góc với (P) độ dài bằng khoảng cách giữa (P) và (Q)) hường từ (P) đến (Q)).
Nếu đặt 2IJ→= v→ thìv→ có phương, hướng và độ dài không đổi. Khi đó phép tịnh tiến theo X→ biến M thành M’. Vậy hợp thành 2 phép đối xứng qua hai mặt phẳng song song là một phép tịnh tiến.
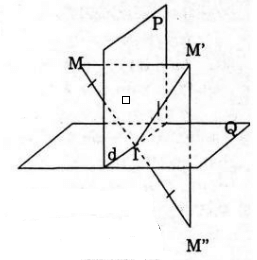
c) Gọi d = (P) ∩ (Q). M là một điểm bất kì. Giả sử phép đối xứng qua (P) biến M thành M’ và phép đối xứng qua (Q) biến M’ thành M’’.
I ∈ (P) và I ∈ (Q)
I ∈ d mà d ⊥ MM’’ (do d <=> (Q). Vậy d là đường trung trực của MM’’.
Trường hợp M ∈ (Q) nhưng M ∈ d tương tự.
Trường hợp 3. Nếu M ∈(P) và M ∈(Q) thì M, M’, M’’ phân biệt. Vì I = (P)∩ (Q) mà (P), (Q) lần lượt là mặt phẳng trung trực của MM’, M’M’’ nên d ⊥ (MM’M’’) => d ⊥ MM'' (*).
Mặt khác, gọi I là trung điểm của MM’’, do ΔMM’M’’ vuông tại M’ nên IM = IM’ = IM’’ => I đồng thời thuộc mặt phẳng trung trực của MM’ và M’M’’ hay I ∈(P) và I ∈(Q)=>I ∈d (**)
Từ (*), (**) ta có d là đường trung trực của đoạn MM’’ (3)
Kết luận: từ (1), (2), (3) ta thấy: nếu thực hiện liên tiếp hai phép đối xứng qua hai mặt phẳng vuông góc (P) và (Q) thì mỗi điểm M ∈ d (với d ∈(P)∩ (Q) biến thành chính nó, mỗi điểm M ∈d biến thành M’’ sao cho d là trung trực của MM’’. Đó chính là phép đối xứng qua đường thẳng d.
Hướng dẫn giải.
- Do phép vị tự biến ba điểm thằng hành thành 3 điểm thằng hàng nên nó biến đường thẳng a thành a’. Hơn nữa a’ song song hoặc trùng với a
Thật vậy, trên a lấy điểm A, B; Giả sử V0,k biến A thành A’ biến B thành B’.
Ta có:
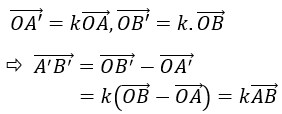
- Trường hợp 1: k = 1 và O ∈ a thì A’B’ = AB hay a = a’.
- Trường hợp 2: k ≠ 1 và O ∉ a thì A’B’ // AB hay a’ // a
Phép vị tự V0,k biến đường thẳng thành đường thẳng song song hoặc trùng với nó nên biến hai đường thẳng cắt nhau thành hai đường thẳng cắt nhau. Vậy nó biến mp(α) thành mặt phẳng (α'). Hơn nữa mp(α') song song hoặc trùng với mp(α). Thật vậy:
- Nếu O ∈ (α) thì V0,k biến A ∈(α) thành A’ sao cho OA'→=kOA→.
=> A'∈ OA hay A' ∈ mp(α) suy ra mp(α') = mp(α).
- Nếu k =1 thì V(O,1)(A) = A’ hay 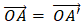
Vậy qua V(0,k) biến mp (α) thành mp(α') = mp(α).
- Nếu O ∈ mp(α) và k ≠ 1. Trên mp(α) lấy hai đường thẳng a, b cắt nhau tại I.
Qua phép vị tự tâm O tỉ số k :
+ Biến hai đường thẳng a, b thành 2 đường thẳng a’, b’ song song hoặc trùng với a,b
+ Biến giao điểm I thành điểm I’ là giao điểm của hai đường thẳng a’ và b’.
+ Biến mp (α) thành mp(α’) chứa hai đường thẳng a’và b’.
Suy ra, mp(α) // mp (α’).
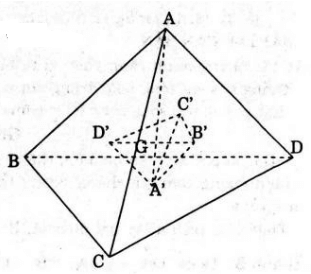
a) Gọi G là trọng tâm của tứ diện ABCD.
Gọi A’, B’, C’, D’ lần lượt là trọng tâm của các tam giác BCD, ACD, ABD, ABC.
Theo tính chất của trọng tâm tứ diện đều, ta có:
Nên V(G,-1/3) biến A, B, C, D lần lượt thành A’, B’, C’, D’
hay V(G,-1/3) biến tứ diện ABCD thành tứ diện A’B’C’D’ nên A’B’C’D’ là tứ diện dều.
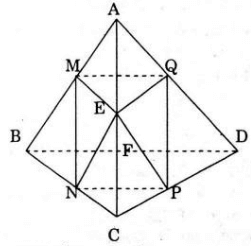
b) Xét tứ diện đều ABCD có độ dài cạnh là a. Gọi M, N, P, Q, E, F lần lượt là trung điểm của cạnh AB, BC, CD, DA, AC, BD.
* Xét tam giác ABC có M, E lần lượt là trung điểm của AB, AC
⇒ ME là đường trung bình của tam giác ABC nên
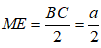
Chứng minh tương tự ta có:
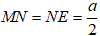
Suy ra, tam giác MNE là tam giác đều.
* Chứng minh tương tự, các tam giác ENP,EQP, EMQ, MNF, FNP, FQP, FMQ là các tam giác đều.
* Các mặt này tạo thành khối đa diện có các đỉnh M, N, P, Q, E, F mà mỗi đỉnh là đỉnh chung của 4 cạnh.
Vậy M, N, P, Q, E, F là các đỉnh của một khối 8 mặt đều.
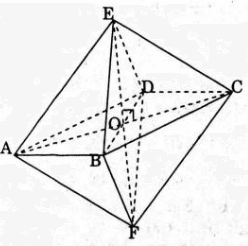
Xét khối 8 mặt đều ABCDEF cạnh a. Vì A, B, C, D cách đều E và F nên A, B, A, D cùng thuộc mặt phẳng trung trực của đoạn EF và do đó ABCD là hình thoi ( vì AB = BC = CD = DA)
Vì A, B, C, D cách đều E và F (EA = EB = EC = ED = FA = FB = FC = FD = a)
nên A, B, C, D cùng thuộc mặt phẳng trung trực của đoạn EF và ABCD là hình thoi (vì AB = BC = CD = DA = a)
a) Tứ giác ABCD là hình thoi nên AC và BD cắt nhau tại trung điểm O của mỗi đường.
Tương tự, AC và EF cắt nhau tại trung điểm của mỗi đường.
Vậy AC, BD, EF cắt nhau tại trung điểm của mỗi đường.
b) Tứ giác ABCD là hình thoi nên ta cũng có AC ⊥BD
Tương tự AC ⊥ EF, BD ⊥ EF.
Vậy AC, BD, EF đôi một vuông góc.
c) Cách 1. Dễ thấy ΔABD = ΔEBD (c-c-c) nên các trung tuyến tương ứng bằng nhau tức là AO = EO => AC = EF, tương tự, AC = BD.
Vậy AC = BD = EF (đpcm).
Cách 2. Vì EO ⊥ (ABCD) nên AO, OB là hình chiếu của EA, EB trên (ABCD)
Mà EA = EB ⇒ OA = OB ⇒ AC = DB.
Tương tự, AC = EF.
Vậy AC = BD = EF.
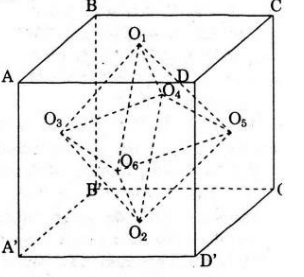
a) Xét khối lập phương ABCD.A’B’C’D’ cạnh a. Gọi O1, O2,O3,O4,O5,O6 lần lượt là tâm của các mặt phẳng ABCD, A’B’C’D’, ABB’A’, BCC’B’, CDD’C’, DAA’D.
Ta có: O1 là trung điểm của BD, O3 là trung điểm của A’B’ nên:
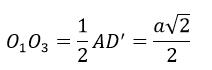
Tương tự: O1O4 = O1O5 = O1O6 = O3O4 = O4O5 = O5O6 = O1O6 = O3O4 = O4O5 = O5O6 = O6O3 = O2O3 = O2O4 = O2O5 = O2O6 = (a√2)/2
Do đó, các tam giác O1O3O6; O1O6O5; O1O5O4; O1O3O4; O2O3O6; O2O6O5; O2O5O4; O2O3O4 là các tam giác đều cạnh
Chúng làm thành khối tám mặt đều (đpcm).
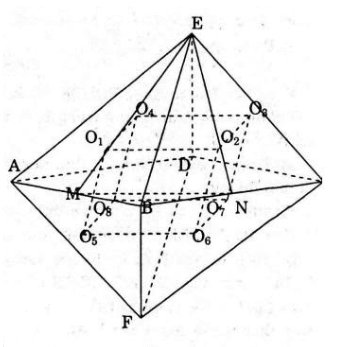
b) Xét khối tám mặt đều ABCDEF. Gọi O1, O2,O3,O4,O5,O6, O7, O8 lần lượt là trọng tâm của các mặt EAB, EBC, ECD, EDA, FAB, FBC, FCD, FDA.
- Gọi M, N lần lượt là trung điểm của AB, BC.
Ta có: O1,O2 là trọng tâm ΔEAB, EBC nên:
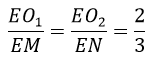
=> O1 O2 // MN
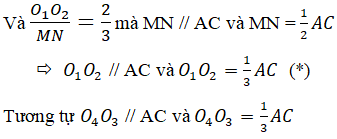
=> O1 O2 // O3 O4 và O1 O2 = O3 O4
=> Tứ giác O1 O2 O3 O4 là hình bình hành.
Lại có: O1 O4 // BD, O1 O4=BD/3 kết hợp (*) và lưu ý rằng.
AC = DB, AC ⊥ BD => O1 O2=O1 O4, O1 O2 ⊥ O1 O4 nên tứ giác O1 O2 O3 O4 là hình vuông.
- Hoàn toàn tương ứng ta có:
O1 O2 O6 O5,O2 O3 O7 O6,O3 O4,O8 O7,O4 O1 O5 O8,O5 O6 O7 O8 là các hình vuông.
Vậy O1, O2,O3,O4,O5,O6, O7, O8 là các đỉnh của một khối lập phương.













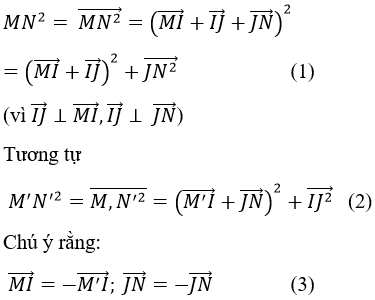
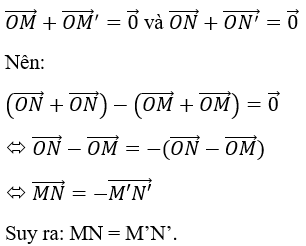








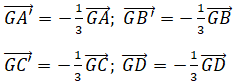


NTH_AT_12 đã đọc và hiểu!
Trả lờiXóaNTH_AT_17 đã đọc và hiểu
Trả lờiXóaNTH-AT-05 đã đọc và hiểu
Trả lờiXóaNTH-AT-11 đã đọc và hiểu
Trả lờiXóa